#寻找真知派#
上一篇文章讲述了如何进行正态分布检验。今天我们来看一下日常统计分析和预测为什么要求误差和残差必须服从正态分布。
首先我们先明确一下误差和偏差的概念。
误差(Error)是指观测值和真实值之间的偏差,误差越大,说明观测或测量不准确。误差可以分为系统误差和随机误差两种。系统误差指受试验条件和人为因素引发的偏差,比如仪器刻度不准确产生的偏差。系统误差具有规律性和可重复性,因此其误差样本的分布往往呈现明显的偏态特征,不会服从正态分布。如果我们观测到误差不服从正态分布,就可以大概率判断出现了系统误差,可以通过改善试验条件消除或减小系统误差。(奸商对磅秤做手脚,短斤少两就是系统误差)。
随机误差也称为偶然误差和不定误差,是由于在测定过程中一系列有关因素微小的随机波动而形成的具有相互抵偿性的误差,比如一会偏差变大,一会又变小,完全随机,毫无规律,因此随机误差很难避免切不可干预。根据中心极限定理,多种独立因素引发的随机现象的总和在大量采样后接近正态分布。由于随机误差的影响因素很复杂,因此在理论和实践中,误差是否正态分布是随机误差的判定标准。如果判定误差属于随机误差并且误差水平在可以承受的范围之内,则可接受试验的结果。如果是随机误差但误差水平太高,则说明产品质量极难保障,生产过程干扰因素太多太强烈且很难消除。
残差(Residual)特指预测值与真实值之间的偏差,常用来评价一个预测模型的准确水平。残差可以看做是误差的特例。因此如果残差不服从正态分布,说明样本数据中还有规律性的信息没有被当前模型发掘出来,模型需要继续改进,进一步提取数据中隐藏的规律,直到残差符合正态分布为止。这就是为什么在预测领域进行模型检验要求残差必须服从正态分布的原因。
以下我们看一个预测的例子。下图为个人收入和信用卡贷款额度的两个预测模型,其中1个为线性回归模型,另一个为二阶多项式回归模型。
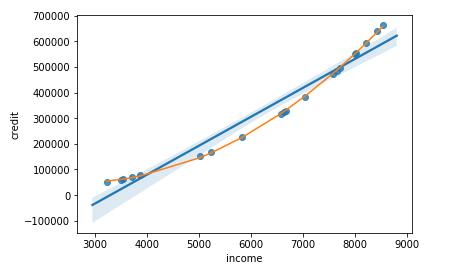
信贷预测模型
两个预测模型的残差分布如下所示。
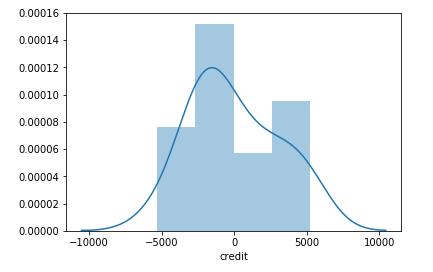
多项式预测模型残差分布
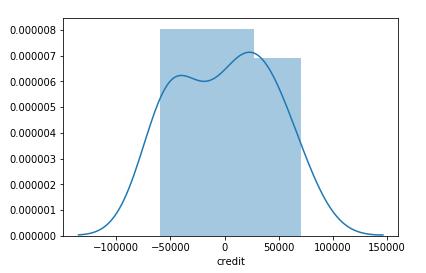
线性回归预测模型残差分布
从上述两个预测模型的残差分析来看,二阶多项式预测模型的残差水平更低且正态分布特征更加明显,通过正态分布检验,其显著水平(p=0.5)也远高于线性回归模型(p=0.09)。因此二阶多项式预测模型预测效果更好。
#技术技能超级玩家#






 本文探讨了误差和残差在统计分析中的作用,强调了它们需服从正态分布的原因。系统误差和随机误差分别解释,并指出随机误差在大量采样后趋向正态分布。残差作为模型预测精度的指标,其正态分布是模型完善的关键。文中通过线性回归和二阶多项式回归模型的比较,展示了正态分布残差对于模型预测性能的重要性。
本文探讨了误差和残差在统计分析中的作用,强调了它们需服从正态分布的原因。系统误差和随机误差分别解释,并指出随机误差在大量采样后趋向正态分布。残差作为模型预测精度的指标,其正态分布是模型完善的关键。文中通过线性回归和二阶多项式回归模型的比较,展示了正态分布残差对于模型预测性能的重要性。
















 1466
1466

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








