抛物线中四边形面积最大值_「解题策略」面积系列之四边形面积

除了关于三角形的各种面积问题之外，四边形问题也是中考题中常见的一种问法，鉴于四边形一般是普普通通的四边形，因此问题一般也是普普通通的问题，本文分享一点关于四边形面积的题目．

拆解四边形

如何求一个普通的四边形的面积？

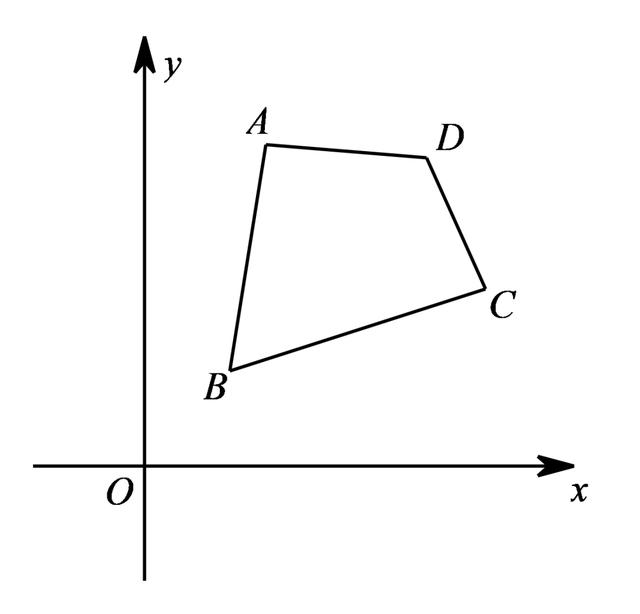
解法也很普通，连对角线分割为两个三角形即可求得面积．至于三角形面积参考前文铅垂法．

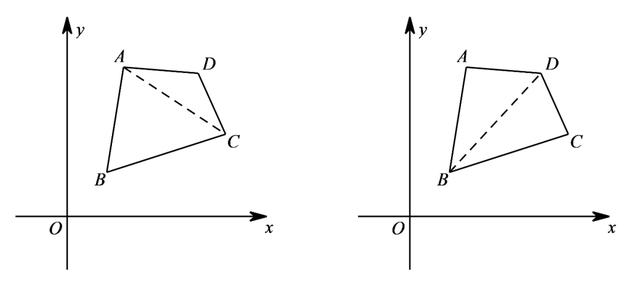
搞定了四边形的面积，就可以看看四边形面积的最值了，还是来看点例子吧：

2019东营中考(删减)

已知抛物线y=ax²+bx-4经过点A(2,0)、B(-4,0)，与y轴交于点C．

(1)求这条抛物线的解析式；

(2)如图，点P是第三象限内抛物线上的一个动点，当四边形ABPC的面积最大时，求点P的坐标；

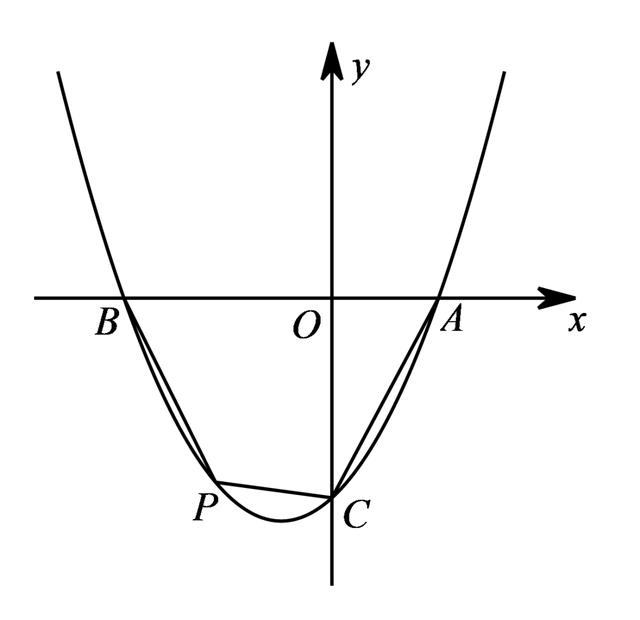
【分析】

(1)y=0.5x²+x-4；

(2)此处四边形ABPC并非特殊四边形，所以可以考虑连接对角线将四边形拆为两个三角形求面积．

若连接AP，则△ABP和△APC均为动三角形，非最佳选择；

若连接BC，可得定△ABC和动△BPC，只要△BPC面积最大，四边形ABPC的面积便最大．

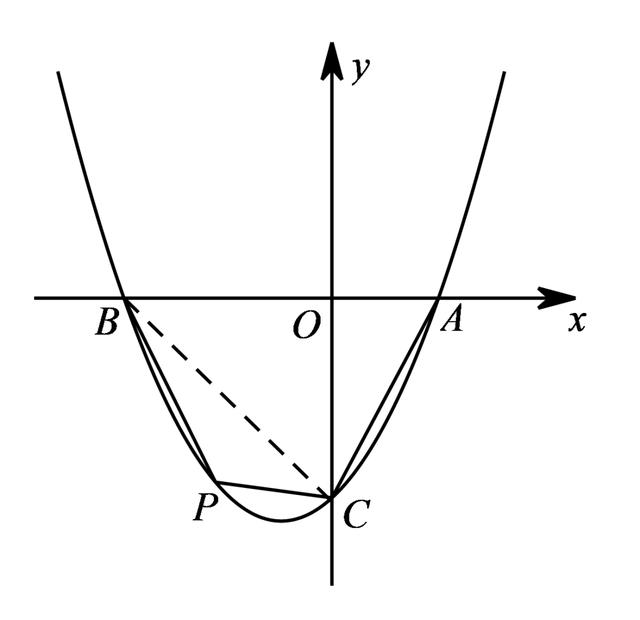
考虑A(2,0)、B(-4,0)、C(0，-4)，