常微分方程第三版_常微分方程：（第六章）非线性微分方程：4节

参考《常微分方程》第三版（王高雄）

第1、2节：juliar：常微分方程：（第六章）非线性微分方程：1、2节

第3节：juliar：常微分方程：（第六章）非线性微分方程：3节

讨论平面非线性微分方程组解的全局图貌，给出相平面上极限环的存在性判断方法和相平面轨线图貌画法。——6.4

6.4 极限环和平面图貌

6.4.1 极限环

极限环：孤立的周期解（闭轨线），在相平面上称为极限环。（p295）[孤立：意味着邻近的轨迹不是闭的，它们盘旋着接近或远离极限环][本质上是非线性现象，它们不能发生在线性系统中]

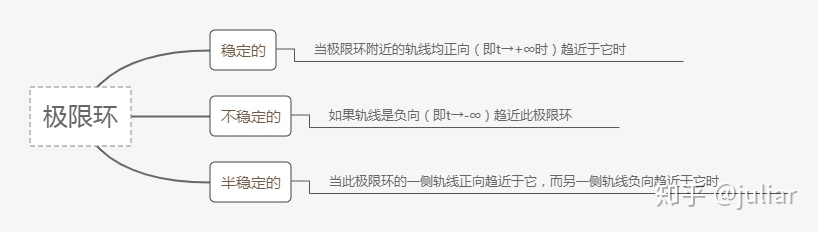
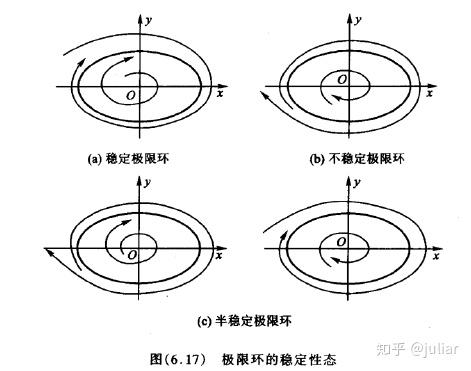
主要内容：

寻求极限环的方法：

（1）求出特解；

（2）本迪克松方法（参见第一节补充知识）—构造特殊的环域来寻求极限环（依据定理8）

极限环不存在定理（定理9）：通过构造具有别的特殊性质的域来否定周期解（极限环）的存在。

对某类型方程讨论如何确定极限环及其稳定性态的问题有重要意义，范德波尔方程、李纳微分方程（定理10：表明在对f和g适当的假设下，系统有唯一的稳定极限环）

主要定理：

范德波尔方程：

李纳微分方程：

定理10中

的假设理解：这个结果是合理的。对

的假设意味着回复力的作用像一个弹簧，趋向于位移的减缓，然而对

的假设意味着当

很小时，阻力是负的，当

很大时，阻力是正的。因为小振荡被激起且大振荡被压制，所以系统往往会进入一个自我维持的一些中间振幅的振荡也就不足为奇了。《非线性动力学与混沌》

6.4.2 平面图貌

相平面上两种特殊的轨线——奇点、极限环。

对于画一般的轨线图貌，一种是画方向场，另一种是等倾斜法。

定义回顾（p19）

• 方向场（向量场）、等倾斜线（等斜线）

• 垂直等倾斜线、水平等倾斜线

应用：可以运用上述等倾斜线法分析1.1中例5的两种群模型（6.52）和2.1.1中例2，得到以下定理：

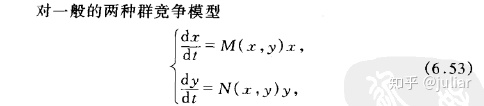
分界线：在相平面分析中除奇点和极限环两种特殊轨线外，还有一种从奇点到奇点的轨线，这类轨线称为分界线。

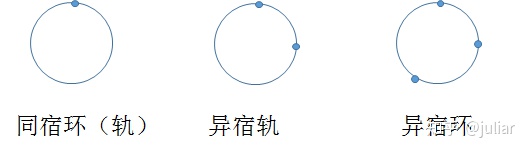
同宿环（轨）：如果一条分界线与一个奇点构成一个环，则称为同宿环（轨）

《非线性动力学与混沌》同宿轨：把出发点和终点都为同一不动点的轨道，称为同宿轨。当

时，轨迹都逼近原点。

异宿轨：如果一条分界线两端是不同奇点，则分界线称为异宿轨

《非线性动力学与混沌》异宿轨：成对的鞍点被一对轨迹连接起来，它们被叫做异宿轨道。

异宿环：当多条分界线与多个奇点构成一个环时则称此环为异宿环

上述定义中可以将奇点换为极限环。

拓扑等价：如果两个常微分方程的所有解之间存在一对一的对应（同胚）关系，且保接轨线定向，则可称这两个常微分方程是拓扑等价的.

结构稳定：给定了一个平面驻定常微分方程，对与之非常接近的所有平面驻定常微分方程，可以用相平面上的点的向量非常接近来表示，如果它们是拓扑等价的，则称给定的常微分方程是结构稳定的。

结构稳定的充要条件：数学家安德罗诺夫（Andronov）和庞特里亚金（Pon-tryagin）曾给出：

---

matlab解微分方程、绘制轨线图：

1.编写微分方程组的M文件，保存文件名为odefile.m。（注意要保存在当前matlab执行的文件夹下）

参考matlab怎么调用自定义函数

function dy=odefile(t,y,p1,p2)
dy=[f1;f2;...;fn]

2.调用微分方程数值函数

[T,Y]=ode45('odefile',[a,b],y0)

其中ode45为龙格-库塔（4，5）法，其他有：

ode23龙格一库塔（2，3）法；

ode113多步 Adams-Bashforth-Moulton法.

%积分曲线图：
plot(T，Y(：，1)，’-r’，T，Y(：，2)，'.g’)
%轨线图：
plot(Y(：，1)，Y(：，2)，'-r')

3.绘制向量场与等高线图

%向量场：
quiver（x，y，u，v）向量起始点和终点坐标；
quiver3（x，y，z，u，v，w）向量起始点和终点坐标。
%等高线图：
contour（X，Y，Z，m）绘制m条等高线平面图；
contour3（X，Y，Z，[a，b]）绘制Z在[a，b]范围的等高线立体图.

p398例4：解微分方程

• 首先编写要调用的ode1.m文件

function dy=ode1(x,y)
dy=[1;1-y(2)^2];

• 绘制轨线图

clear 
c=0.01;
x0=-3.1:0.2:3.;
y0=-3.:0.2:3.1;
[x,y]=meshgrid(x0,y0); 
d=sqrt(1+(1-y.^2).^2);
u=c./d;
v=c*(1-y.^2)./d;
hold on
quiver(x,y,u,v)
hold off
[X,Y]=ode45('ode1',[-3,3],[-3;-0.99]);
>> hold on
>> plot(X,Y(:,2),'-r')
>> hold off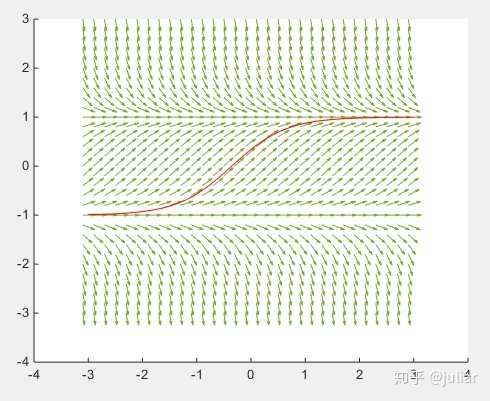

p399例5：哈密顿函数

的轨线图（等势图）

clear
[X,Y]=meshgrid(-2:.1:2); 
Z=Y.*Y/2-X.*X/2+X.^4/4; 
>> mesh(X,Y,Z)
hold on 
contour(X,Y,Z)
hold off 
hold on 
contour3(X,Y,Z)
hold off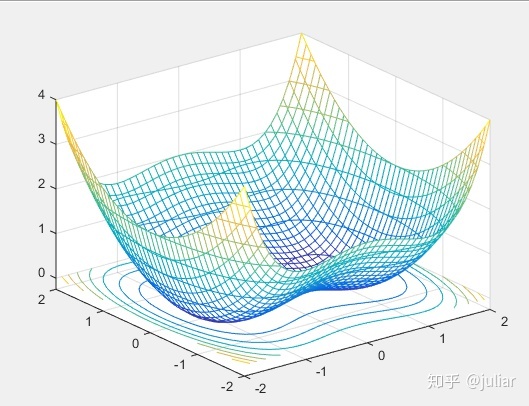

p399例6：V函数

的等高线图及微分方程

的轨线图。

• 先编写fexa6.m

function dx=fexa6(t,x)
dx=[x(2);-2*x(1)-3*x(2)];

• 绘制轨线图

clear
[X,Y]=meshgrid(-10:.1:10); 
Z=(8*X.*X+4*X.*Y+Y.*Y)/2; 
hold on 
contour(X,Y,Z,[0.2 13 8 15 2540 80 200 500 1000])
axis([-10 10 -10 10])
hold off
[T,X]=ode45('fexa6',[0 20],[-10;10]); 
hold on 
plot(X(:,1),X(:,2),'-r')
hold off
[T,X]=ode45('fexa6',[0 20],[-8;-10]); 
hold on 
plot(X(:,1),X(:,2),'-g')
hold off
[T,X]=ode45('fexa6',[0 20],[8;10]);
hold on 
plot(X(:,1),X(:,2),'-r')
hold off
[T,X]=ode45('fexa6',[020],[8;-10]); 
hold on 
plot(X(:,1),X(:,2),'-g')
hold off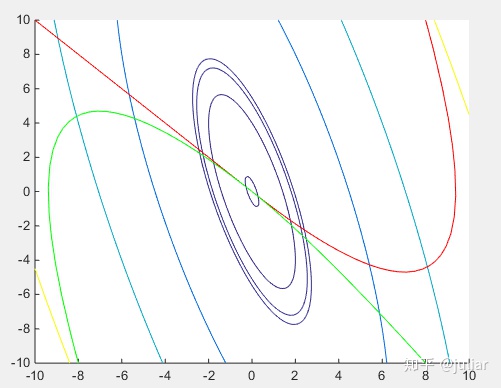

——————————————————————————————————————

Matlab绘制极限环

参考：

Chenglin Li：非线性系统（一）极限环​zhuanlan.zhihu.com

参考列表 - MATLAB & Simulink - MathWorks 中国​ww2.mathworks.cn

1.稳定极限环

实例：p294例1

streamslice(x,y,f1,f2) f1、f2是x、y的函数方程组，streamslice表示以适中的间距绘制一族带箭头的流线图；
meshgrid用于生成网格数据

[x,y]=meshgrid(linspace(-2,2,100));
streamslice(x,y, x+y-x.*(x.^2+y.^2), -x+y-y.*(x.^2+y.^2));
axis([-2,2,-2,2])
grid on
xlabel('x')
ylabel('y')
title('Limit Circle')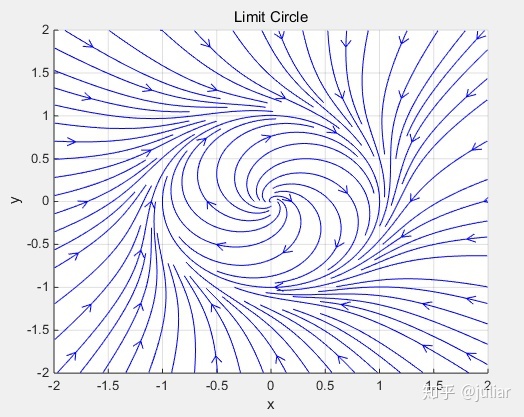

2.不稳定极限环

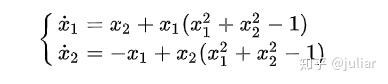
[x1,x2]=meshgrid(linspace(-2,2,100));
    streamslice(x1,x2, x2+x1.*(x1.^2+x2.^2-1), -x1+x2.*(x1.^2+x2.^2-1));
    axis([-2,2,-2,2])
    grid on
    xlabel('x1')
    ylabel('x2')
    title('Limit Circle')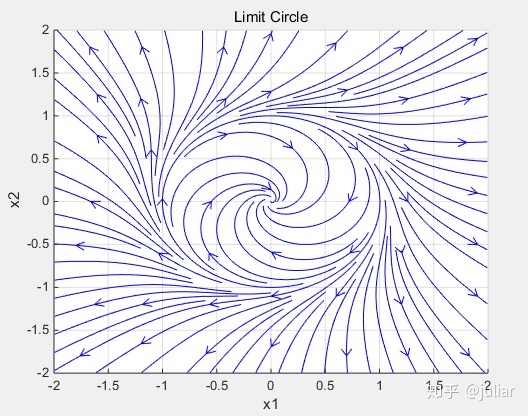

3.半稳定极限环

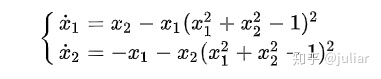
[x1,x2]=meshgrid(linspace(-5,5,100));
    streamslice(x1,x2, x2-x1.*(x1.^2+x2.^2-1).^2, -x1-x2.*(x1.^2+x2.^2-1).^2  );
    axis([-5,5,-5,5])
    grid on
    xlabel('x1')
    ylabel('x2')
    title('Limit Circle')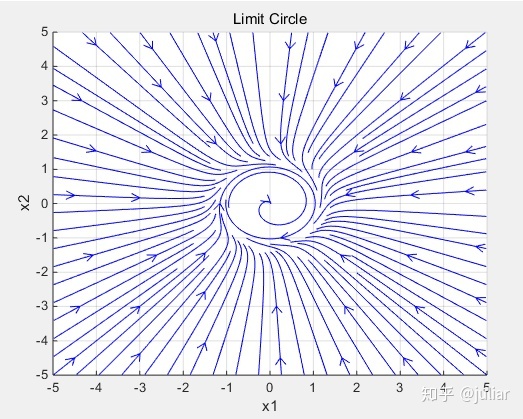

2020.11.24