双目标帕累托优化_多目标优化(八): 多任务之连续帕累托解

八. 连续帕累托解

参考文献：Ma, Pingchuan, Tao Du, and Wojciech Matusik. "Efficient Continuous Pareto Exploration in Multi-Task Learning." arXiv preprint arXiv:2006.16434 (2020).

1. 主要思想

前面我们介绍了单个帕累托解和多个帕累托的求解方法，接下来我们介绍一种能够输出局部连续帕累托解，进一步构建帕累托前沿(Pareto Front)的方法[11]。分如下的两步：

• 离散帕累托求解(本文第4部分): 给定初始点，在求出一个帕累托平稳点后，从过点的平滑曲线切线出发，进行次搜索：计算搜索方向，扩展出平稳点；
• 连续帕累托解(前沿)构建(本文第5部分)：由初始点及 扩展出的平稳点集，构建出连续帕累托前沿。

为表述方便，这里引用论文中关于多任务学习的定义：

设光滑，

2. 预备知识：Krylov子空间[12]

这一节内容参考潘建瑜老师《线性方程组迭代方法》课程，第四讲 《Krylov 子空间方法 》[12]

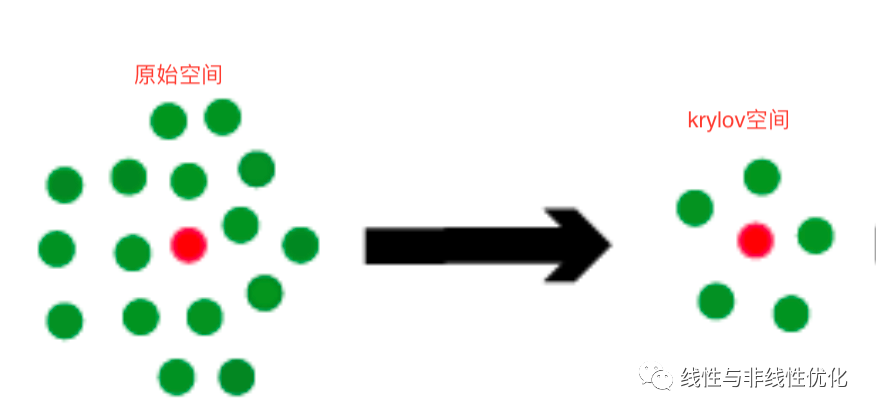
大规模稀疏线性方程组 求解的首选方法是Krylov 子空间方法，其基本思想是在一个维数较小的子空间  中寻找近似解.

Krylov 子空间定义：设 ,  ,我们称

是由 和  生成的 Krylov 子空间， 通常简记为 。Krylov 子空间有如下的3个性质：

• Krylov 子空间嵌套性：；
• 的维数不超过m；
• 为次数小于m的多项式。

简单来说，通过求解Krylov 子空间的解来近似原始线性方程组的解。

3. 基本概念

定义1：帕累托平稳点(Pareto Stationary) : 设连续可微，点称为帕累托平稳点，如果存在， 使得下式成立：

引理2 ：帕累托点都是帕累托平稳点。

引理3 ：设是光滑且是帕累托点，是过点的曲线：

则存在 使得：

其中，为切线

上式表明，算子将点处的切向量变换为由扩张成的子空间(Krylov子空间)的向量。 

4. 离散帕累托求解

给定初始点,光滑，可以从如下三步来获取连续帕累托解：

• 求解帕累托平稳点: 从初始点出发，通过梯度下降的方法求解帕累托平稳点
• 扩展帕累托平稳点：在点处光滑，如果帕累托前沿存在，则在点处的某个邻域内存在着帕累托平稳点。由此出发，可以求得一系列的帕累托平稳点；
• 将上述的平稳点所在的局部帕累托前沿进行连接合并，扩充成更大的连续帕累托前沿。

• 

我们先来看下如何获取一系列的帕累托平稳点。

4.1 梯度求解方法

这里可以通过前面介绍的梯度求解算法，参考笔者往期文章:

多目标优化(四): 梯度下降算法

多目标优化(七): 多任务之多个帕累托解

4.2 一阶方法扩张

通过梯度求解方法求解出帕累托平稳点后，可以基于该点扩展出局部帕累托集(目标函数光滑)。这一过程可以分解为两步：

• 1).计算：计算式中的;
• 2).求解搜索方向: 估计梯度迭代的搜索方向。

有了搜索方向，可以通过如下更新公式求解：

我们先来看第一步。

1).计算

计算可以归结为求解如下的约束问题：

上述问题规模为,量级较小，可以很方便的求解出来。

2).求解搜索方向

求解得到后，由引理3，我们可以给出待求解的线性方程组：

其中为待求解的变量。上述问题求解有两个难点：

• 不一定是帕累托平稳点
• 问题的复杂度是 ,当n非常大时，求解起来非常困难。

为此引入校正向量(correction vector),将改写为：

式引入了校正向量(correction vector) ,用近似，将会是帕累托平稳点。

引理4：设是问题的解，则问题的解是:

在计算出、帕累托平稳点、校正向量，可以计算出。现在考虑如下的稀疏线性方程组：

为随机生成的向量，为待求解的变量。式可以通过krylov子空间，MINERS方法进行求解。详细MINERS算法可以参考潘建瑜老师《线性方程组迭代方法》课程，第四讲 《Krylov 子空间方法 》[12]

我们来看下寻找离散帕累托解集合的求解算法，如下图所示：

随机初始化网络，输出N个帕累托平稳网络。

• 输入：随机初始化网络
  • 生成点的个搜索方向;由个搜索方向扩展出个子网络；
  • 更新子网络节点：；
  • 输出帕累托平稳点。
• 输出：N个帕累托平稳网络

5. 连续帕累托解(前沿)构建

通过前面的Algorithm 1求解出来N个帕累托平稳网络(父节点及K个子网络)；接下来介绍如何由离散的帕累托点合并成更大的连续帕累托前沿(Front)。

给定及其对应的K个子节点,定义连续变量 以及搜索方向：

点处的局部帕累托集可以通过下式进行构建：

是由点及对应的K个子节点构成的凸包；切平面中切向量的线性组合仍然在切平面。

对于N个局部帕累托集：

可以将两两接壤处合并成一个更大的局部帕累托集合，全部合并完后，就可以生成多个的连续帕累托前沿(Front)。

参考文献

• [1] [贺莉，刘庆怀 著。《多目标优化理论与连续化方法》。2015-06。科学出版社 ]
• [2] [陈宝林 著。《最优化理论与算法》(第2版)。2005-10。清华大学出版社 ]
• [3] [KKT条件，Karush–Kuhn–Tucker conditions,https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions ]
• [4] [约束规格，constraint qualifications ,https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions#Regularity_conditions_(or_constraint_qualifications) ]
• [5] [S.D. Sudhoff.  Lecture 9:Multi-Objective Optimization,https://engineering.purdue.edu/~sudhoff/ee630/Lecture09.pdf ]
• [6] [Fliege, J., Svaiter, B. Steepest descent methods for multicriteria optimization. Mathematical Methods of OR 51, 479–494 (2000). https://doi.org/10.1007/s001860000043 ]
• [7] [Désidéri, Jean-Antoine. "Multiple-gradient descent algorithm (MGDA) for multiobjective optimization." Comptes Rendus Mathematique 350.5-6 (2012): 313-318. ]
• [8] [ Gebken, Bennet, Sebastian Peitz, and Michael Dellnitz. A descent method for equality and inequality constrained multiobjective optimization problems. Numerical and Evolutionary Optimization. Springer, Cham, 2017.]
• [9]  Sener, O. and Koltun, V. Multi-task learning as multi- objective optimization. In Advances in Neural Informa- tion Processing Systems, pp. 527–538, 2018.

• [10] Lin, X., Zhen, H.-L., Li, Z., Zhang, Q.-F., and Kwong, S. Pareto multi-task learning. In Advances in Neural Information Processing Systems, pp. 12037–12047, 2019.

• [11] Ma, Pingchuan, Tao Du, and Wojciech Matusik. "Efficient Continuous Pareto Exploration in Multi-Task Learning." arXiv preprint arXiv:2006.16434 (2020).

• [12] 潘建瑜《线性方程组迭代方法》课程，第四讲 《Krylov 子空间方法 》http://math.ecnu.edu.cn/~jypan/Teaching/MatrixIter/lect04_Krylov_ssm.pdf