matlab有限域多项式除法_代数Artin(十五): 域

——————————————— 完更撒花~（10/10）——————————————

[参考文献] Michael Artin: Algebra (2nd Edition)

1 域的例子

[域扩张] 给定一对域

,

称为

的一个域扩张，或扩域。

• 记号
  表示
  是
  的域扩张。

[数域] 数域

是

的一个子域。

• 的任何子域都包含
  有理数域
  ，所以数域是
  的域扩张。
• 最常被研究的数域是代数数域，其所有元素都是代数数。

[有限域] 有限域是包含有限个元素的域。

• 一个有限域包含一个素域
  ，因此它是那个素域的域扩张。

[函数域] 有理函数域

的扩张称为函数域。

• 函数可以用方程
  定义，其中
  是不可约复多项式，变量为
  和
  .

---

2 代数元和超越元

[代数元] 令

是域

的扩张，令

是

的元素，

是

上的代数元，如果

是系数在

上的首一多项式的根，比如：

.

[超越元] 一个元素是

上的超越元，如果它不是

上的代数元——即如果它不是任何这种多项式的根。

上的所有元素都是

上的代数元，因为它是多项式

的根。

• 替换同态
  ，
  ，如果
  是单射，那么
  是超越元，如果
  不是单射，即核非零，那么
  是代数元。

[命题1---

在

上的既约多项式]

令

是

的扩域，

是

上的代数元。以下关于系数在

中的首一多项式

的条件是等价的。满足这个条件的唯一的首一多项式称为

在

上的既约多项式。

• 是
  中以
  为根的，次数最低的首一多项式。
• 是
  的既约元，且
  是
  的根
• 的系数在
  中，
  是
  的根，且
  的由
  生成的主理想是极大理想。
• 是
  的根，且如果
  是
  中的任意以
  为根的多项式，那么
  整除
  .

[

在

上的次数]

在

上的不可约多项式的次数称为

在

上的次数。

[由

生成的子域]

令

是

的扩域，

由元素

生成的子域记为

:

是包含

和

的

的最小子域。

• 类似地，
  是包含
  和
  的
  的最小子域

[由

生成的环]

上由元素

生成的环记为

。

• 它是
  的像，它的元素可以由系数在
  中变量为
  的多项式
  组成：
• 域
  和
  的分式域同构。
• 类似地，如果
  ，
  的包含
  和这些元素的最小环记为
  ，它由
  的元素
  组成，
  可表示为系数在
  中变量为
  的多项式，
• 域
  是环
  的分式域。
• 如果
  是
  上的超越元，那么
  是同构，
  与有理函数域
  同构。对于所有的超越元
  所有域扩
  都是同构的。

[命题2---代数元生成的环域相等] 令

是域扩

的元素，它是

上的代数元，令

是

在

上的既约多项式，

1. 典范映射
   是同构，且
   是域，因此
2. 更一般地，令
   是扩域
   的元素，且是
   上的代数元，那么环
   与域
   相等。

证明：(1) 令

是替换映射

，因为理想

是极大理想，

生成核，且

与

的像

同构。另外因为

是域，因此

是域。因为

是

的分式域，所以

。

(2) 由归纳：

[命题3---通过次数确定基] 令

是

上的代数元，且令

是

在

上的既约多项式。如果

的次数为

，即如果

在

上的次数为

，那么

是

上的向量空间

的基。

[命题4---相等的既约多项式] 令

是域，

是域扩

和

的元素。设

是

上的代数元。存在域的同构

是

上的恒等映射

，当且仅当

和

在

上的既约多项式是相等的。

证明： 因为

是

上的代数元，

，类似地，

, 假设两个元素的既约多项式都等于

，那么由命题2存在同构:

和

要证的同构

是复合映射

。

反过来，如果存在一个同构

是

上的恒等映射，且将

映为

，且如果

是系数在

的多项式使得

，那么同样

。所以这两个元素的既约多项式相等。

[定义---域扩张的同构] 令

和

是同一个域

的扩张，一个同构

，如果它在子域

上的限制是恒等映射，那么它称为

-同构，或域扩张的同构。

• 如果存在
  -同构
  ，那么
  和
  称为同构的扩域。

[命题---根的像也是根] 令

是

的域扩张的同构，令

是系数在

上的多项式。令

是

在

上的根，且令

是它在

上的像，那么

也是

的根。

证明： 假设

，因为

是

-同构且因为

，所以

. 因为

是同态，所以

因此

是

的根。

---

3 扩域的次数

[扩域的次数] 域

的扩张

，当被看作是

-向量空间时，

的维数称为扩域的次数，记为

• 次数是域扩张的基本性质

例：

有

-基

，因此次数

[有限扩张] 域扩张

称为有限扩张，如果它的次数是有限的。

• 次数为
  的扩域称为二次扩域（quadratic），次数为
  称为三次扩域（cubic）。

[引理---次数为1的情况]

1. 一个扩域
   次数为
   ，当且仅当
   。
2. 扩域
   的元素
   在
   上次数为
   ，当且仅当
   是
   的一个元素。

证明：如果

作为

上的向量空间维数为

，那么

的任何非零元都是一个

-基，如果

是基，那么每个

的元素都属于

。

由定义，

在

上的次数是既约多项式的次数，如果为

，那么多项式就是

，如果

有属于F的系数，那么

属于

。

[命题---添加平方根可得到二次扩域] 假设域

的特征不为

，即在

中

。那么

的任何二次扩域

都可以通过添加一个平方根得到：

, 其中

反之，如果

属于

的扩域，且

但

，那么

是

的二次扩域。

证明：首先证明每个二次扩域

都可以通过添加，系数在

内的二次多项式

的根得到。我们选择元素

,

，那么

是

上的线性不相关集合。因为

作为

上的向量空间维数为

，所以这个集合是

的一组基。因此

是

的系数在

中的线性组合，

，那么

是f(x)=x^2+bx+c 的根，因为

，所以这个多项式在

上是既约的。

多项式

的判别式是

。在特征不为

的域中，二次公式

可以解方程

。平方根有两种情况，令

是其中一个，那么

,

，又因为

，所以

在

上生成

。反之，如果

,但

，那么

是

的

-基，所以

.

[命题---代数元所在扩域的次数]

1. 如果扩域的元素
   是
   上的代数元，那么
   的次数
   等于
   在
   上的次数。
2. 一个扩域的元素
   是
   上的代数元，当且仅当次数
   是有限的。

证明： 如果

是

上的代数元，那么由定义，它的次数等于它在

上的不可约多项式

的次数。如果

的次数为

, 那么

有

-基

，所以

。

如果

不是代数元，那么

和

在

上的维数是无限的。

[定理---次数的乘法性质] 令

是域，那么

因此

和

都整除

证明：令

是

作为

-向量空间的基，令

是

作为

-向量空间的基。所以

且

。需证明

个乘积的集合

是

作为

-向量空间的基。当次数无限时推导类似。

令

, 因为

是

在

上的基，所以

可以唯一地表示成的

，系数

。因为A是K在F上的基，所以每个

可以唯一地表示成

，系数

那么

这表明

张成作为

-向量空间的

。如果这个组合为零，那么

为零

，即

为零

，所以

是不相关的，所以它是

在

上的基。

[推论1]

1. 令
   是次数为
   的有限扩域，且令
   ，那么
   是
   上的代数元，且它在
   上的次数整除
   .
2. 令
   是域，如果元素
   在
   上是代数元，那么它在
   上是代数元。如果
   在
   上的次数为
   ，那么它在
   上的次数最多是
   。
3. 一个由
   上有限多个代数元生成的扩域
   是一个有限扩张，一个有限扩张由有限个元素生成。
4. 如果
   是
   的扩域，那么
   中是
   上的代数元的元素组成
   的一个子域。

证明：(1) 元素

生成中间域

，由乘法性质有

，因此

是有限的，且整除

(2) 令

是

在

上的不可约多项式，因为

，

也是

的元素，因为

是

的根，所以

在

上的不可约多项式

整除

，所以

的次数最多等于

的次数。

(3) 令

生成

，且是

上的代数元。令

是由前

个元素生成的域

。这些域形成一个链

, 因为

在

上是代数元，所以它在更大的域

上也是代数元，因此次数

对于每个

都是有限的。由乘法性质，

是有限的。

(4) 需证明如果

是

的在

上是代数元的元素，那么

等也是

上的代数元。这可以从(1)(3)中得到，因为他们是域

的元素。

[推论2] 令

是

的次数为素数

的扩域，如果元素

不属于

，那么

在

上的次数为

，且

[推论3] 令

是域F的扩域，

和

是

的子域，也是

的有限扩张。令

是

的由

和

生成的子域，令

，那么

和

整除

，

证明：乘法性质说明

整除

。假设

由一个元素在

上生成：

，那么

，

在

上的次数等于

不超过

在

上的次数

。乘法性质表明

. 由多个元素生成的情况可以通过一次添加一个元素，归纳证明。

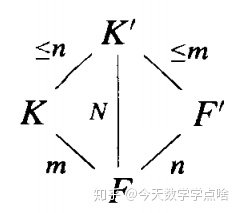
如果

互素，那么

---

4 求既约多项式

[引理---求

的多项式]

1. 元素
   的幂之间的一个线性相关关系
   意味着
   是多项式
   的根。
2. 令
   和
   是域
   的扩张中的代数元，且令他们在
   上的次数为
   。共
   个单项式

张成作为

-向量空间的

证明：(2) 因为

和

是

上的代数元，所以

，单项式们列出了

.

• 引理表明：给定
  的既约多项式，就可以知道以
  为根的多项式，但是这个多项式可能不是既约的。
• 在
  上的既约多项式是次数最低的以
  为根的多项式，为了确定这个既约多项式，需要知道
  在
  上的一组基，即如果
  是无关的，那么得到的
  的多项式就是既约的。

---

5 尺规作图

证明无法仅通过尺规作图将任意角三等分。

[尺规作图]

1. 给定平面两点，这些点是构造的（constructed）。
2. 如果两个点
   已被作出，我们可过他们画一条直线，或以
   为 圆心画一个过点
   的圆。这样的线和圆是构造的。
3. 已作出的圆和直线的交点是构造的。

基本的作图：点到直线的垂线，直线的平行线，在直线上标注长度。

[可构造的] 点，线，圆称为可构造的，如果他们可以按以上规则通过有限多步得到。

[命题---点坐标所在的域]

1. 令
   是坐标
   在实数域
   内的点，过
   的直线由系数属于
   的线性方程定义。以
   为中心过
   的圆由系数属于
   的二次方程定义。
2. 令
   是由线性方程定义的直线或由二次方程定义的圆，方程的系数属于实数域
   ，那么
   的交点的坐标属于
   ，或属于
   的实二次扩域
   .

[定理---可构造点的坐标] 令

是可构造的点。对于某整数

，存在域的链

, 使得：

• 是实数域的子域
• 的坐标属于
• 对每个
  ，次数
  等于
  .

因此次数

是

的幂。

[可构造的实数] 我们称一个实数

是可构造的，如果点

是可构造的。

• 因为可以通过尺规作图标注长度，所以实数
  是可构造的，当且仅当存在一对可构造的点
  之间的距离为
  。

[推论---可构造实数的次数] 令

是可构造的实数，那么

是代数数，且它在

上的次数是

的幂。

[可构造的角] 角

是可构造的，如果可以构造两条直线夹角为

• 如果在其中一条线上标注单位长度，并向另一条直线作垂线，那么就构造出了
  。反过来，如果
  是可构造实数，那么我们可以通过逆过程得到夹角为
  的两条直线。

[引理---20度角不可能作出] 实数

是

上的代数元，且它在

上的次数为

. 因此

不是可构造数。

• 因此无法三等分
  度角，从而证明了尺规作图无法三等分任意角。

令

，其中

。

那么

，且

所以

是多项式

的根，这个多项式在

上不可约因为它没有整数根。所以它是

在

上的既约多项式。所以

在

上的次数是

，

也是。

[推论] 令

是素整数，如果正

-边形可以用尺规作图构造，那么对某个整数

有

。

[定理---可构造数的域] 令

都是实数域

的子域，且有性质

。那么

的每个元素都是可构造的。

[引理]

1. 可构造的数形成
   的子域。
2. 如果
   是正可构造数，那么
   也是。

证明：
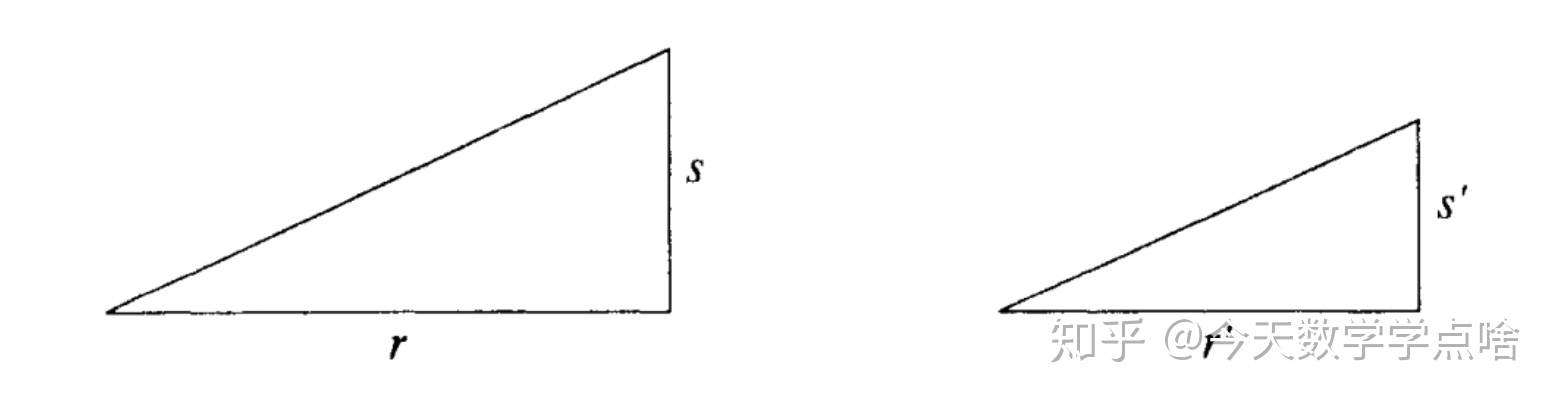
(1) 需要证明如果

是正可构造数，那么

也是可构造的。加减可以通过标注长度做到；乘除使用相似三角形：如下图，通过画平行线作相似三角形，令

，那么

；令

，那么

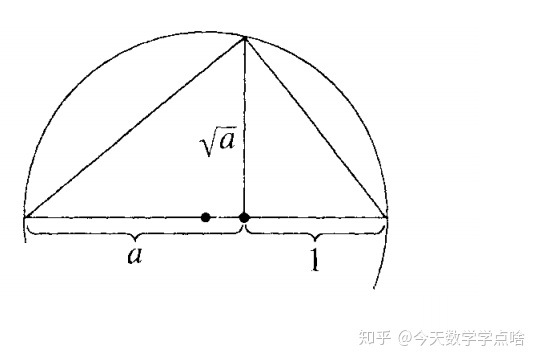
(2) 还是用相似三角形，需要作

，使得

：使用圆内接三角形，作直径为

的圆，然后作以直径为斜边的直角三角形。

---

6 添加根

[添加根到域] 给定系数属于

的多项式

，可以把

的根添加到

：构造多项式环

的商环K=F[x]/(f)，

• 构造给出同态
  ，
  的剩余
  满足关系

[引理---添加根] 令

是域，

是

中的既约多项式，那么环

是

的扩域，且

的剩余

是

在

中的一个根。

证明：因为

是极大理想，且同态

将

的元素映为常数多项式的剩余，是一个单射，所以环

是域，。所以

的像是

的一个子域，那么

是

的扩域。

• 多项式
  在
  上完全分裂，如果它在
  上的因子都是线性因子。

[命题---存在使

分裂的扩域]

令

是域，

是

上的正次数首一多项式。存在

的扩域

使得

在

上完全分裂。

证明：按

的次数归纳。初始情况：

在

上的根是

，所以

，

是某个多项式。如果假设正确，将

替换成

，完成归纳。否则，选择

的不可约因子

，存在

的域扩

，在其中

有根

，那么

也是

的一个因子。用

替换

，得到初始情况。

[命题---多项式环之间的关联] 令

使系数属于

的多项式，

，且令

使

的扩域，

1. 多项式环
   作为子环包含于
   中，所以在
   中做的运算在
   中也有效。
2. 用
   带余除
   ，在
   中和在
   中得到的结果相等。
3. 在
   中
   整除
   ，当且仅当
   在
   中整除
   .
4. 在
   中和
   中，计算得到的
   和
   的（首一）最大公因子相等。
5. 如果
   在
   中有相同的根，那么它们在
   中不是互质的。如果
   和
   在
   中不是互质的，那么存在扩域使得它们在其中有相同的根。
6. 如果
   使
   得既约元，且
   在
   中有相同的根，那么在
   中
   整除
   。

[多项式的导数] 多项式

的导数

，如果

的系数属于域

，那么它的导数

也是。

[引理---根是重根的条件] 令

是系数属于

的多项式。一个属于

的扩域

的元素

是一个重根，即

整除

，当且仅当它既是

的根，也是

的根。

证明：如果

是

的根，那么

整除

，

，那么

是

的重根，当且仅当它是

的根，

，代入

，

当且仅当

。

[命题---存在有重根的扩域的条件] 令

是系数属于

的多项式，存在

的扩域

，

在其中有重根，当且仅当

和

不是互素的。

证明：如果

在

中有重根，那么

和

在

中有相同的根，所以它们在

和

中都不是互素的。相反，如果

不互素，那么它们在某扩域

上有相同的根，从而

在其上有重根。

[命题---没有重根的条件] 令

在

中是既约多项式，

1. 在
   的任意扩域上都没有重根，除非导数
   是零多项式。
2. 如果
   是特征为
   的域，那么
   在
   的任何扩域上都没有重根。

证明：(1) 需要证明

是互素的，除非

'是零多项式。因为

是既约的，如果

不是零，那么它的次数小于

的次数，所以

和

没有公因子。

(2) 在特征为零的域上，非常数多项式的导数不是零。

• 当
  的特征
  是素数时，非常数多项式
  的导数可能是零：当所有
  的单项式的幂次都可以被
  整除时。

---

7 有限域

[有限域的阶] 有限域

的特征不是零，所以是一个素数，因此

包含一个素域

令

是次数

，作为

-向量空间，

与列向量空间

同构，

的元素数量为

，即有限域的阶是一个素数的幂，记为

:

[定理---关于有限域] 令

是素整数，

是

的正次幂，

1. 令
   是阶为
   的域。
   的元素是多项式
   的根。
2. 多项式
   在素域
   中的既约因子，是
   中的次数整除
   的既约多项式。
3. 令
   是阶为
   的域，
   中非零元组成的乘法群
   是一个阶为
   的循环群。
4. 存在阶为
   的域，且所有阶为
   的域都是同构的。
5. 阶为
   的域包含阶为
   的子域，当且仅当
   整除
   。

[推论] 对每个正整数

，在素域

上存在次数为

的既约多项式.

---

8 本原元

[本原元] 令

是域

的扩域，元素

生成

，即

，那么

称为这个扩张的本原元。

[定理---本原元定理] 特征为零的域

，

的每个有限扩域

都包含本原元。

证明：因为扩域

是有限的，

由有限的集合生成。比如

. 用

归纳，当

定理成立，所以我们假设

由单个元素

生成，那么

可由两个元素

和

生成。从而定理的证明就缩减到了

由两个元素生成的情况，需要以下引理：

[引理] 令

是特征为零的域，

是由元素

生成的

上的扩域。 除了有限多个

之外的所有

，

是

在

上的一个本原元。

证明：令

是

各自的

上的既约多项式。令

是

的扩域，在其中

都完全分裂。它们的根分别为

, 和

，其中

,

因为特征零，所以根都是互不相同的。令

当

,

仅对至多一个

成立。所以对于除了有限多个

的所有

，

都是互不相同的。需证明除了那个“坏”的

值，

是本原元。写成

令

。多项式

的根也是

。这个多项式的系数不属于

，但是因为

，

,

，所以

的系数在

中。

考察

的最大公因子

，因为

.

是那些也是

的因子的

的积，即那些

既是

的根，也是

的根。其中一个公共根是

。

当

不是

的根，所以

是唯一的

的公共根，所以

。 因为

是

的元素，所以

也是

的元素，所以

也属于

，所以

。

---

9 函数域

[函数域] 关于变量

的有理函数域

记为

，它的元素是复多项式的分式

。函数域是

的有限扩域。

[本原多项式] 令

是

的扩域

的次数为

的本原元，令

是

在

上的既约多项式，所以

同构于域

，

对应

的剩余。去分母，

变成本原多项式：

系数

是关于

的多项式，最大公因子是

，

是首一的。

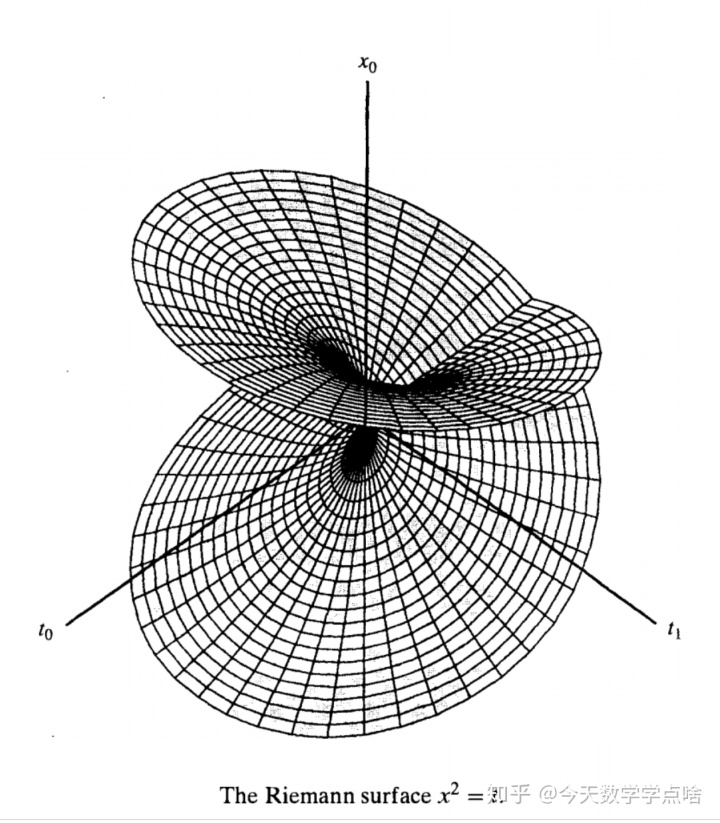
• 的黎曼面：复
  -空间
  上的轨迹
  ，
  是
  -平面
  的
  页分支覆盖。分支点是
  上的点
  ，使得单变量多项式
  有少于
  个根，即有重根或
  是
  的首项系数
  的一个根。用
  表示
  去掉一些未指定的有限子集后剩下的部分。

[扩域的同构] 域

的扩域

，

之间的同构，是同构

，它在

上被限制为恒等映射。

[分支覆盖的同构]

的分支覆盖

，

的同构是连续的，双射

与这些面到

的投影相容，

• ：从
  中删除一些有限的集合，使得
  是双射。
• 路连通：称分支覆盖
  是路连通的，如果
  是路连通的，即对
  的每个有限子集
  ，集合
  是路连通的。

[定理---黎曼存在定理]

上

次函数域的同构类，和

的连通

页分支覆盖的同构类，之间存在双射对应，使得由既约多项式

确定的扩域

的类，对应于它的黎曼面

的类。

[命题---同构扩域对应同构覆盖] 令

和

分别是

和

中的既约多项式。令

和

是由它们定义的扩域，且令

是黎曼面

。如果

和

是同构的扩域，那么

是同构的

的分支覆盖。

证明：

在

中的剩余称为

，是

的一个根，即

，且一个

-同构

给出了

在

中的一个根：

，所以

可以表示为

中一个元素模

的剩余，令

是这个元素，定义同构

为

因为在

中

，而在

中

表示

，所以

属于理想

，存在

使得

如果

是

中的点，那么

，且

。所以

是

中的点。

因为

，所以它们的系数是关于

的有理函数，可能有分母，所以

在一个有限的点集上没有定义。

的逆函数通过交换

，

得到。

[剪切和粘贴] 以

的黎曼面

为例，如上图，

• 剪切：沿
  的负半轴剪开，将
  分成了
  。
• 粘贴：用以下方式构建和
  同构的分支覆盖。
  和
  是复平面
  的两个副本，将它们叠起来沿实轴负半轴剪开，这些
  的复制称为页。然后将
  的
  边与
  的
  边粘贴，
  的
  边与
  的
  边粘贴。

[剪切n页分支覆盖] 给定

页分支覆盖

，令

是

上的分支点的集合。

• 对
  ，选择不相交的从
  到无限的半直线
  ，沿着这些半直线剪开
  ，也在所有位于半直线上方的点处剪开
  。
• 剪开
  意味着去掉所有
  中的点，包括
  ；剪开
  意味着去掉所有这些位于半直线上方的点。

[引理---X会被剪成ｎ页] 当

在

上方被剪开时，它分解成了

个页

的并，可以任意标号排序。每个页双射地投影到平面

。

[粘贴n页分支覆盖] 平面

的

个副本称为页，标记为

，堆叠在

上方。在

上，绕分支点

逆时针转一个圈

，称没越过

的那一边为

边，越过

的那一边

边。记页

的两边为

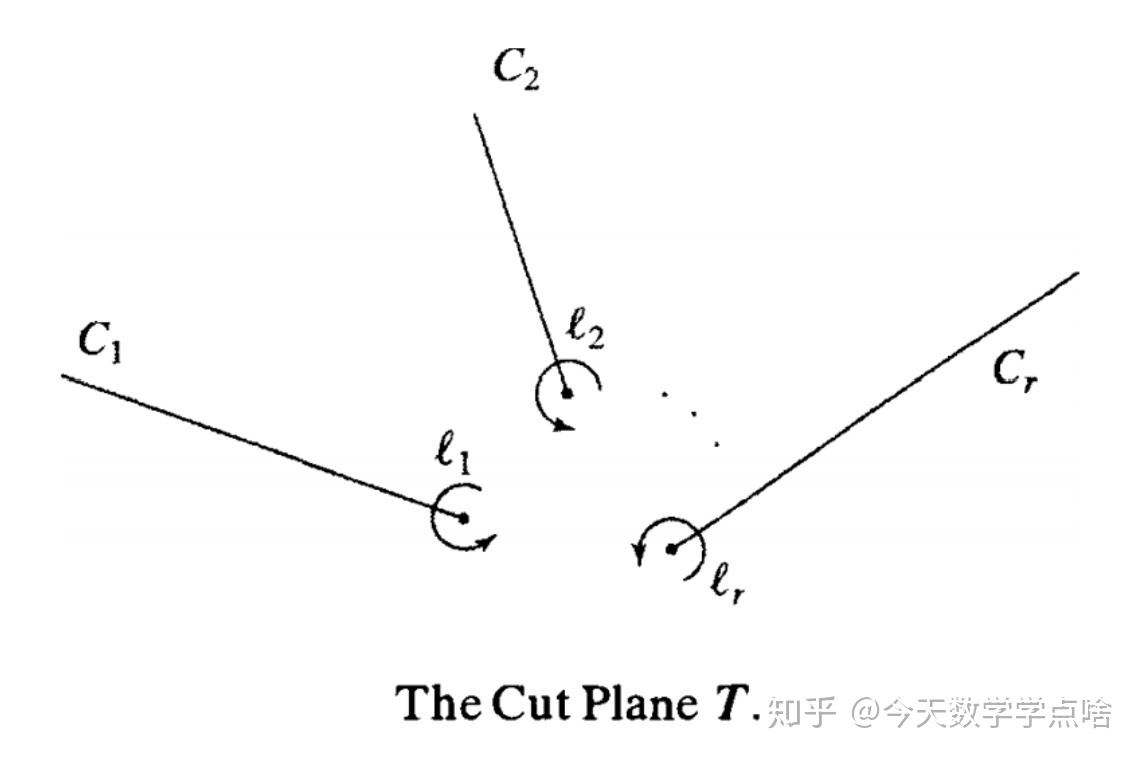
• 分支数据：对于
  ，给定指标
  的置换
  。
• 粘贴规则：如果
  ，那么沿
  将边
  和
  粘合。
• 真分支点：如果
  是平凡置换，那么每个页和自己粘合，就不需要剪切，所以称
  不是真的分支点。

[引理---每个分支覆盖都可通过剪切粘贴构造] 每个

页分支覆盖

都同构于一个用剪切粘贴步骤构造出的

页分支覆盖。

• 页的标号是任意的。
• 置换
  由分支覆盖
  唯一确定。一个标号置换
  会把
  变成共轭

[引理---分支覆盖同构的条件] 令

是通过剪切粘贴，用相同的点

和半直线

构造出的分支覆盖。设

和

是定义粘贴数据的置换。那么

是同构的分支覆盖，当且仅当存在置换

使得对每个

有

。

[引理---分支覆盖路连通的条件] 通过剪切粘贴构造的分支覆盖

，是路连通的，当且仅当置换

生成对称群的子群

，且

可迁地作用在标号

上。

证明：每个页是路连通的。如果置换

将

映为

，那么页

就会沿

粘贴到一起，那么从

的一点到S_j的一点之间就会存在跨越切口的短路。又因为页是路连通的，所有

的点可以用路连通，所以

是路连通的，当且仅当对每一对

，都存在置换

的序列使得

而这成立当且仅当

的作用可迁。

[计算置换] 将黎曼曲面与我们熟知的黎曼曲面关联起来，即

的黎曼曲面

。令

是

的分支点，其中

是形如

的多项式。

替换

, 得到单变量多项式

[引理---置换包含k循环的条件] 令

是

的根，假设：

• 是
  的
  -重根，且
• 偏导数
  在点
  处非零。

那么在点

处，页的置换包含一个

-循环。

---

10 代数基本定理

[代数封闭] 域

是代数封闭的，如果每个正次数系数属于

的多项式在

中都有根。

[代数基本定理] 每个复系数非常数多项式都有一个复根。

证明大纲：要证复系数非常数多项式

有一个复根。如果

，那么

是一个根，所以假设

定义了从复

-平面到复

-平面的函数，令

是圆点在

-平面的半径为

的圆，写成参数形式

，我们考察

的像

例子：如果

，那么当

从

取到

，点

绕半径为

的圆一次，同时，

从

到

，点

绕半径为

的圆

次。

令

是第一行的多项式，对于足够大的

，

是

的主要项，令

是

的最大绝对值，那么如果

由这个不等式，当

从

取到

，

绕半径为

的圆转

圈，

也绕原点转了

圈。

改变半径

，因为

是连续函数，像

会随着

连续地变化。当

很小时，

绕常数项

附近形成一个小圈，这个小圈不包围原点。但是当

足够大时

会绕原点转

圈，唯一的解释就是对于某些中间半径

,

经过了原点，这意味着对于圆

上的某个点

，

，即

是

的一个根。

---

下一章：

今天数学学点啥：代数Artin(十六): 伽罗瓦理论（完结）​zhuanlan.zhihu.com