gcn 图卷积神经网络_图卷积神经网络(Graph Convolutional Network, GCN)

从谱聚类说起

谱聚类(spectral clustering)是一种针对图结构的聚类方法，它跟其他聚类算法的区别在于，他将每个点都看作是一个图结构上的点，所以，判断两个点是否属于同一类的依据就是，两个点在图结构上是否有边相连，可以是直接相连也可以是间接相连。举个例子，一个紧凑的子图（如完全图）一定比一个松散的子图更容易聚成一类。

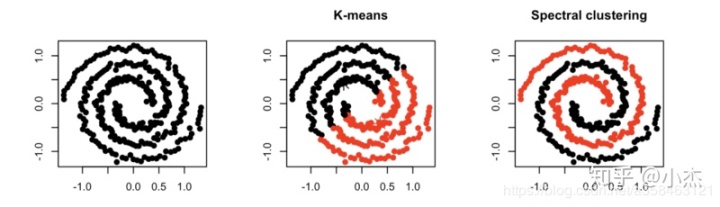
那谱聚类为什么叫谱而不是图聚类呢？这个spectral是什么东西？我们知道一个图是可以用一个邻接矩阵A来表示的。而矩阵的谱（spectral）就是指矩阵的特征值，那么这个特征值跟图的矩阵到底有什么深刻的联系呢？
那么首先，图的聚类是什么？我们可以将聚类问题简化为一个分割问题，如果图的结点被分割成A,B这两个集合，那么我们自然是希望在集合中的结点的相互连接更加紧密比如团，而使得子图之间更加尽可能松散。
为了建立这个联系，我们介绍一个laplace matrix：

D是一个对角矩阵，每个对角元素

表示第i个结点的度。A则是这个图邻接矩阵。为什么要这样去构造一个矩阵呢？因为研究图的一些性质的时候，我们常常用到一个类似于下式的目标函数：

这里E表示只有u，v之间有边才会执行求和操作。这个目标函数可以定义图上的很多问题，比如最小图分割问题，就是要找到一个方法将图分成两块的使得切割的边最少（如果边有权重那就是切割的权重最小）。如下图，你不能找到一个比切两条边更少的分割方法了。

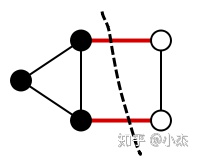
而这个优化问题其实等价于当

的时候:

而这个方程不正是一个二次型吗。为了让二次型得到这个结果。我们发现，当

的时候就可以了。验证一下：

此外，当A不是邻接矩阵而是权重矩阵W的时候，于是d就从度推广到权重的求和，那么这个公式还可以推广为：

RatioCut 切图聚类

现在，我们可以尝试将这个目标函数与Ratio切图聚类的目标函数建立起联系，建立联系有什么好处呢？好处就是如果我们发现切图的目标函数是这个二次型，那么我们只要优化这个二次型，不就可以用连续的方法来解决一个离散的问题吗？
RatioCut考虑最小化

，同时最大化每个子图的个数即：

其中

表示两个子图之间的距离(两个子图结点之间距离的求和)：

这里公式里的是A与A的补集的切图权重（切的边权重的求和），也就是说我们希望子图A与其余的图分离的代价最小，比如我只要切掉一条微不足道的边就能将两个复杂的图（比如两个团）分离开，那么就可以认为这是一个好的切割。

现在我们仿照上面的x，将其推广到多个簇，于是我们用一个指示函数（one-hot）来表达每个结点属于哪个子图，这样就将切割问题跟二次型建立起了联系

我们引入指示向量

，表示有k个子图，对于任意一个向量

, 它是一个|V|-维向量（|V|为结点数，用来标记哪个结点属于哪个子图，类似于one-hot），我们定义

为：

那么，对于每一个子图都有：

其原理在于，因为当

时，因为结点

属于子图i，结点

不属于子图i，于是

，同理，当

,

都属于子图的时候

。

上述是第i个子图的式子，我们将k个子图的h合并成一个H，于是式子变成：

也就是说Ratiocut本质上就是在最小化

这个东西。那么怎么优化呢？注意到每个

都是相互正交的，因为一个结点不能同时属于多个类别，因此H是一个正交矩阵，又因为L是一个对称矩阵，那么可以证明，H是L的特征向量的时候，恰好是这个优化问题的解，我们需要要找到那么特征值比较小的特征向量，就可以找到一种代价最小的切割方法。我们可以来证明一下,特征向量恰好是他的极值：

这里用到了一些最优化求导常用公式技巧，其实这个推导跟PCA是一样的，只不过PCA找的是最大特征值（PCA中L是协方差矩阵，目标是找到一个向量最大化方差），这里是找最小特征值，我们目标是找到一个向量最小化这个二次型矩阵。

(PS: 想知道为什么是找特征值最小，而PCA找的是特征值最大的同学，不妨看看我的另外一篇文章：

小杰：谱图理论(spectral graph theory)​zhuanlan.zhihu.com

最后，通过找到L的最小的k个特征值，可以得到对应的k个特征向量，这k个特征向量组成一个n*k维度的矩阵，即为我们的H。一般需要对H矩阵按行做标准化，即

由于我们在使用维度规约的时候损失了少量信息，导致得到的优化后的指示向量h对应的H不能完全指示各样本的归属（因为是连续的优化，不可能恰到得到一个one-hot向量），因此一般在得到nxk维度的矩阵H后还需要对每一行进行一次传统的聚类，比如使用K-Means聚类，从而得到一个真正的one-hot指示向量。

所以谱聚类的流程可以总结如下：

1. 计算标准化后的lapace矩阵

2. 求解标准化lapace矩阵的特征值与特征向量

3. 取最小的k1个特征值,及其对应的特征向量f

4. 将f排列成一个n*k1的矩阵，对矩阵的每一行进行标准化，然后使用k means聚类，聚类数为k2

5. 得到k2个簇，就是对应k2个划分。

GCN

图卷积神经网络，顾名思义就是在图上使用卷积运算，然而图上的卷积运算是什么东西？为了解决这个问题题，我们可以利用图上的傅里叶变换，再使用卷积定理，这样就可以通过两个傅里叶变换的乘积来表示这个卷积的操作。那么为了介绍图上的傅里叶变换，我接来下从最原始的傅里叶级数开始讲起。

从傅里叶级数到傅里叶变换

此部分主要参考了马同学的两篇文章：

1. 从傅立叶级数到傅立叶变换
2. 如何理解傅立叶级数公式？

傅里叶级数的直观意义

如下图，傅里叶级数其实就是用一组sin，cos的函数来逼近一个周期函数，那么每个sin，cos函数就是一组基，这组基上的系数就是频域，你会发现随着频域越来越多（基越来越多），函数的拟合就越准确。

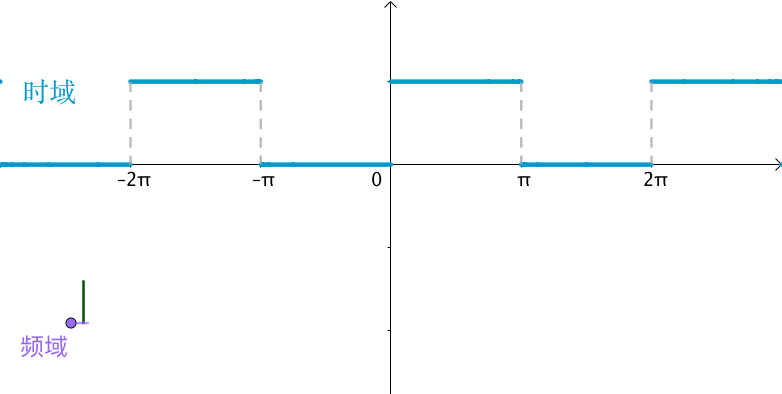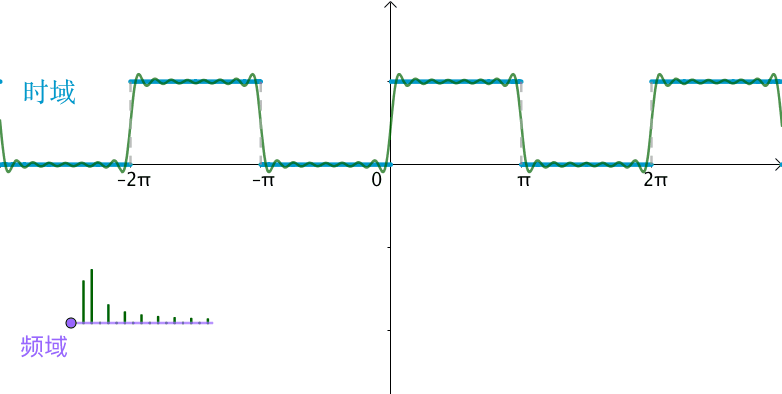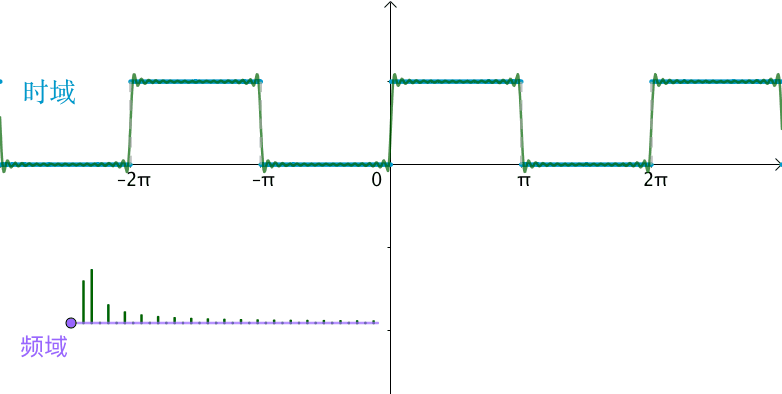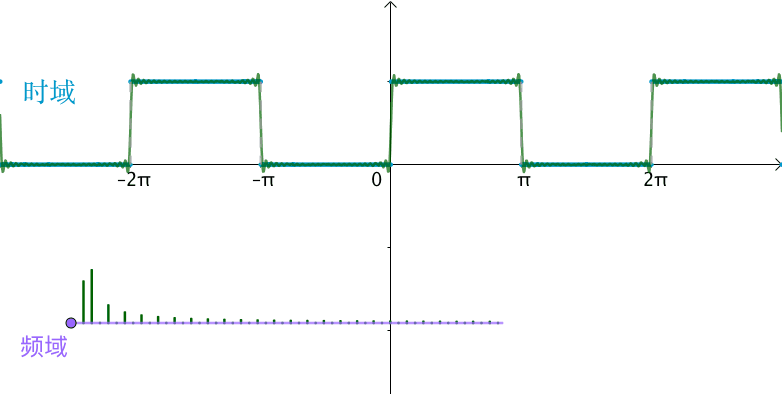
傅里叶变换推导

要讲傅里叶变换的推导，我们要先从傅里叶级数讲起，考虑一周期等于T，现定义于区间[-T/2,T/2]的周期函数f(x)，傅里叶级数近似的表达式如下:

利用偶函数*奇函数=奇函数的性质可以计算出

与

利用欧拉公式

x，我们发现

可表示成

再将傅立叶级数f(x)中

和

的线性组合式改写如下：

可以验证

，这是因为an是一个偶函数，bn是一个奇函数。此外，若n=0，就有

。将以上结果代回f(x)的傅立叶级数即得指数傅立叶级数：

现在我们知道

，将

的结果代进去可以得到：

公式用频率替换：

，再令

现在我们可以写出全新的傅里叶级数：

现在令

，并设

于是得到了傅里叶变换就是

Signal Processing on Graph

在将图的傅里叶变换之前，我们先介绍一下图信号是什么。我们在传统概率图中，考虑每个图上的结点都是一个feature，对应数据的每一列，但是图信号不一样，这里每个结点不是随机变量，相反它是一个object。也就是说，他描绘概率图下每个样本之间的图联系，可以理解为刻画了不满足iid假设的一般情形。

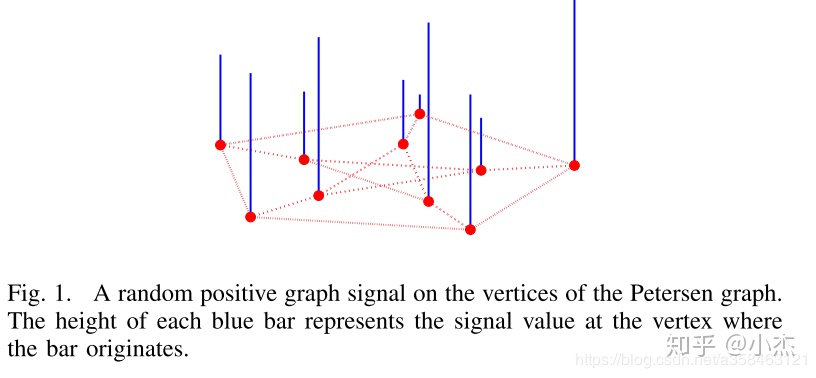
图上的傅里叶变换

那么我们要怎么将传统的傅里叶变换推广到图结构中去？回忆一下，传统对f作傅里叶变换的方法：

我们换了种写法，其实我们发现这个傅里叶变换本质上是一个内积。这个

其实是lapace算子的一个特征函数，可以理解为一种特殊形式的特征向量：

注意，这里导数本质上是一个线性变换，因为它满足线性算子的两个性质，T(x+y)=T(x)+T(y), cT(x)=T(cx)。可以看到

是laplace算子的特征向量，而

则是lapace算子的特征值。那么在图上我们的laplace矩阵就是离散化的lapace算子，而这个算子在图上的基显然就是特征向量了！

关于拉普拉斯算子的直观理解推荐看这篇文章：

如何理解 Graph Convolutional Network（GCN）？​www.zhihu.com

因此，只要意识到传统的傅里叶变换本质上求的是与正交基的内积（比如基

）上的系数，而推广到图上的正交基很显然就是laplace矩阵的特征向量，于是对于图向量的傅里叶变换就可以表达为:

是Graph上的

维向量，

与Graph的顶点一一对应，

表示第

个特征向量的第

个分量。那么特征值（频率）

下的，

的Graph 傅里叶变换就是与

对应的特征向量

进行内积运算。

这个变换就是在求解特征向量的系数，类似于基的系数“频域”。为什么呢？首先f是图上的某个向量，于是我们可以用正交基将其展开：

那么f跟

的内积就是：

因为

跟其他特征向量都正交，所以内积等于0，而跟自己的内积则等于1，所以结果就等

.

因此，可以理解为图上的经过傅里叶变换后的函数

就是一个计算特征向量的系数的函数。

更一般的，图上的傅里叶变换可以写成以下内积的形式，其中U是laplace矩阵的特征向量矩阵：
傅里叶变换：

傅里叶逆变换：

因此，我们就可以定义图上的卷积，因为它就是简单的两个变换的乘积然后再逆变换而已：
比如，x,y的卷积，就是他们傅里叶变换频域对应相乘，再通过傅里叶逆变换求回去

又因为

因此我们将

参数并化为一个对角矩阵，设

，从而可以训练一个卷积核：

然而计算U的代价太高了，因此要想办法去近似它，有人提出，

其中

，现在假设

,并且k=1，于是

最后再假设这两个参数是共享的，可以得到：

最后，再将中间的项用一个trick变成：

，其中

,

，最后的最后，终于得到了这样的近似卷积公式：

这样我们就可以直接用神经网络训练了：

参考资料

https://towardsdatascience.com/spectral-clustering-82d3cff3d3b7

https://www.cnblogs.com/pinard/p/6221564.html

https://tkipf.github.io/graph-convolutional-networks/

https://ccjou.wordpress.com/2012/04/03/%E5%82%85%E7%AB%8B%E8%91%89%E7%B4%9A%E6%95%B8-%E4%B8%8B/

https://www.matongxue.com/madocs/712/

https://www.youtube.com/watch?v=Q99ZPGnUBAQ

https://www.bilibili.com/video/av39809391?from=search&seid=14221165253248461631