泊松分布中入可以为0吗_ZIPtoo many Zero：零膨胀泊松回归模型

? 连享会主页：lianxh.cn

New！ lianxh 命令发布了：   GIF 动图介绍
随时搜索 Stata 推文、教程、手册、论坛，安装命令如下：. ssc install lianxh

  连享会 · 最受欢迎的课

 
? 2021 Stata 寒假班
⌚ 2021 年 1.25-2.4

? 主讲：连玉君 (中山大学)；江艇 (中国人民大学)

? 课程主页：https://gitee.com/arlionn/PX

作者：郑浩文(中山大学)邮箱：zhenghw25@mail2.sysu.edu.cn

---

目录

• 1. 计数模型与 ZIP

  • 1.1 计数模型的使用

  • 1.2 零膨胀问题与 ZIP

  • 1.3 模拟零膨胀数据

• 2. Stata 实操文章

  • 2.1 翻译说明

  • 2.2 正文

  • 2.3 译注及扩展

• 3. 参考文献

• 4. 相关推文

---

1. 计数模型与 ZIP

1.1 计数模型的使用

现实中，存在一类模型，其解释变量是离散的，如事件发生次数、物品个数等，这类模型被称为计数模型。

计数模型一般使用现有分布来拟合解释变量的频率，根据数据特征可使用正态分布、泊松分布、负二项分布等。而因为解释变量非连续，且当解释变量取值有明确上下界(如非负约束)时，正态分布通常不适用，而泊松分布等将有更好的拟合效果。计数模型的估计往往使用极大似然估计。

考虑以泊松分布来建模。根据泊松分布，随机变量取值为 ( 为非负整数)时， 概率为：

为保证 非负，令 。则代入上述概率公式后我们将得到泊松回归模型。

以下 Stata 代码可以生成一个满足泊松分布的变量 poi。

. set obs 100000 // 设置 100000 的样本量
. set seed 1234  // 设置种子值

. gen poi = rpoisson(4) // λ 为 4 的泊松分布随机
. hist poi ,fraction xtitle("yi") ytitle("Pr") // 绘制直方图

分布如图：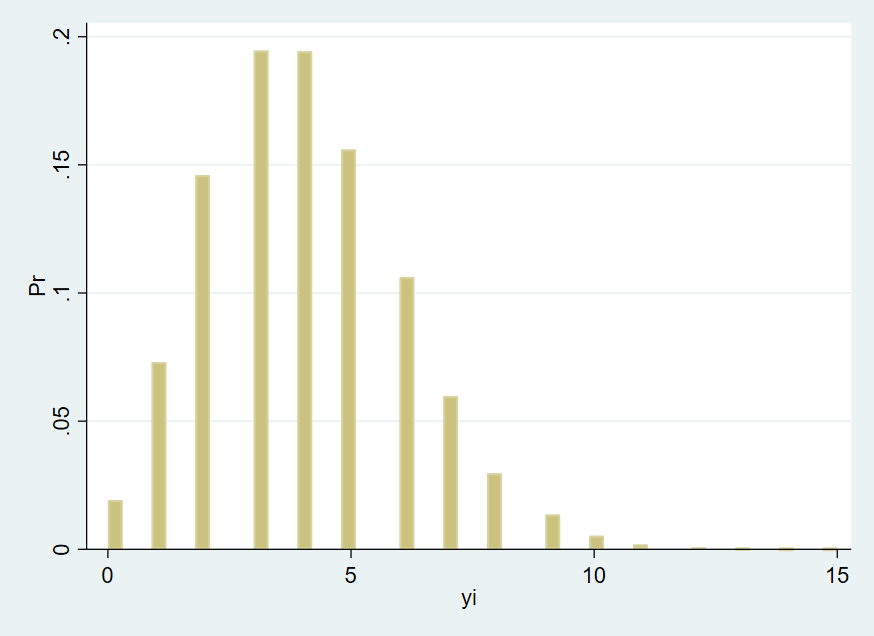

1.2 零膨胀问题与 ZIP

观察上图可以发现，取值的概率随着取值的增大而先增大后减小。然而，在一些场景下，0 取值的频率很高，无法使用普通泊松分布解释，于是出现了所谓零膨胀问题。如在车险理赔次数的频率拟合中，存在许多的零赔付的保单。这可能由两部分原因组成：一是车祸发生的概率较低，二是车主对一些影响较小的擦碰选择不索赔，以免续保时保费增加。

为此，需要对泊松回归模型进行一定的修正。以车险为例，假设实际发生事故并可理赔的次数满足泊松分布，而车主在发生事故后有 的概率不索赔，则修正后的模型为零膨胀回归模型(ZIP)，方程如下：

其中，。方程第一行两个加数中的 可以认为是超额零值的占比。

同时，方程可以等价地表示为两个相互独立随机变量乘积的分布，一个变量满足 0-1 两点分布，另一个满足泊松分布：

因此可以将 ZIP 分为两个部分：

• 第一部分使用 Logit(或 Probit ) 回归研究 ，
• 第二部分使用泊松回归研究 。

以 ZIP 的基本思想为基础，可以拓展出 满足其他分布的零膨胀模型，如负二项分布、广义泊松分布等。我们可以根据数据的均值方差特征来选择。

1.3 模拟零膨胀数据

通过以下 Stata 代码可以构造零膨胀的数据。方法是先构造基分布(两点分布和泊松分布)，再对泊松分布进行零膨胀处理。

. set obs 100000 // 设置样本量
. set seed 1234  // 设置随机数种子

. gen poi = rpoisson(4)  // 参数为 4 的泊松分布
. gen assign = runiform(0,100) // 分配变量 assign 满足 0-100 的均匀分布

. scalar separate = 12  // 设置分配变量阈值

. gen num = poi // 变量 num 满足零膨胀后的分布
. replace num = 0 if assign<=separate // 分配变量<=12的 变量设置为 0
. * 相当于两点分布随机变量取 0 值的概率为 12%

num 的直方图如下，曲线为泊松分布：

2. Stata 实操文章

温馨提示： 文中链接在微信中无法生效。请点击底部

2.1 翻译说明

翻译并修改自 ZERO-INFLATED POISSON REGRESSION | STATA DATA ANALYSIS EXAMPLES。原文使用 Stata 12，本文使用 Stata 15 重现结果，差异之处通过译注形式说明。

2.2 正文

离散的计数数据常用泊松回归模型来拟合。若数据集中包含过多的零时，数据的分布就与标准泊松分布有较大偏差，此时应该进行修正。理论表明，数据中零的产生是一个相对独立的过程，可以与其他数据分开建模。由此，零膨胀泊松回归模型( ZIP )应运而生。模型分为两个子模型：Logit模型和泊松计数模型。前者用于拟合零值的频率，后者用于拟合其他值的频率。关于这两个模型的使用，可以参考以下两篇数据分析样例介绍：泊松回归 、Logit回归 。

注：本文意在展示如何使用各种数据分析命令，并不完全覆盖研究者应有研究过程的各个方面。例如，文章不包含数据清洗和检查、假设检验、模型诊断和其他后续可能进行的分析过程。

适用的样例

例 1.学校管理者研究了两所高中的高二学生在某一个学期中的出勤表现。出勤指标的定义是缺勤天数，并使用性别、三科(数学、语文和艺术)标准化后的成绩共四个变量进行预测。大多数学生整个学期都没有缺勤记录，意味着零值的频率很高。

例 2.州野生生物学家想对一个州立公园内渔夫的捕鱼量进行建模。他们向游客收集以下信息：是否有野营车、团队中的人数、团队内是否有小孩和捕鱼数量。数据中样本捕鱼量为零原因有两种：一是游客没有去抓鱼，二是没有抓到鱼。前者是导致数据零值频率偏高的原因，而数据中并没有包含是否有去抓鱼的信息，因此无法将两者分开。

数据介绍

让我们用 ZIP 模型来探究上述的样例 2，使用的数据集为 Stata 手册附带数据 fish.dta。该数据集中一共有 250 群游客，每一群游客都被问及：捕鱼量(count)、有几个孩子(child)、总人数(persons)和是否有野营车(camper)。

在预测捕鱼量的同时，我们还可以预测超额零值的频率，即有多少零值不是因为抓不到鱼而产生的。

*. use http://www.stata-press.com/data/r10/fish, clear
. webuse "fish.dta", clear 
. summarize count child persons camper

 Variable |  Obs    Mean    Std. Dev.   Min    Max
----------+---------------------------------------
    count |  250   3.296