origin函数绘图_如何利用Origin进行多元线性回归、指数拟合和非线性曲面拟合？...

推荐阅读

免费课程30节丨从入门到高手，用Origin处理CV、XRD、XPS、FTIR、Raman、TGA、DSC数据

【免费】3节课学会24张酷炫美图 — 史上最强Origin绘图特训营！【免费】56节课56项技能，史上最强Origin教学课程史上最全！十全十美，10套10G Origin实用教程3天搞定140张Science/Nature顶刊美图，Origin技能满格！ 今天给大家介绍的是 多元线性回归、指数拟合和非线性曲面拟合。 一、多元线性回归 多元线性回归用于分析多个自变量与一个因变量之间的线性关系。下式为一般多元线性方程。 Y=A+B₁X₁+B₂X₂…+B_nX_n  Origin在进行多元线性回归时，需将工作表中一列设置为因变量(Y)，将其他的设置为自变量(X₁,X₂,X₃,…,X_n)。 实例演示： (1)导入要拟合的数据集，如图1所示。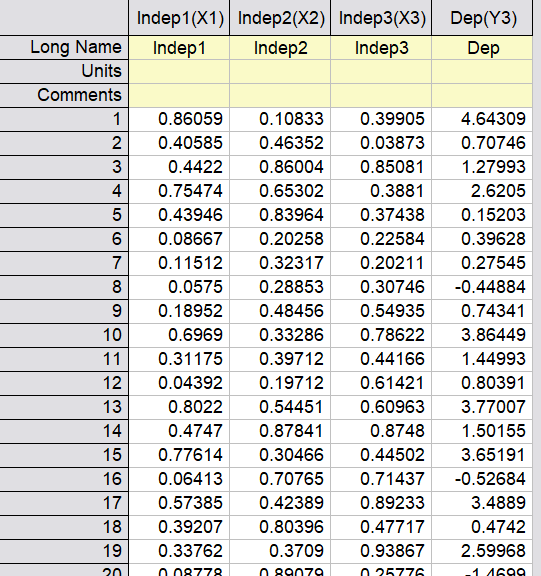 图1 原始数据 (2)选择执行菜单命令Analysis→Fiting→Multiple linear regression，进行多元线性回归，系统会弹出Multiple Regression窗口，如图2所示。 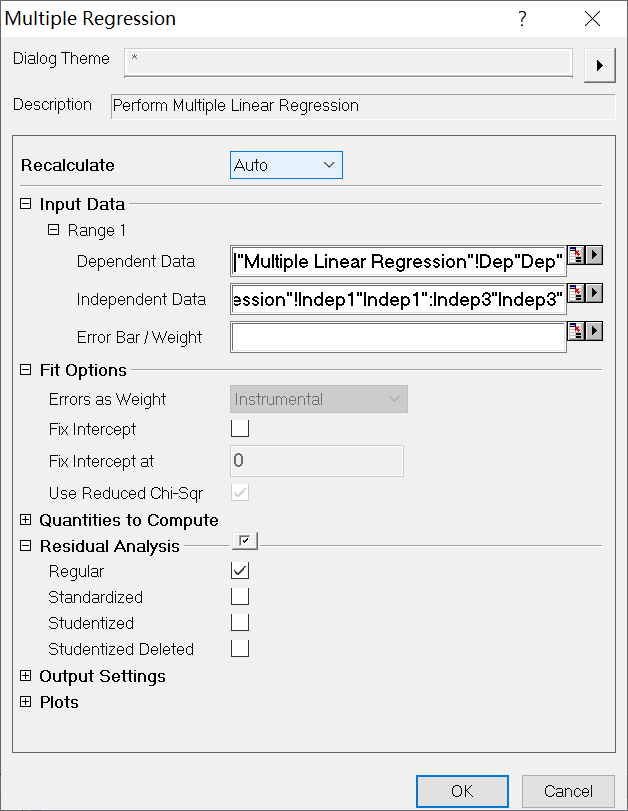图2  Multiple Regression窗口 在Multiple Regresion对话框中，设置因变量(Y)和自变量(X1，X2，X3 …)，如图3所示，单击OK按钮确定。 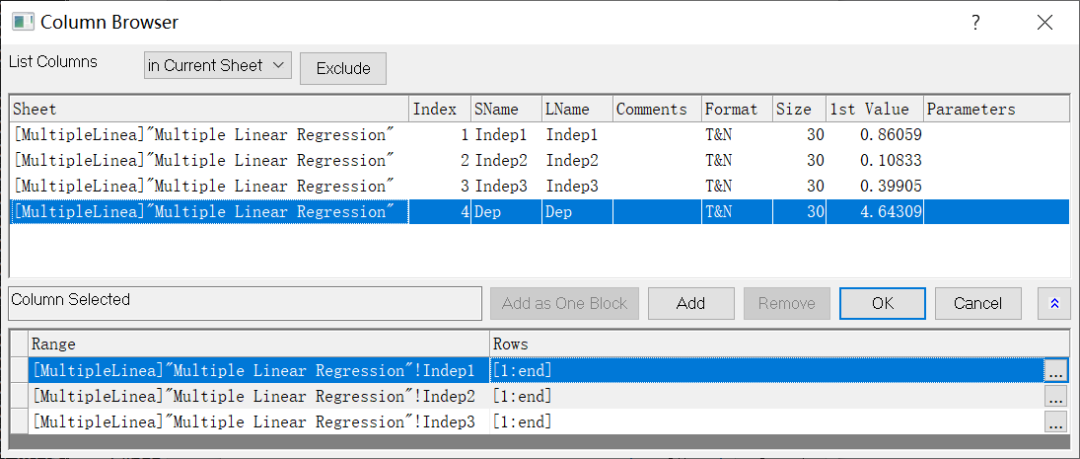图3 设置因变量和自变量 (3)根据输出设置自动生成了具有专业水准的多元线性回归分析报表，如图4所示。 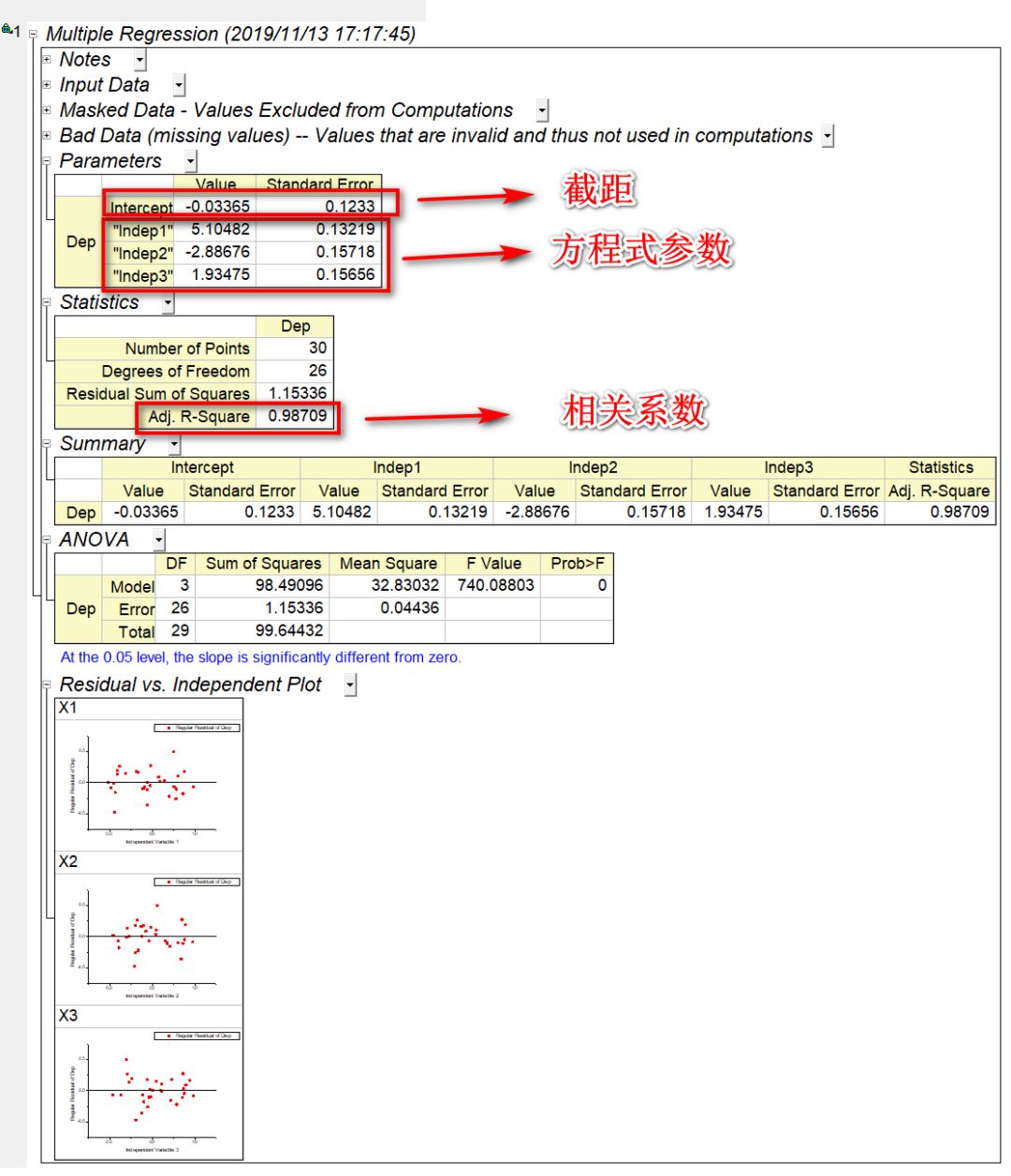图4 多元线性回归拟合报告 拟合函数：Y=-0.03356+5.10482X₁-2.88676X₂+1.93475X₃ 相关系数：0.98709 二、指数拟合 指数拟合可分为指数衰减拟合和指数增长拟合，指数函数有一阶函数和高阶函数。 实例示范： (1)导入数据，工作表如图5所示。 图5 指数拟合原始数据表 (2)选中数据中的    A(X)、B(Y)列绘制散点图。 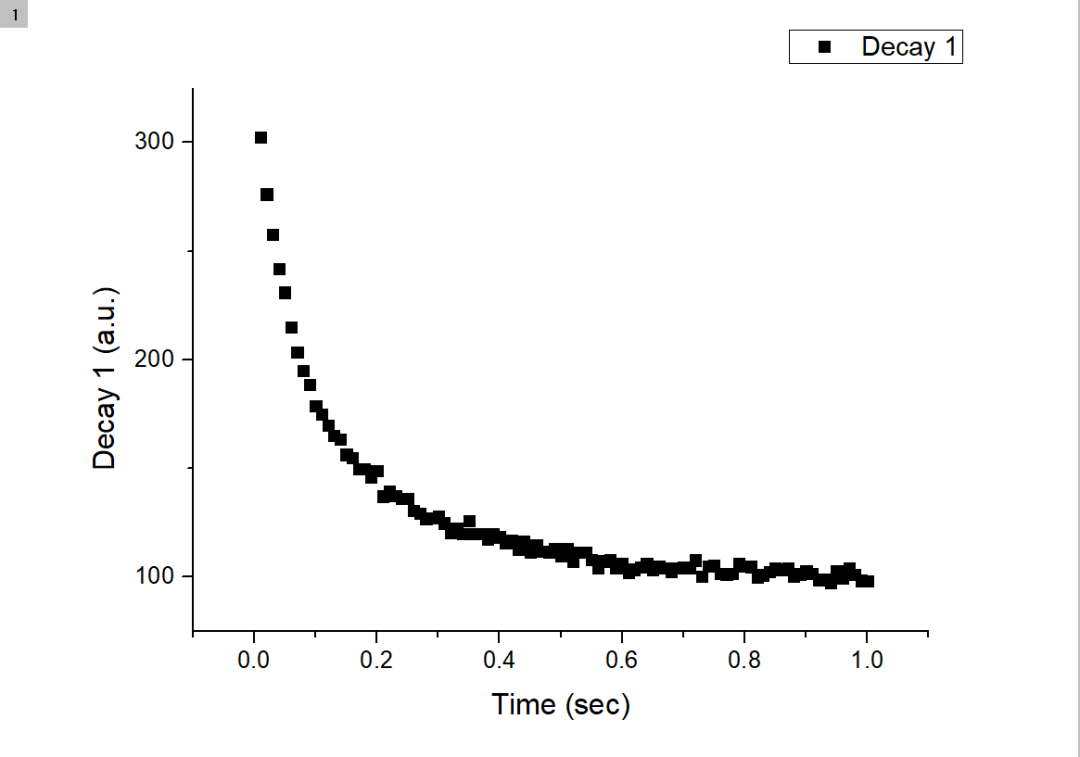选择菜单命令Analysis→Fitting→Exponential Fit，打开“NLFit”对话框。 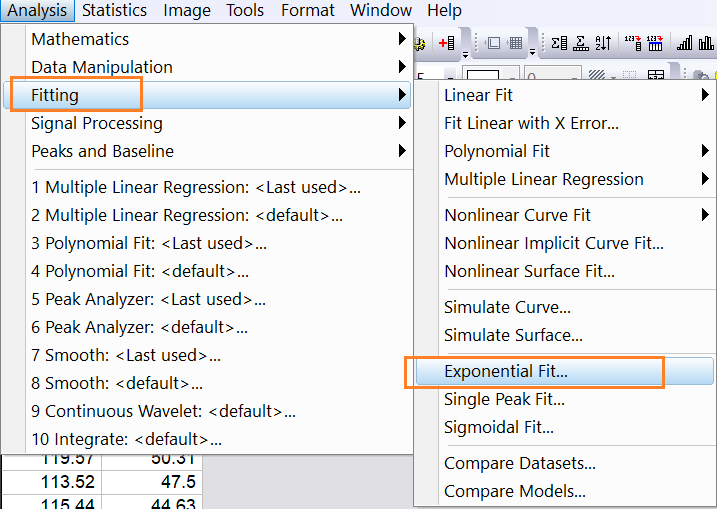此时，在“Function”下拉列表框中，给出了用一阶指数衰减函数的拟合，如图6所示。如果需要更改指数衰减函数的阶数，可以在“Function”下拉列表框中进行选择。 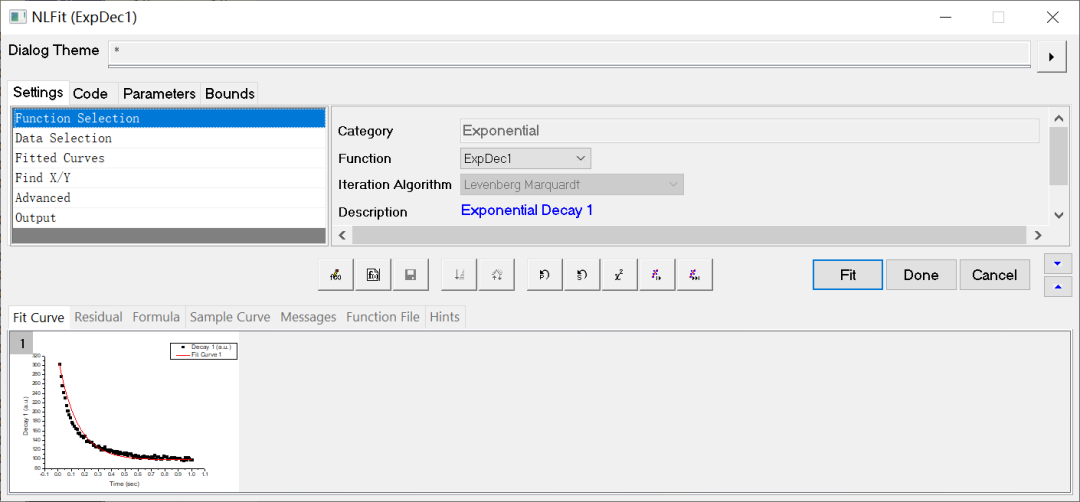图6 NLFit对话框下“Function”下拉列表 单击“NLFit”对话框的“Parameter”标签，选择对象参数性质的设置。如图7所示，将y0和A1设置为常数。 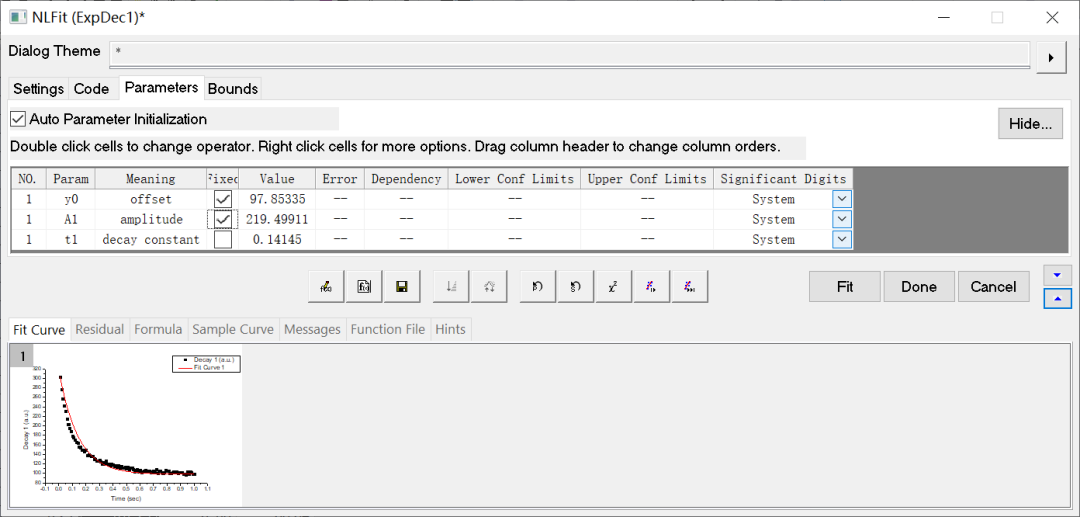图7 “NLFit”对话框的“Parameter”标签 (3)该对话框的下半部分，如图8所示。单击不同的标签可以分别看到拟合效果、拟合函数和其他信息。图8和图9分别为拟合效果图和拟合函数。 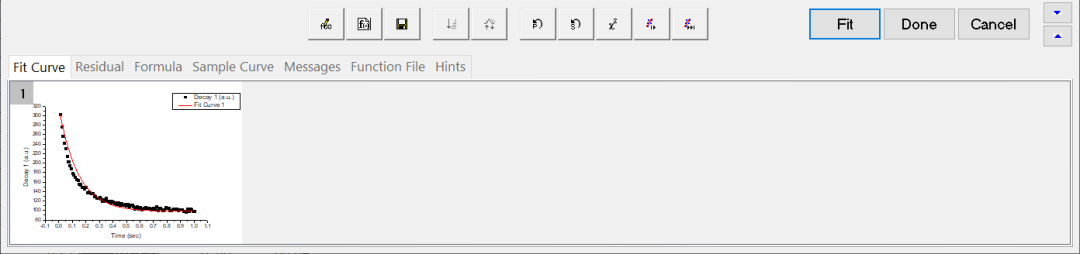图8  “NLFit”对话框下半部分效果图 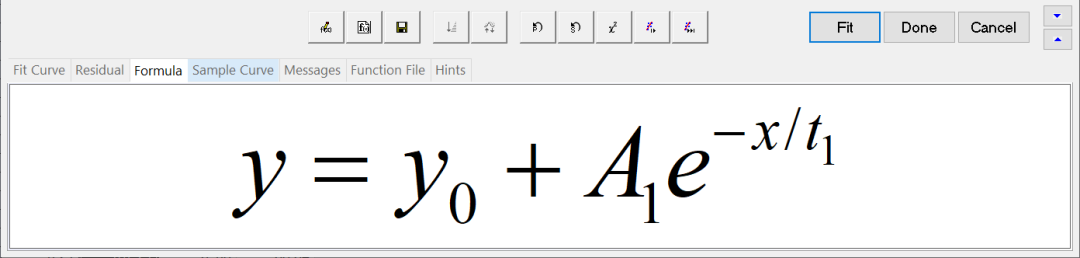图9 “NLFit”对话框下半部分“Function”下拉列表 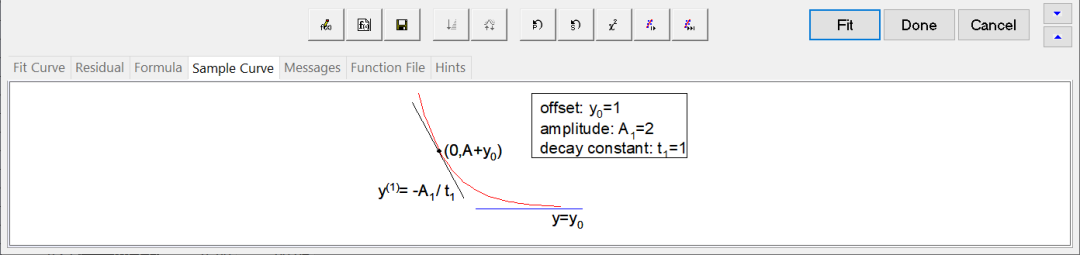图10  “NLFit”对话框下半部分“Sample Curve”下拉列表 (4)单击“Fit”按钮，完成对数据用一阶指数衰减函数的拟合，根据输出设置自动生成拟合参数分析报表和拟合数据工作表。如图11为拟合曲线所示。图12为输出分析报告表。 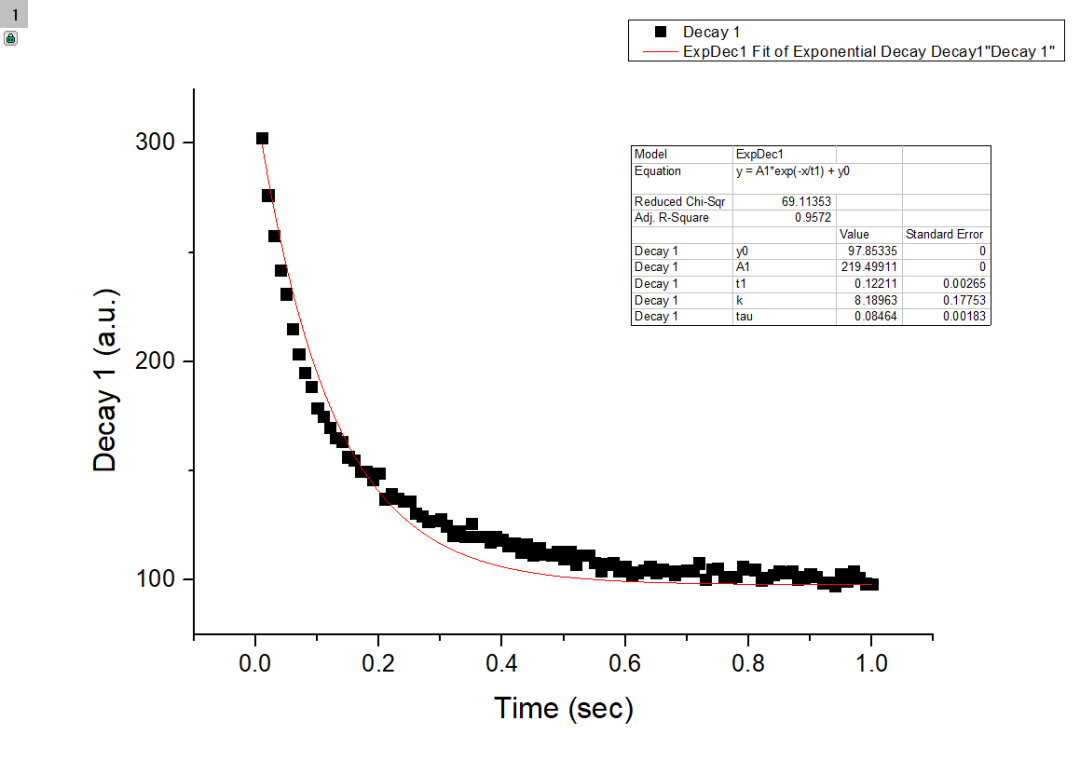图11 一阶衰减指数函数对数据拟合图形 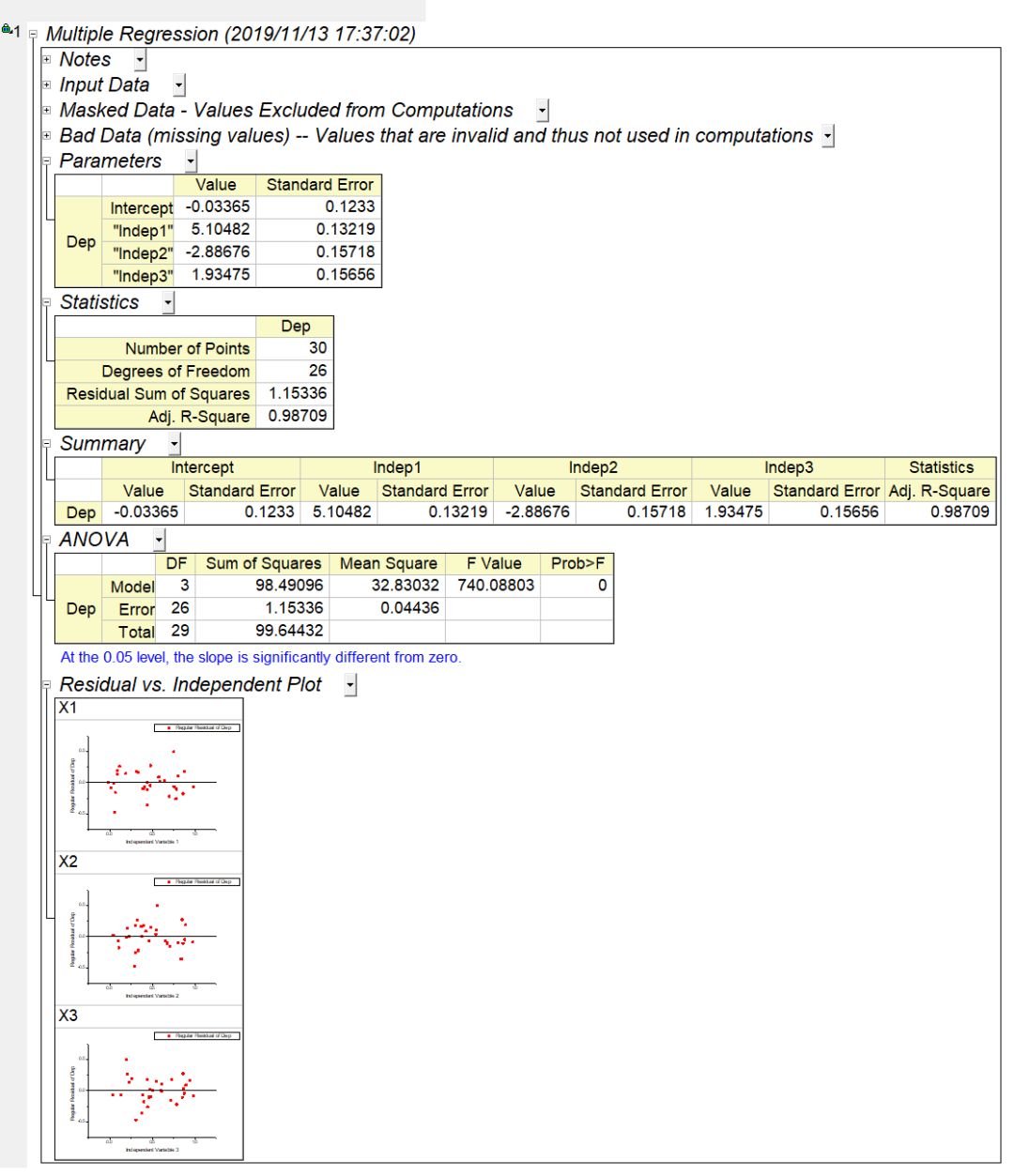图12 分析报告表 三、非线性曲面拟合 非线性曲面拟合是通过内置的表面拟合函数可以完成对三维数据的拟合。非线性曲面拟合操作与非线性曲线拟合基本相同。 如果拟合数据是工作表数据，需要工作表有XYZ列数据，选中工作表中XYZ列数据，选择菜单命令，即可完成非线性曲面拟合；如果拟合数据是矩阵工作表数据，选中矩阵工作表中数据，选择菜单命令Analysis→Nonlinear Matrix Fit，即可完成非线性曲面拟合。 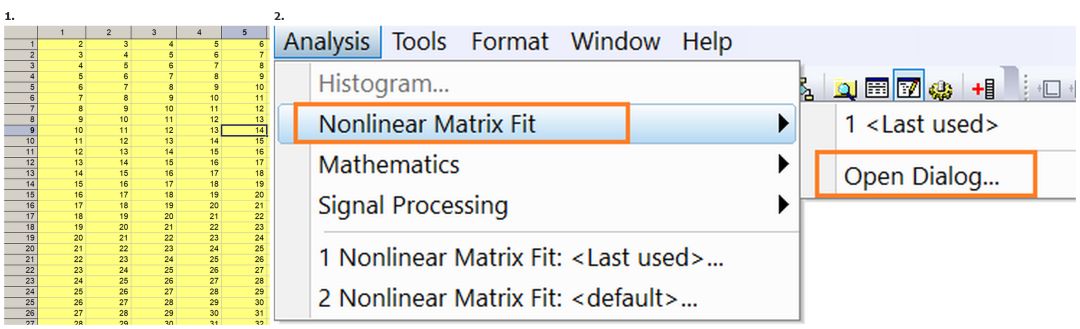图13 矩阵工作表数据非线性曲面拟合 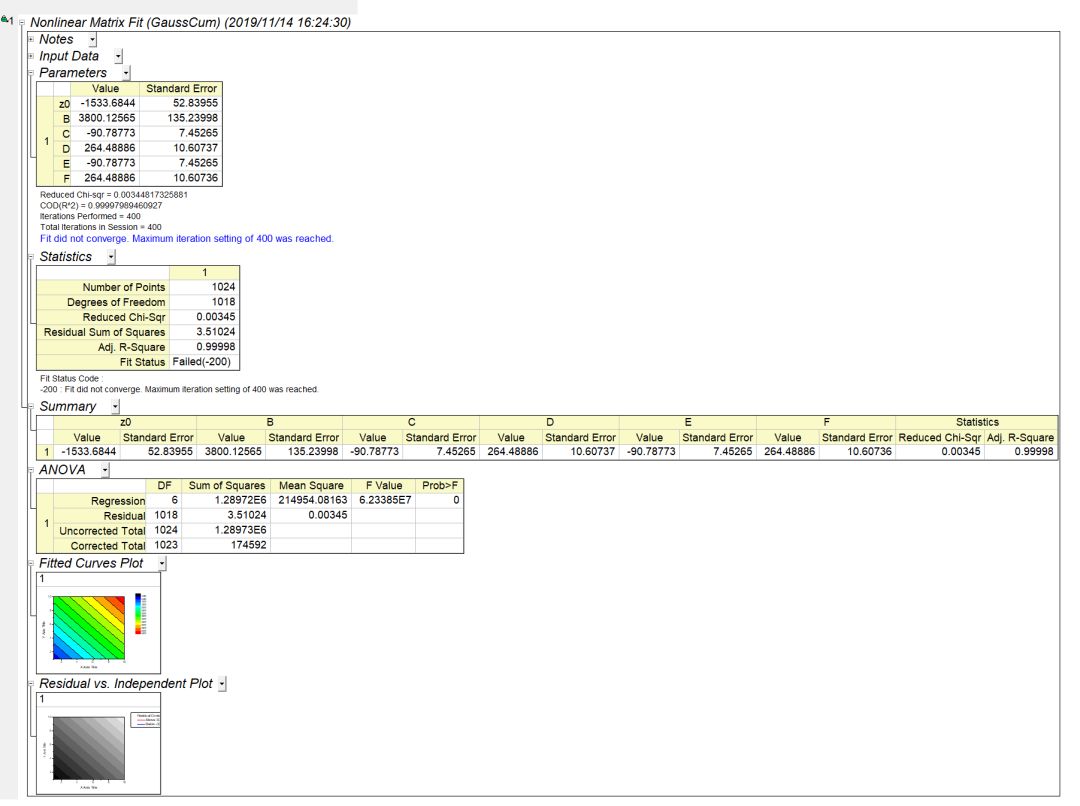图14  矩阵工作表数据非线性曲面拟合报表 如果对三维曲面进行拟合，该三维曲面必须采用 矩阵绘制 ，其拟合过程与上面一样，也是执行菜单命令Analysis一Fitting→Nonlinear Surface Fit。因为曲面拟合有两个自变量，因此散点图无法表示平面的残差，必须采用 轮廓图。 下面通过以实例数据文件转换的矩阵，来说明非线性曲面拟合。 (1)导入数据文件，并将其转换为矩阵工作表，如图15所示。根据转换后的矩阵表绘出图形如图16所示。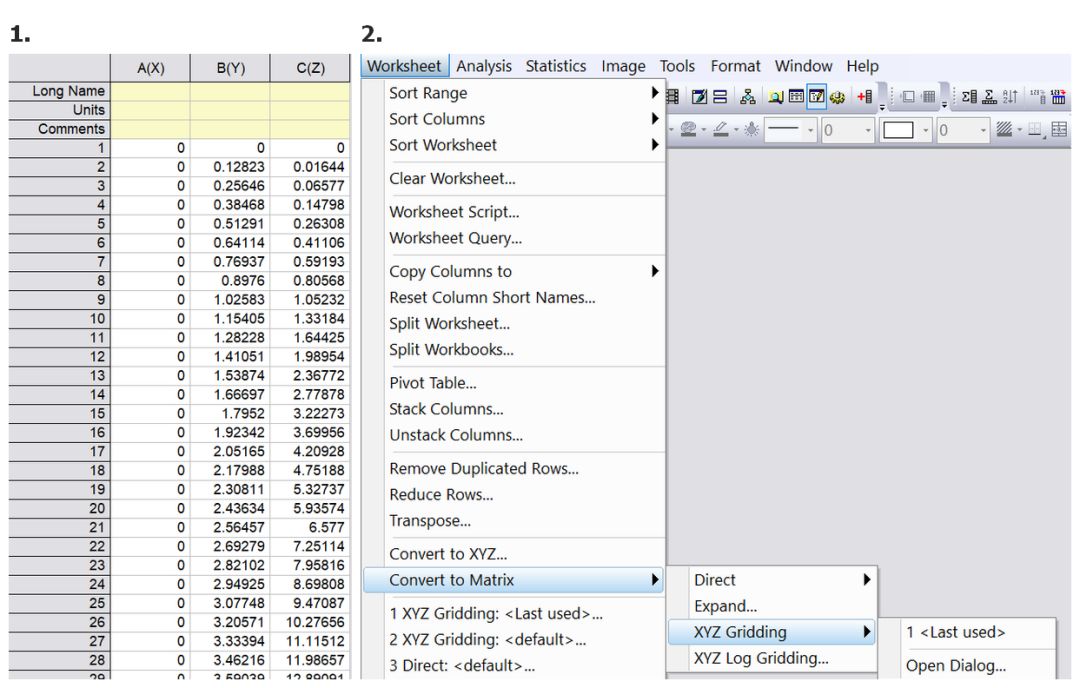 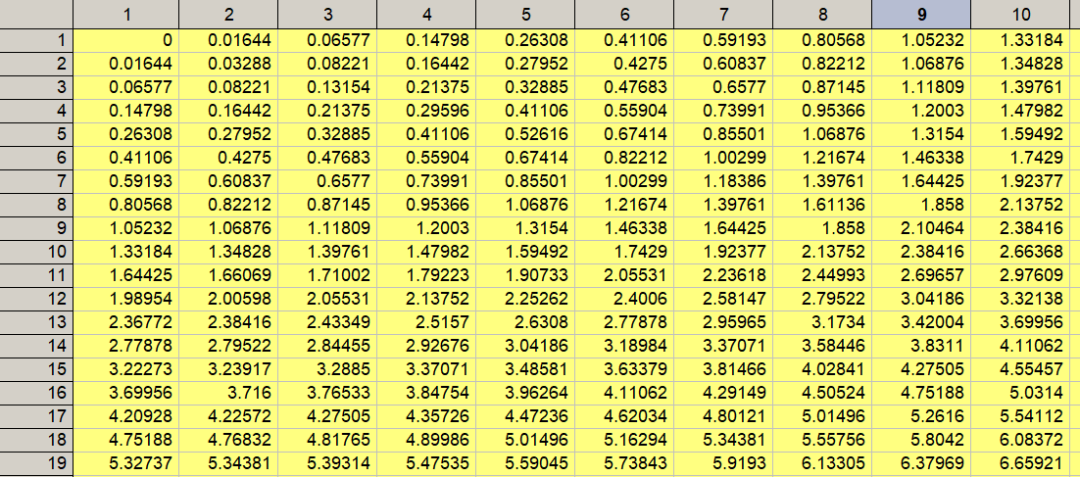图15 原始数据转化为矩阵工作表 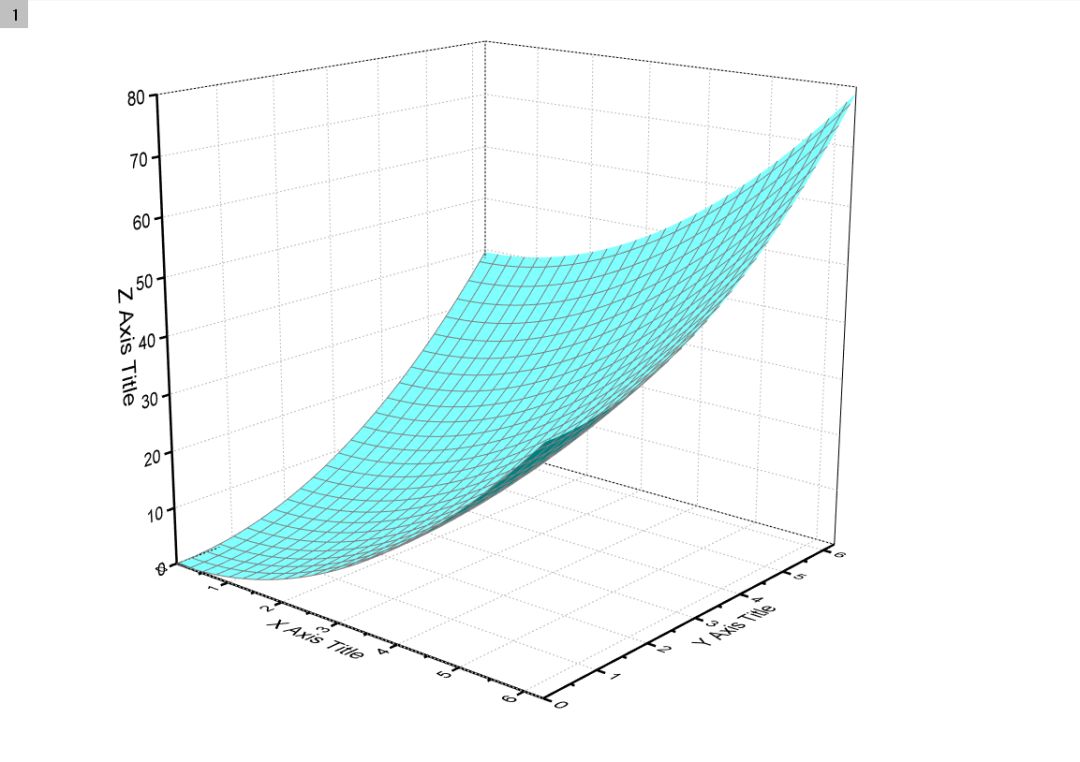图16 绘制图形 (2)将图16设置为当前窗口，执行菜单命令Analysis→Fitting→Nonlinear Surface Fit，打开NLFit对话框，选择“Lorentz2D”曲面函数，如图17所示。 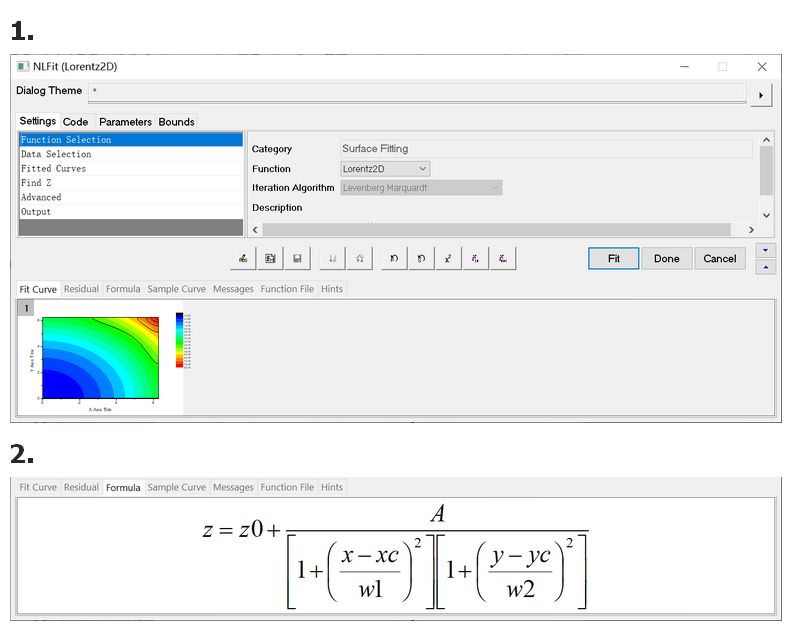图17 打开NLFit页面 (3)单击Fit按钮，完成曲面拟合，拟合得到的数据存放在新建的工作表中，如图18所示。 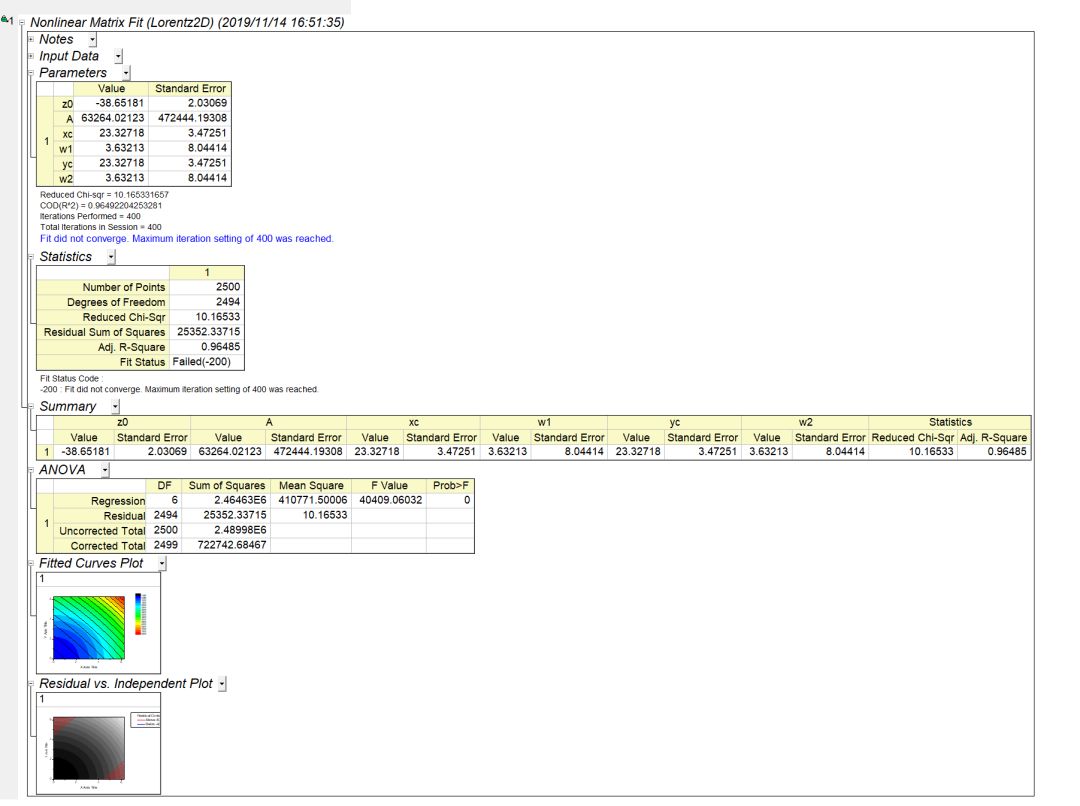图18 非线性拟合数据报表 把参数代入函数即可得到拟合函数。 这两篇都是利用origin内置的函数进行曲线拟合，虽然Origin in 内置的函数有200多个，然而实际使用时，我们会发现自己的拟合函数并不在内置中，这样就需要自定义函数进行曲线拟合。这个内容留待下次介绍，敬请期待！