Summary
正态总体均值的假设检验目的是推断总体均值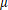 与
与 的大小关系,其中
的大小关系,其中 为已知常数。主要有如下三种假设:(1)
为已知常数。主要有如下三种假设:(1) (2)
(2) (3)
(3) 。在SPSS中,做上述3个假设的操作完全一样,结果的输出也完全一样,但是对输出结果中p值的解读却大不一样,稍微不慎就会得出错误的结论。本文将教你如何获取在不同假设下SPSS输出结果中的p值,内容分为:“举例”,“ P值的含义”,“ 假设(1)在SPSS中p值的读取”,“ 假设(2)在SPSS中p值的读取”,“ 假设(3)在SPSS中p值的读取”。
。在SPSS中,做上述3个假设的操作完全一样,结果的输出也完全一样,但是对输出结果中p值的解读却大不一样,稍微不慎就会得出错误的结论。本文将教你如何获取在不同假设下SPSS输出结果中的p值,内容分为:“举例”,“ P值的含义”,“ 假设(1)在SPSS中p值的读取”,“ 假设(2)在SPSS中p值的读取”,“ 假设(3)在SPSS中p值的读取”。
NO.1
举例
从甲地发送一个信号到乙地。设乙地接收到的信号值是一个服从正态分布 的随机变量,其中
的随机变量,其中 为甲地发送的真实信号值。现甲地重复发送同一信号5次,乙地接收到的信号值为:
为甲地发送的真实信号值。现甲地重复发送同一信号5次,乙地接收到的信号值为:
8.05 8.15 8.2 8.1 8.25,
设接收方有理由猜测甲地发送的信号值为8、大于8或小于8,问能否接受这3个猜测?(显著性水平 =0.05)
=0.05)
首先根据问题,分别作出相应假设:
(1) ;
;
(2) ;
;
(3) 。
。


从表1中可以看出 ,因此对于假设(1):
,因此对于假设(1): ,
, ,故拒绝原假设
,故拒绝原假设 ;假设(2):
;假设(2): ,首先判断出
,首先判断出 ,故
,故 ,故接受原假设
,故接受原假设 ;假设(3):
;假设(3): ,首先判断出
,首先判断出 ,故
,故
,故拒绝原假设 。
。
可以看出,上述3个假设中,p值的得出都来源于输出结果中的Sig,但是p值的获取以及p值与显著性水平 的比较方式却极为不同。但是,最后得出的结论却具有一致性,并不互相矛盾。你知道其中的原因吗?下面我们将详细讲解。
的比较方式却极为不同。但是,最后得出的结论却具有一致性,并不互相矛盾。你知道其中的原因吗?下面我们将详细讲解。
下面的讲解由于逻辑性较强显得有点枯燥,如果你不想仔细阅读,找到每一小节中的“划重点”也能知道原因哦~
NO.2
p值的含义
上述3个假设各自的内涵不同。假设(1)想要收集证据说明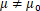 ,即证明
,即证明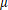 是
是
 的数;假设(2)想要收集证据说明
的数;假设(2)想要收集证据说明
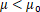 ,即证明
,即证明
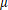 是一个远小于
是一个远小于
 的数;假 设(3)想要收集证据说明
的数;假 设(3)想要收集证据说明
 ,即证明
,即证明
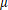 是一个远大于
是一个远大于
 的数。
而p值就是我们要收集的证据,第一个假设中的p值必须反映出
的数。
而p值就是我们要收集的证据,第一个假设中的p值必须反映出
 远离
远离
 的程度;第二个假设中的p值必须反映出
的程度;第二个假设中的p值必须反映出







 本文详细介绍了如何在SPSS中解读p值,针对正态总体均值的假设检验,分别讨论了p值在不同假设下的读取方法,包括假设(1)、(2)和(3),并结合实例解释了如何根据p值与显著性水平的关系做出正确的决策。
本文详细介绍了如何在SPSS中解读p值,针对正态总体均值的假设检验,分别讨论了p值在不同假设下的读取方法,包括假设(1)、(2)和(3),并结合实例解释了如何根据p值与显著性水平的关系做出正确的决策。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 4893
4893

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








