常用的收敛级数整理_一致收敛与收敛有什么区别？

最近看到这个问题，思考了很久，也看了很多的回答，我愚昧地以为许多都不是很接“地气”的回答。

对于刚刚接触数学分析，或者工科数学的分析的同学，我觉得二者最重要的区别，就在于两个字”过渡“。

可能读到这里的你会有疑惑，但是请向下继续阅读。

---

首先我们谈什么是“一致”？

这里首先梳理一下我们遇到的一致的概念：一致连续，一致收敛。

这里的一致是什么意思呢？

我们知道研究函数

在区间

上的连续性，只需要研究每个点上的连续性就可以了 . 对于

，给定误差

。只需要使得足够接近

的点

满足

，接近的程度我们一般用

来刻画 . 但是即使对于每个点

，都能够找到相应的

，也不能够说明：能否找到一个统一的接近程度

，使得只要

与

能有此接近程度，那么就会满足误差条件

也就是说，刚才我们研究单点的连续性时，需要找到一个

就行，但是现在我们要找到满足所有

的

. 如果这个

能够被找到，那么由于

满足所有的自变量

, 那么我们说这种连续性与自变量的位置无关，也就是说函数

在区间

上一致连续 .

下面来研究函数列或函数项级数的一致收敛问题 .

设函数列

定义在

上，这里

可以是任何区间 . 所谓的收敛实际上就是

时数列

是收敛的 . 根据收敛准则，任给误差

，存在

，当

时，成立

. 由于任意给定一个

，就能够找到一个符合上述条件的

，那么我们能不能找到对于所有

都适配的正数

呢？实际上我们取上面所有

的上界

即可

^[1] .但是有时候并不能尽如人意的找到 . 例如最简单的函数

在区间

上就不能够找到适配所有

的

，所以就不是一致收敛的了 .

---

这里我们看到，一致概念实际上针对的是变量的全体，就如一致连续和一致收敛的概念中所描述的那样 ，但是收敛就不存在这样的问题，例如函数列在单点处的收敛就退化为数列收敛的问题，就只有一个变量，这就不是困难的讨论了.

---

引入一致收敛的好处？

这里是本文的重点，前面已经提到过，一致收敛的好处在于”过渡“，这里的过渡指的是单独的函数的分析性质（连续，可导，积分）向 和函数 的分析性质的过渡 .

在数学分析的教材上，和函数的连续，可导，积分的性质都要有一个前提的条件：一致收敛 . 正是有了一致收敛作为桥梁，才能够使得每个函数的连续性，可导性与积分性质推到和函数上，这实际上是有限函数求和所得到的和函数性质所不需要的条件。（有限个连续 ，可导， 可积分函数的和也是连续，可导，可积分的) .

笔者本人整理的讲义部分

---

.

高等数学或者数学分析，大部分时间都花在了函数性质的讨论上，而函数项级数的一致收敛告诉我们，如果能够先知道一致收敛性，我们就能够从单个函数直接得到和函数的性质 .

正如我们研究 傅里叶级数 时不正用到了函数项级数的一致收敛吗？

---

一致收敛几何上的表示

下面两个题目中的函数图像告诉我们，函数列在不一致收敛点处的图像是”突出的，不平稳的“^[2].

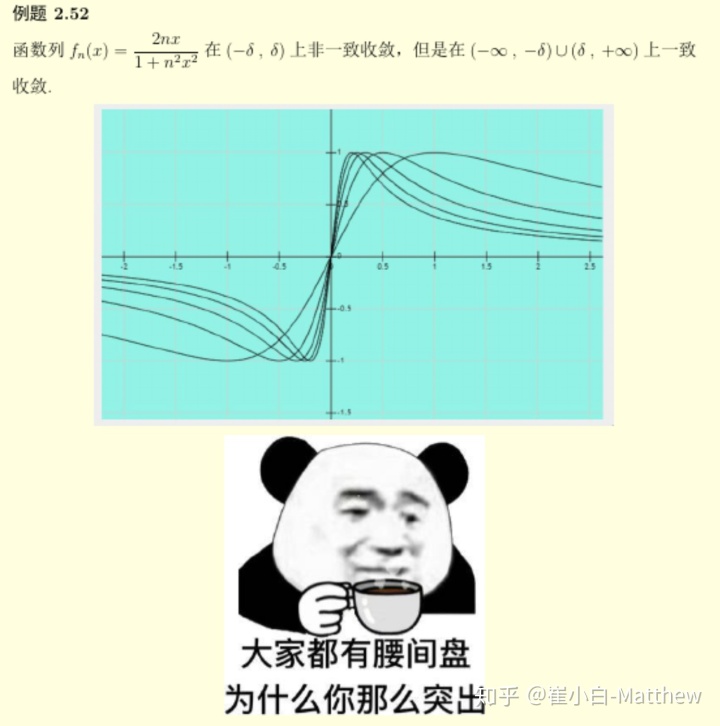
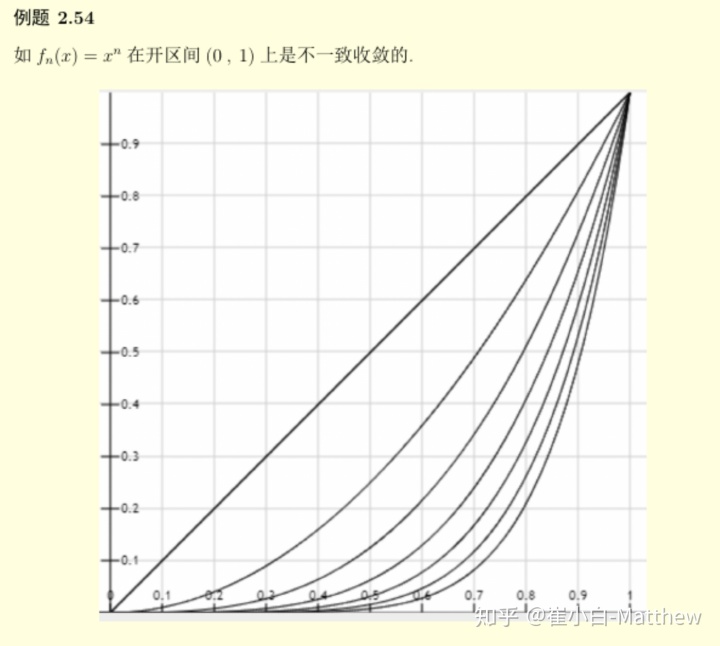
从图像上的现象可以总结出下面判断函数列一致收敛的定理

函数列

在区间

上一致收敛的充分必要条件是

这里

描述的是函数

”最突出“的地方有多高，当在极限过程中，”最突“的地方”不突“了，那么就可以判断是一致收敛的了 .

---

转载请注明出处，谢谢！

参考

1. ^这个符号仅用于解释说明概念，不是正规符号
2. ^意会即可 .