c++ 判断 directx 加速不可用_轻绳连接体的速度和加速度

本文第一作者：黄晶

在中学物理竞赛训练题和大学物理力学题目中，有一类轻绳连接体问题，求绳上连接体速度和加速度关系。最典型的是绳拉小船问题[1-3]，人以恒定速率拉小船，那么小船的速度和加速度是多少？还有1类题目是多个物体通过滑轮和绳子相连，运动过程中轻绳始终保持绷紧，那么这些连接体的速度以及加速度有什么关系?[4-6]。一个常见的结论是，如果只有两个物体，那么这两个物体在绳子方向上的速度分量大小相等，但加速度分量大小不一定相等[4]，不可能同时为零[5]。对于多个物体, 绳子两端速度差在绳子方向上的投影(分量)之和为零, 加速度也如此,前提条件是绳子方向不变[6]。解决这类连接体速度和加速度问题, 中学物理竞赛辅导读物上主要是应用加速度分解法和投影法，但这种二级结论需要前提条件，即两物体的距离不变。我们发现，简单利用力学定义概念和求导计算，就能得到一般的结论，且能简化并推广一些所谓的物理难题。本文主旨并不是要求中学生记住文中公式并用来解题，而是给出处理这种难题的另一种思路，开阔他们的视野。

1 引理

首先证明一个结论，取合适的坐标系，设物体都是小环, 在绳上能自由移动。第i个物体的坐标是ri(t)，离它最近的静滑轮(可能有两个，所以有两个下标)坐标是qij, 如图1所示。

图1 多个物体(小环)通过滑轮和绳子连接

运动过程中绳子始终保持绷紧，绳子总长度是时间的函数

(1)

这个约束条件对时间t求导一次和两次，就能得到各个连接体速度和加速度关系式。利用以下结论

(2)

定义物体相对最近静滑轮单位方向为

(3)

式(1)两边对时间求一次导数，计算化简得到

(4)

式(4)意味着各个连接体速度沿相对最近静滑轮方向分量之和为绳子总长伸缩的速度。如果只有两个物体，且绳子总长度不变，那么两个物体在绳子方向上的速度分量大小相等。式(4)两边继续对时间求导，计算化简得到

(5)

那么式(5)的物理意思是什么呢？式(5)左边是各项相加，每一项有两部分。第一部分是，物理意义就是第i个物体加速度在相对最近定滑轮方向上的投影(分量)，即径向加速度(大小)。第二项是两个量的比值，分母|ri(t)-qij|是第i个物体到最近静滑轮的距离，分子是两项速度平方之差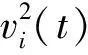，是第i个物体速率的平方，即总速度大小的平方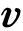，(i(t)·nij)2是物体第i个物体速度在相对最近定滑轮方向上的投影(分量)的平方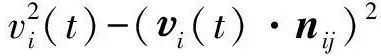的物理意义就是第i个物体垂直相对最近滑轮方向速度分量(法向速度)的平方。以最近静滑轮为参考点，法向速度的平方比上径向距离，这个就是我们熟悉的向心加速度(大小)的定义。式(5)也就意味着所有物体相对最近滑轮的径向加速度(大小)和向心加速度(大小)之总和为绳子总长伸缩的加速度。如果只有两个物体通过一个不可伸长的绳子连接，式(5)化为

(6)

式(6)就是不少物理竞赛辅导读物上的所谓加速度投影法，前提条件是两点之间的距离不变。如果只有一个物体通过一个不可伸长的绳子联系，式(5)化为

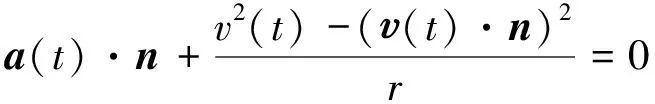
(7)

式(7)就是物理教材上物体做圆周运动径向加速度和向心加速度的关系式。

2 应用

第1节的式(4)和式(5)可以用来求解绳连接物体速度，加速度和绳中张力问题。先取定一个直角坐标系，把各个物体的速度和加速度，以矢量的分量形式表示出来，然后代入式(4)和式(5)，利用已知条件，求未知量。下文中的3个例子,都是中学物理竞赛辅导读物中的经典例子, 为了讨论方便, 拉绳速度和杆转动角速度都是匀速的, 没有进一步去考虑加速度和角加速度。我们作了推广,考虑到这两个因素, 给出主要推导过程，不过没有给出各个物体速度和加速度的最终表达式。如果把一些几何和物理量取特殊值或者容易计算的值，就能改变为中学生物理竞赛模拟题。

2.1 转动杆连线模型

第一个是文献[4]中的问题，杆的长度是L，杆是变速转动的。如图2所示(来自文献[4])物体C和物体A(杆的端点)，通过一个绳子和静滑轮联系起来。设B处滑轮为原点，水平方向为x轴，垂直向上的方向是y轴。此时角速度是ω，角加速度是χ。物体C的速度是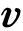C=(0,v)，加速度是aC=(0,a),相对最近定滑轮的单位方向是nC=(0,-1)。物体A的速度是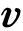A=ωL(cosα,-sinα),加速度是切向加速度和法向加速度的矢量和aA=χL(cosα,-sinα)-ω2L(sinα,cosα),相对最近定滑轮的单位方向是nA=(sinθ,-cosθ)。把这些速度和加速度的表达式代入到式(4)和式(5)，再利用△ABO边长和角度关系，计算得到物体C的加速度大小是

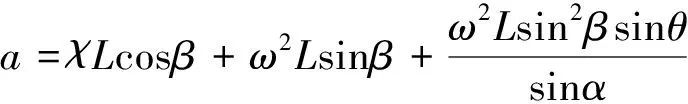
(8)

2.2 两物体一滑轮模型

第二个例子来自文献[7],在竖直墙上同一高度钉两个钉子，左边钉子上系一根不可伸长的轻线，线上内套一个有质量的小环，线的另一端跨过右边钉子，在线的自由端上挂一个物体，如图3所示。在开始位置，两个钉子之间线呈水平，小环处于线上任意位置，小环和物体初速度为零。求小环经过最低点时的加速度。这个问题中，右边钉子看作静滑轮。文献[7]中的原题是经过平衡位置，但平衡位置是否能到达，与初始条件有关，另文探讨。

设小环质量为m1，物体质量为m2。两个钉子间的距离是l。小环竖直方向上下降距离h, 达到最低点时，左边绳子长度是l1，与水平方向夹角是α，右边绳子长度是l2，与水平方向的夹角为β。以水平方向为x轴，垂直向上的方向是y轴。当小环滑到最低点时，小环的速度为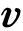1=(v,0)，加速度为a1=(a1x,a1y)，相对最近两个滑轮的单位方向分别为n11=(cosα,-sinα)，n12=(-cosβ,-sinβ)。物体的速度为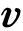2=(0,u)，加速度为a2=(0,a2y)，相对最近滑轮的单位方向为n2=(0,-1)。代入连接体的速度关系式(4)，计算得到

(9)

还需要一个条件来确定两个物体速度的值，这个条件就是机械能守恒：

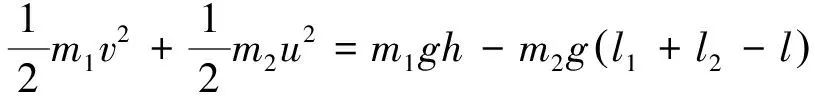
(10)

由式(9),式(10)可以求出小环达到最低点时两个物体的速度。把以上的速度和加速度表达式代入式(5)，得到

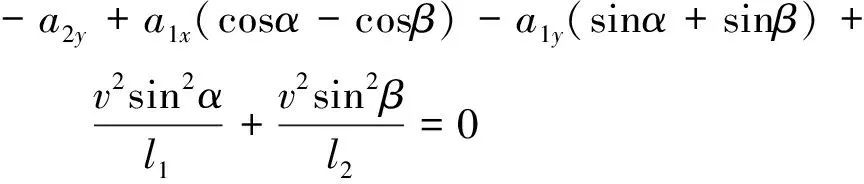
(11)

式(11)中有3个未知量，小环的两个加速度分量和物体的竖直方向的加速度，还需要找到另外两个方程。看起来找不到，不过考虑到绳子中张力，两个物体贡献3个牛顿第二定律方程，小环水平和竖直方向和物体竖直方向。这样4个未知量，4个方程，就能解出来了。设小环达到最低点时，绳子中的张力为T, 那么由牛顿第二定律，可以得到以下3个方程：

联列求解式(11)～(14)，就能得到绳子中的张力T和物体的加速度。

2.3 绳拉物体模型

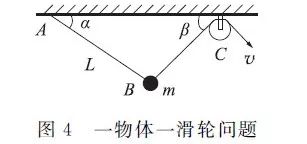
第三个例子来自文献[8]，如图4所示。有一个质量为m的质点B，一端通过长度不变的绳子系在A点，另一端通过长度变化的绳子绕过C点的滑轮。A、C位于同一水平线上。某人握住绳的自由端，以随时间变化的速率v(t)收绳，当绳收至如图位置时，质点B两边的绳子与水平线的夹角分别为α和β，求这时人收绳的力。

AB之间的绳子长度不变，BC之间绳子长度在变化，这样式(4)和式(5)要各用两次。设物体B的速度是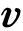=(v1,v2)，加速度是a=(a1,a2)，相对A点的单位方向是nA=(cosα,-sinα)，相对C点的单位方向是nC=(-cosβ,-sinβ)。代入到连接体的速度关系式(4)，计算得到

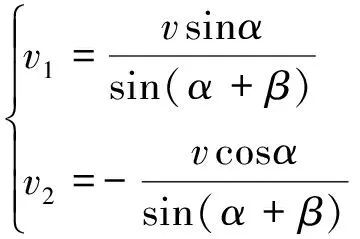
(15)

代入连接体的加速度关系式(5)，计算得到

(16)

(17)

由式(16)～(17)，可以求得物体B的加速度。设AB和BC两个绳子上的张力分别为T1和T2，那么由牛顿第三定律，得到

由式(18)～式(19)，可以求得两个绳子中的张力。

3 结语

对于轻绳连接体的速度和加速度, 中学物理和大学物理的处理方式不一样。中学主要是利用一些二级结论, 对各个问题作具体分析, 需要很强的技巧性, 譬如区分相对那个物体的切向和径向(加)速度, 然后叠加起来。不过有些二级结论是有前提条件的, 不分析清楚就用,会出现问题的。大学物理则是假设物体的速度和加速度存在(一般在直角坐标系中), 然后代入到约束关系以及它的后续关系中, 再计算得到这些(加)速度的值, 基本不需要技巧性。不过本文第2节中3个例子, 都是讨论特定位置或者特定时刻物体的(加)速度和绳中的张力, 如果要讨论整个运动过程中这些物理量随时间的变化关系, 即从特殊情形到一般情形, 就要用分析力学中的一些知识。以本文3个模型为例, 写出体系动能和势能表达式, 体系的拉氏量就是动能减去势能。几何约束关系乘以一个拉氏因子(物理意义是绳中张力), 加入到拉氏量中去。由拉氏量得到拉氏方程, 加上初始条件，数值求解这些微分方程,就能得到整个过程中物体(加)速度和绳子张力随时间变化的表达式。限于篇幅，不再详述。

参考文献

[1] 钱树高, 夏英齐. 船的加速度和速度佯谬——再论用绳拉船靠岸的问题[J]. 物理与工程, 1999(2):14-15.

QIAN S G, XIA Y Q. The paradox of velocity and acceleration of ship—Think again about the problem of pulling the ship to the shore by rope[J]. Physics and Engineering, 1992(2): 14-15. (in Chinese)

[2] 程达三, 刘兴来. 也谈“用绳拉船靠岸的船速问题”[J]. 物理与工程, 2000(4):29-32.

CHENG D S, LIU X L, Again on the problems of ship’s velocity pulled to the shore by rope[J]. Physics and Engineering, 2004(2): 29-32. (in Chinese)

[3] 钱树高, 夏英齐. 用绳拉船和速度的合成与分解[J]. 物理与工程, 2009, 19(2):55-60.

QIAN S G, XIA Y Q. Pulling the ship by rope and the composition and decomposition of velocity[J]. Physics and Engineering, 2009,19(2): 55-60. (in Chinese)

[4] 陆天明.对一道沿绳加速度问题的深入研究[J]. 物理教师，2014， 35(7): 95-96.

LU T M. Father study on the acceleration along the rope[J]. Physics Teacher, 2014， 35(7): 95-96. (in Chinese)

[5] 冯明志. 加速度能同时为零吗？[J]. 物理教师，2008， 29(1): 57-58.

FENG M Z. Can the accelerations reach zeros simutanepusly?[J]. Physics Teacher, 2008， 29(1): 57-58. (in Chinese)

[6] 于希梅, 毛安君. “绳连接”问题的运动学公式[J]. 物理与工程, 2012, 22(5):6-7.

YU X M, MAO A J. The kinematical formula of linked objects model[J]. Physics and Engineering, 2012,22(5): 6-7. (in Chinese)

[7] 袁张瑾，俞骁翀. 俄罗斯中学物理赛题新解500例[M]. 杭州：浙江大学出版社，2008，65-66.

[8] 程稼夫. 中学奥林匹克竞赛物理教程-力学篇[M].合肥：中国科学技术大学出版社，2005：42.

基金项目: 浙江省十三五师范教育创新工程。

作者简介: 邱为钢, 男, 湖州师范学院求真学院公共教研部副教授，主要从事大学物理的教学研究工作，wgqiu@zjhu.edu.cn。

引文格式: 黄晶，邱为钢. 轻绳连接体的速度和加速度[J]. 物理与工程，2018，28(6)：32-35.

END

更多精彩文章请点击下面“蓝字”标题查看：

• 第五届全国高等学校物理基础课程青年教师讲课比赛第一轮通知

• 2018年全国高等学校物理基础课程青年教师讲课比赛决赛点评——王稼军教授在比赛颁奖典礼上的讲话整理稿

• 潘小青、马世红：首届全国高校物理实验青年教师讲课比赛后的思考

• 祝贺《物理与工程》再次入选中国科技核心期刊！

• 2018-2022年教育部高等学校大学物理课程教学指导委员会成立会议暨第一次工作会议在北京举行

• 王亚愚教授：清华物理系本科人才培养理念与实践

• 朱邦芬院士：“减负”误区及我国科学教育面临的挑战   

• 朱邦芬院士：遏制学术不端，从认真查处重大案例开始

• 朱邦芬院士：从基础科学班到清华学堂物理班

• 朱邦芬院士：为什么浙江省高考学生选考物理人数大幅下降值得担忧

• 朱邦芬院士：回归后杨振宁先生所做的五项贡献

• 朱邦芬院士：对培养一流拔尖创新人才的思考

• 王青教授：小班教学与翻转课堂：《费曼物理学Ⅱ》的10年教学实践——纪念费曼先生百年诞辰

• 安宇教授：为什么传统的课堂讲授模式需要改变

• 王青教授：理解经典电磁学理论

• 日本高等物理教育近况

• 龙桂鲁、王新：自由落体东移的简单说明

• 葛惟昆教授：关于中外人才培养的几点思考

• 王祖源、张睿：基于SPOC的大学物理课程混合式教学设计与实践

• 孟卫东、何龙：基础教育领域综合改革之考试改革的现状及改进建议

• 包景东教授：费恩曼的10大贡献及教学启示

• 第四届“高等教育杯”全国高等学校物理基础课程青年教师讲课比赛决赛成功举行

• 2013—2017年教育部高等学校大学物理课程教学指导委员会工作总结

• 2018年高等学校物理基础课程青年教师讲课比赛 六大赛区获奖名单

• 《物理与工程》“新工科建设”栏目开张啦

• 美国大学先修(AP)物理课程分析

《物理与工程》期刊是专注于物理教育教学研究的学术期刊，是中国科技核心期刊，1981年创刊，欢迎踊跃投稿，期刊投审稿采编平台：

http://gkwl.cbpt.cnki.net

欢迎关注

《物理与工程》微信公众号