cholesky分解_[数值计算] QR分解

0. 为什么要用QR分解

的问题可以分成3类：

• 情况1：A是方阵，m=n
• 情况2：A是over-determined的，m>n
• 情况3：A是under-determined的，m<n

在[数值计算] 条件数的例子2里，遇到的情况1（A是方阵），通过构造拉格朗日插值来使得对A求逆足够稳定。对于一般的情况下，解决思路是使用LU（LUP）分解来解决稳定性问题，在前一篇文中已经简介过了[数值计算] LU分解、LUP分解、Cholesky分解。

对于后两种情况， [数值计算] 数据拟合——线性最小二乘法 分析了用正规方程组求解over-determined以及under-determined的问题。但在文中也提到了，对于over-determined的线性最小二乘问题，正规方程组是不稳定的，通常需要用QR分解来处理：

理论很美好，在小数据量的时候没问题，然而直接使用正规方程组求解会在数据量大(e.g. data size > 100)的时候不稳定numerically unstable。原因是 需要对

求逆，而A我们都知道是Vandermonde矩阵的一部分，本身就是poorly conditioned，而

只会更糟糕。解决的方法是使用

QR分解，这也是Python MATLAB求解 线性最小二乘 问题的方法。

1. QR分解

1.1 定义

一个矩阵

可以被分解成

，其中：

• 是正交矩阵
• 是上三角矩阵

1.2 正交矩阵的性质

• 左乘一个正交矩阵对欧式范数的结果不影响（在下面证明eq.2的时候会用到）

1.3 从QR分解角度看线性最小二乘

对于一个over-determined线性最小二乘问题

，其目标函数是

这里

，

，

，

。

如果把

拆分成上下两部分，形式

类似，

。那么目标函数可以写成下面的形式：

可以看到，我们只能最小化前一部分

到0，即

，

的最小值为

。这样处理之后就避免了求正规方程组中的

，避免了条件数变成

，所以QR分解法更加数值稳定。

1.4 计算QR分解的方法

一共有三种：

• Gram–Schmidt Orthogonalization
• Householder Triangularization
• Givens Rotations

1.5 Gram–Schmidt Orthogonalization

1.5.1 Reduced QR分解

GSO构建正交矩阵

的方法是从A矩阵的n个列（

）中构建互相正交的基，先选定

为第一个基，然后把第二列

减去平行于

的部分，剩下的垂直于

的部分作为下一个基，以此类推，直到生成了n个基。

这个方法生成的

，

，和section1.1中定义的Q是方阵，R不是方阵有区别。这个结果被称为Reduced QR分解，因为m>n，所以只满足

，而不满足

。

Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

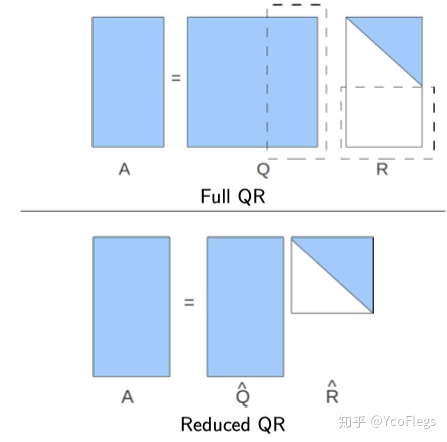
Reduced QR分解同样可以求解over-determined线性最小二乘问题。形式类似Full QR分解：

其中

，

。

1.5.2 Full QR分解

为了实现定义中的完整的QR分解，需要把上面生成Q中的n个基拓展成m个互相正交的基。但此处并没有对额外的m-n个基的顺序有特殊要求，因此任意一种顺序都可以。另外还需要把

下面加m-n行零矩阵。

在Python中，Reduced QR分解和Full QR分解对应于

q

1.5.3 Classic Gram–Schmidt Orthogonalization算法 CGSO

观察Eq.4可以发现，其实每一步迭代都只有一个

未知：左边

已知，右边

已知， q的系数们

可以用公式

求得。把

代入Eq.4，并整理可得

因此

，

。其中，

的符号不确定是因为，任意一个基方向反向之后，这个QR分解不会有任何问题，这个基仍然和其他基正交。为了计算方便，这里就规定

。

整理上面计算

和

的过程为算法的形式：

Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

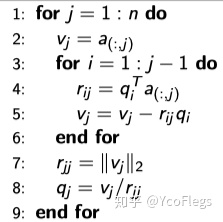
观察算法过程，可以发现，唯一可能在理论上出问题的情况就是，出现某个

=0，导致在算法第8行出现0在分母上的情况。因此只要

是满秩的，且每个

都>0，那么reduced QR分解的结果是唯一的。

1.5.4 Modified Gram–Schmidt Orthogonalization算法 MGSO

由于CGSO对舍入误差很敏感，容易导致生成的基

的正交性随着迭代越来越弱，因此引入改进的GSO。核心思想是，在每个

生成后，直接把A剩下的列（下面算法第7行）都去掉

的成分（下面算法的第8-9行）。因为只是把计算的顺序变了，所以理论上计算结果是一样的。

Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

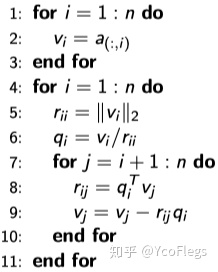
但是改进之后稳定性会好很多。从实际计算步骤上来看，CGSO和MGSO的区别在于，CGSO中，每次迭代新的一列

，计算每个

都是用的同一个

，而MGSO计算

的时候用的

是已经减去前面j-1个基的分量之后的

。

这样做的好处是：误差的传递是局部的。比如计算

是精确的，计算

出现误差，即，

在

上存在一个微小分量。按照CGSO，接下来要分别计算

在

和

的分量，最终

；而MGSO则先计算

在

上的分量，去除掉这个分量之后成为

，再计算并去除

在

上的分量得到最终的

，此时如果计算是精确的，那么至少可以保证

。

直观理解参考下面这张图，在三维xyz坐标系里，

是带误差的

。用CGSO处理

的时候，

用的是初始值

，包含了

和

两个方向的误差，而用MGSO处理

的时候，

用的是去掉

分量之后的

，只有

方向的误差。

公式上计算这些误差参考The modified Gram-Schmidt procedure：

Credit to https://www.math.uci.edu/~ttrogdon/105A/html/Lecture23.html

1.6 Givens Rotations

1.6.1 Givens Rotation Matrix

1.6.2 Givens Rotations的作用

对于一个矩阵

，对于第i列的第j和k行

，如果

元素不为0，可以通过一个Givens Rotation把它转换成0。

当

或者

很小或者很大，且它们的平方不是用float表示的时候，对它们求平方会导致上溢出或者下溢出。因此更好的公式是：

• 如果
  ，那么设

• 如果
  ，那么设

不过这个问题基本只有在设计package造轮子的时候才会遇到，所以通常用Eq.10不会引起问题。详见Scientific Computing - Heath的第128页。

另外，在涉及反三角的数值运算的时候，建议使用atan2替代atan，范围更大，更稳定。例如atan2(y,x)会返回一个(x,y)向量和正x轴的夹角。

the difference between atan and atan2 in C++?​stackoverflow.com

wikipedia Atan2​en.wikipedia.org

1.6.3 Givens Rotations 算法

对于一个稠密的矩阵

，逐渐把A消元成R（参考1.5.1的full QR的图）。

Credit to http://iacs-courses.seas.harvard.edu/courses/am205/schedule/

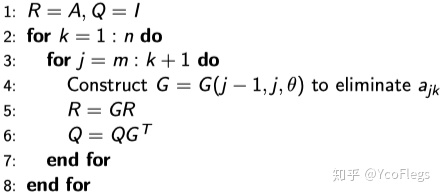
注意第三行的循环，j是从大到小的迭代。

1.6.4 Givens Rotations 优势

当A是稠密矩阵，Givens Rotations并没有比另外两种算法更高效，但如果A是稀疏矩阵，那么Givens Rotations大小为0的元素可以直接被忽略。另一个优势是，Givens Rotations更容易并行化，因为Givens Rotations只对两个元素进行操作，处理不同列的时候可以完全的独立。