因果论（二）概率论基础（贝叶斯网络）

最新推荐文章于 2024-08-14 22:29:49 发布

第六五签

最新推荐文章于 2024-08-14 22:29:49 发布

阅读量248

点赞数

分类专栏：因果论文章标签：人工智能

本文链接：https://blog.csdn.net/weixin_39699362/article/details/131886889

版权

因果论专栏收录该内容

5 篇文章 6 订阅

订阅专栏

文章介绍了图的概念，包括顶点和边，以及它们在表示变量关系中的作用。接着，它详细阐述了贝叶斯网络，特别是马尔科夫父代变量集合的概念，以及如何用有向无环图(DAG)来表示变量间的依赖关系。此外，文章还提到了d-分离准则在检验变量独立性中的重要性。

摘要由CSDN通过智能技术生成

一、图

图由顶点集( 或节点集)V 和连接顶点E的边集( 或链接集) E 组成。图中的顶点对应于变量（因此使用相同的符号V) , 边表示变量对之间的某种关系，具体何种关系因应用的不同而变化。由边连接的两个变量称为相邻变量。

图中的每条边可以是有向的（由边上的单个箭头表示），也可以是无向的（无箭头链接）。在某些应用中，我们也会使用"双向 ” 边来表示未观察到的共同原因（有时称为混杂因子）。

二、贝叶斯网络

图在概率与统计建模中的作用有三个方面:

1. 提供便捷的方法来表示众多的假定

2. 便于联合概率函数的简约表示

3. 便于从观察中进行有效推断

定义1.马尔可夫父代变量集合

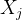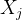令 $V={X_{1},X_{2},...,X_{n}}$ 表示有序的变量集合，令P(v)表示这些变量的联合概率分布，如果 $PA_{j}$ 是使 $X_{j}$ 独立于其他前驱变量的极小前驱变量集合，那么变量集 $PA_{j}$ 称为 $X_{j}$ 的马尔科夫父代（变量）集合。换句话说， $PA_{j}$ 是满足公式（1）的 ${X_{1},X_{2},...,X_{j-1}}$ 的子集且 $PA_{j}$ 的任何子集均不满足公式（1）

$P(x_{j}|pa_j) = P(x_{j}|x_{1},x_{2},...,x_{j-1}))$ (公式1)

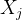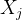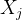定义1给出了贝叶斯网络的构造方法。定义1 为每个变量 $X_{j}$ 分配一个足以确定 $X_{j}$ 概率的前驱变量集合 $PA_{j}$ 。一旦我们获知父代集合 $PA_{j}$ 的取值后，获悉其他先驱变量的值就变得冗余。这种分配可以用 DAG 的形式表示，其中变量由节点表示，并从父节点集 $PA_{j}$ 的节点到节点 $X_{j}$ 也引入箭头。我们可以采用递归的方式进行构造。

比如：有概率联合分布（对应图的蕴涵分解） $P(x_{1},x_{2},x_{3},x_{4},x_{5}) = P(x1)P(x_{2}|x_{1})P(x_{3}|x_{1})P(x_{4}|x_{2},x_{3})P(x_{5}|x_{4})$

根据 $P(x_{2}|x_{1})$ 可以确定（x1,x2）相关，可以画出x1指向x2的有向子图；

根据 $P(x_{3}|x_{1})$ 可以确定（x1,x3）相关，可以画出x1指向x3的有向子图；

根据 $P(x_{4}|x_{2},x_{3})$ 可以确定（x2,x4）和（x2,x4）相关，可以画出x2指向x3和x2指向x4的有向子图；

根据 $P(x_{5}|x_{4})$ 可以确定（x4,x5）相关，可以画出x4指向x5的有向子图；

最终画出的有向无环图如下图所示。

定义2：如果概率函数P容许有向无环图G有形如公式（1）的分解，那么我们认为G表示P，G与P相容，P与G马尔可夫相关。

在统计建模中，确定 DAG 和概率之间的相容性非常重要，主要是因为相容性是有向无环图G 解释 P 表示的经验数据（即描述一个产生 P 的随机过程）的充分必要条件。

定义2：d-分离准则

考虑 3 个不相交的变量集X 、Y 和Z , 它们表示有向无环图 g 中的节点集。为了检验在任何与g 相容的分布中在Z 条件下X 是否独立于Y , 我们需要检验变量集 Z 所对应的节点是否"阻断 ” 了从节点 x 到节点 y 的所有路径。这里的路径是指图中一系列连续的（任意方向的）边，阻断可以解释为阻止这些路径连接的变量之间的信息流（或关联流）。

正如下面所定义的。