考虑个离散联合分布的随机变量,根据条件概率分布,我们知道,联合分布概率可表示为:
(1)
设每个变量有个值,那么要求某个变量
的概率取值,则要对其他所有变量求和,即
(2)
对于变量有个值的情况,该问题的复杂度是
,显然复杂度非常高,实际应用中是不可行的,考虑另一种极端情况,即所有变量都是相互独立的,那么这个时候只需单独求
,也就是我们通常使用的朴素贝叶斯的方法。贝叶斯网络的方法介于两个极端之间,即每个变量的变化都依赖于其他所有变量的一个子集,此时联合概率分布可以表示为:
(3)
这里,对应与变量
相关的变量集合,其为全体变量集合的一个子集,例如
(4)
公式(4)对应的贝叶斯网络结构为:

即,
,
,
,
,
。集合
称为变量
的父集合,从统计学的角度来看,如果给定父集合的值,那么变量
统计独立于集合里所有其他变量,每一个
都表示了一种条件独立的关系,其给出了一个蕴含在多元集合中的概率结构,由于其相互独立的特性,我们可以利用此特性降低计算复杂度。
1.图的基本定义图的定义一般用表示,
为节点,
表示节点间的互联关系即图的边,每一个成员都是一对连接关系(也就是一条边)
,一条边可以是有方向(表示为
)的,也可以是无方向的,一条边将两个节点连接起来,如果结点
可以通过一些列边连接到
,那么我们称这些边组成的序列为
到
的路径(path),如果一条路径起终点为同一个节点,我们称之为循环(cycle)。有向图是指只包含有向边的图结构,若其结构内不存在cycle,那么称之为有向无循环图(directed acyclic graph,DAG),如果
可以通过一条路径连接到
,那么
称为
的祖先,否则则为非祖先,如果存在一条边(有方向的)从
到
,那么
称为
的父节点,
称为
的子点。这里要注意区分祖先节点和父节点地区别。
贝叶斯网络结构是一个DAG,其节点代表随机变量,其任一节点变量
关于父节点集合条件独立于所有非祖先节点,这通常也被称为马尔科夫条件。这就是贝叶斯网络的基本定义,这里给出条件独立的定义:如果
或者等价地
,则称事件
和
对于给定事件是
条件独立的,也就是说如果
发生时,
发生与否与
无关。需要注意一点条件独立和独立是不存在蕴含关系的。
那么基于此,下面介绍两个比较重要的定理:
定理1:为一个贝叶斯网络结构,
为该图结构所有节点对应随机变量的联合概率分布,那么
就等于所有节点关于父节点条件分布概率的乘积,通常称之为
可以因式分解(factorizes over)于
。且该定理反过来说也是正确的。
定理2:图为一个DAG,每一个节点都具有关于父节点的条件概率,那么这些条件概率的乘积得到了变量的联合分布,并且其满足马尔科夫条件。该定理是很有用的,因为在实际中,这通常是我们构建概率图模型的方式,对于我们要模型化的物理过程,使用推理的方法分层构建,并在图模型中编码条件独立关系。
我们对比下定理1和定理2,定理1假定了一种分布,基于潜在的条件独立建立了贝叶斯网络,定理2与之相反,基于网络结构,解释了每个节点的分布特性。
举一个例子:我们现在来研究一个国家的GNP与其教育水平、成年人工作类型的关系。为GNP,取2个值HGP和LGP分别对应高(high)和低(low)GNP;
为教育水平,取3个值NE、LE和HE分别表示未接受教育、低水平教育和高水平教育;
为工作类型,取3个值UN、LP和HP,分别对应无工作、低收入和高收入。使用足够多的样本,可以学习到如下概率:
1.边际概率:
![]()
2.条件概率:


可以看到,即使简单的3个变量,也需要17个概率值。考虑贝叶斯网络图如下:
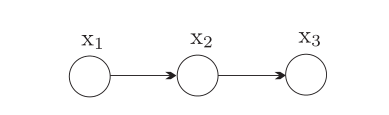
马尔科夫条件认为,给定的情况下,
和
不相关(工作的好坏取决于教育情况而与国家GNP无关,这里只是假设,不要杠)。下面我们验证一下贝叶斯网络是满足马尔科夫条件的,根据定理1,联合概率可以表示为:
也就是说,如果一个人来自富有的国家,接受过高等教育,拿到较高薪水的概率为:(0.8)(0.75)(0.2) = 0.12,类似的,一个人来自贫穷国家,接受教育水平较低,收入低的概率是: 0.476。下面可以验证下,贝叶斯网络结构是满足马尔科夫条件的,考虑:
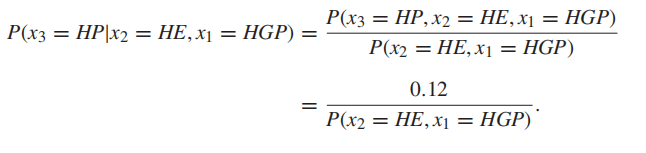
并且
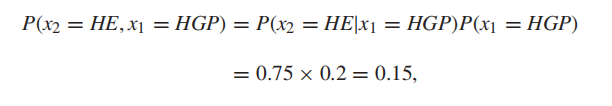
故可以得到
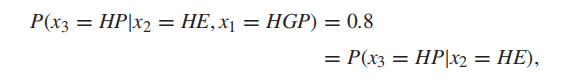
这样我们验证了基于条件概率建立的网络,这些概率编码了条件独立性,如定理2所述。






















 326
326











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








