cosx等价无穷小_等价无穷小替换注意事项

前言：之前有很多小伙伴问过我，明明我之前学的口诀是加减不可换，乘除才可换，到你这里怎么就能等价替换了呢？本篇文章用汤萌萌老师上课时举的例子来解。

受制于知识认知的程度，我写的文章也有局限性，欢迎老哥补充

正文：

1.任何一条理论都有它的局限性

各位想想当初学减法的时候，3-5不会减，你问老师怎么做，老师会说这个减不动or大概简单给你说下关于负数的事情，∵在那个年纪对于理解负数比较难。

同样的牛顿三定理局限于宏观物体在速度远低于光速时的机械运动

对于专接本考试，难度不是特别大，考试内容也相对较小，关于求极限的题型，肯定能用这条口诀来做。

2.在加减条件条件下能随意替换吗？

首先提一句话

分子与分母为同阶数(次数)时在加减运算下可进行等价无穷小替换，乘除任意替换

举个例子

这种条件下就能替换,为什么？

因为在等价替换之后的分子分母的3x,x指数都是一次，不信？用一般方法解解

用什么方法？洛，洛，洛必达天下第一！！！

可能你会认为这个是巧合，接下来会再举几个例子证明这个观点

3.例题呈上来

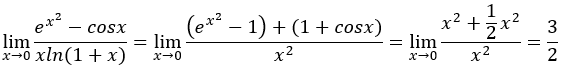
对于这道题，我们会看到等价替换之后的分子分母每一项都是二次方，∴能替换

以及值得学的+n-n小技巧

常规方法留给各位老哥们来算吧，欢迎在评论区晒出你的计算过程or私信发给我吖

4.那什么时候加减不能替换呢？能否举一个反例

我这样做对吗？答案是肯定不对

先不考虑0/0是不是等于0的问题，分子中每一项都是一次，而分母是三次方

所以不能替换，那该怎么算？

tanx-sinx，这个式子有个小技巧就是提出tanx，里面的tanx变成了1，sinx/cosx=tanx,tanx与(1-cosx)之间是乘号，所以能替换，明白了吧

明明这条结论不对，那为什么在专接本考试之前还要写

其实我觉得也对，为了防止不该犯的错误，例如第四部分开头举得错误示范

专接本考试，考高等数学就一个小时答100分的卷子，由不得你犯不该错的错误

但在考研，求极限就需要理解我今天所讲的，当然了考研求极限很难方法也很多，例如泰勒公式，以及中值定理等等知识点综合起来求极限，学到老活到老吧。

对文章有什么疑问或错误，欢迎与我一起讨论

如果觉得文章还不错，点个打赏分享再走吧

笔耕不错，有你支持