labuladong刷题笔记四（二叉树）

/* 迭代遍历数组 */
void traverse(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
    }
}
/* 递归遍历数组 */
void traverse(int[] arr, int i) {
    if (i == arr.length) {
        return;
    }
    // 前序位置
    traverse(arr, i + 1);
    // 后序位置
}
/* 迭代遍历单链表 */
void traverse(ListNode head) {
    for (ListNode p = head; p != null; p = p.next) {
    }
}
/* 递归遍历单链表 */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    // 前序位置
    traverse(head.next);
    // 后序位置
}

单链表和数组的遍历可以是迭代的，也可以是递归的，二叉树这种结构无非就是二叉链表，由于没办法简单改写成迭代形式，所以一般说二叉树的遍历框架都是指递归的形式。

只要是递归形式的遍历，都可以有前序位置和后序位置，分别在递归之前和递归之后。

所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候，那么进一步，你把代码写在不同位置，代码执行的时机也不同。

1.举个栗子

倒序打印一条单链表上所有节点的值，本质上是利用递归的堆栈帮你实现了倒序遍历的效果。

/* 递归遍历单链表，倒序打印链表元素 */
void traverse(ListNode head) {
    if (head == null) {
        return;
    }
    traverse(head.next);
    // 后序位置
    print(head.val);
}

二叉树题目的递归解法可以分两类思路，第一类是遍历一遍二叉树得出答案，第二类是通过分解问题计算出答案，这两类思路分别对应着【回溯算法核心框架】和【动态规划核心框架】。

二叉树解题的思维模式分两类：

是否可以通过遍历一遍二叉树得到答案？如果可以，用一个traverse函数配合外部变量来实现，这叫「遍历」的思维模式。
是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值，这叫「分解问题」的思维模式。

2.104. 二叉树的最大深度

（1）方法1：遍历二叉树

class Solution104 {
private:
    int depth = 0;
    int res = 0;
public:
    int maxDepth(TreeNode* root) {
        traverse(root);
        return res;
    }
    int traverse(TreeNode* root)
    {
        if (root == nullptr)
        {
            res = depth > res ? depth : res;
            return res;
        }
        depth++;   //处理该结点，++
        maxDepth(root->left);
        maxDepth(root->right);
        depth--;   //该结点处理完，回到父节点，所以--
     }
};

（2）方法2：分解问题

二叉树的最大深度可以通过子树的最大高度推导出来，这就是分解问题计算答案的思路。

    int maxDepth_method2(TreeNode* root) {
        if (root == nullptr)
        {
            return 0;
        }
        int leftdepth = maxDepth_method2(root->left);
        int rightdepth = maxDepth_method2(root->right);
        res = leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
        return res;
    }

3.543. 二叉树的直径

一旦发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

直接使用方法二分解问题实现：以每一个结点为根结点的二叉树的直径长度，等于该结点的左右子树的深度之和。

4.144. 二叉树的前序遍历

两种方法：递归、迭代

二、修改二叉树

1.226. 翻转二叉树

用「遍历」的思维模式解决：

写一个traverse函数遍历每个节点，让每个节点的左右子节点颠倒过来就行了。

用「分解问题」的思维模式解决：

对每一个结点，左子树翻转，右子树翻转，交换这两个左右子树

2.116. 填充每个节点的下一个右侧节点指针

本题完全是自己做的，采用遍历的方法。

题目的意思就是：每个结点的next指向自己最近的兄弟结点。就是这两句：

        if (node->left)
        {
            node->left->next= node->right;
            if(node->next){
                node->right->next=node->next->left;
            }
        }

3.114. 二叉树展开为链表（难）

这道题思路正确，但没写出来。labuladong说：根据思路按先后顺序写就行。

将左右子树展开，将右子树链接到左子树后面。

三、构造二叉树

二叉树的构造问题一般都是使用「分解问题」的思路：构造整棵树 = 根节点 + 构造左子树 + 构造右子树。

1.105. 从前序与中序遍历序列构造二叉树

前序遍历的第一个值preorder[0]就是根节点root的值，在中序遍历inorder里面找到root，在它之前的为左子树（长L1），之后为右子树（长L2）。preorder[1]到preorder[L1]为左子树,之后为右子树，分别递归。

2.106. 从中序与后序遍历序列构造二叉树

找出中序、后序的关系：后续遍历的最后一个结点就是根节点。

记住框架，添加边界值判断。

3.889. 根据前序和后序遍历构造二叉树

答案不止一个。但是注意：value_index只映射某一个就行。计算出左子树的长度，根据长度计算start及end的索引。

四、二叉树-序列化与反序列化

1.297. 二叉树的序列化与反序列化

（1）本题注意

树的值可以是负数；
中序遍历的方式行不通，因为无法实现反序列化方法。因为：前序遍历得到的nodes列表中，第一个元素是root节点的值；后序遍历得到的nodes列表中，最后一个元素是root节点的值。中序遍历的代码，root的值被夹在两棵子树的中间，也就是在nodes列表的中间，我们不知道确切的索引位置，所以无法找到root节点，也就无法进行反序列化。

（2）字符串分割

#include <sstream>
std::queue<std::string> Stringsplit(std::string str, const char split)
    {
        std::istringstream iss(str);	// 输入流
        std::string token;			// 接收缓冲区
        std::queue<std::string> queue;
        while (std::getline(iss, token, split))	// 以split为分隔符
        {
            if (token != "")
            {
                queue.push(token);
            }
        }
        return queue;
    }

（3）char转int

char a = ‘1’;
int ia = a - ‘0’;

五、二叉树序列化的应用

1.652. 寻找重复的子树

序列化（后序遍历）+ tree_freq_map，当freq=1时，将该结点存入结果容器中。

六、归并排序的正确理解方式及运用

1.912. 排序数组

归并排序

二叉树问题可以分为两类思路，一类是遍历一遍二叉树的思路，另一类是分解问题的思路，根据上述类比，显然归并排序利用的是分解问题的思路（分治算法）。

归并排序类似二叉树的后序遍历：

归并排序就是先把左半边数组排好序，再把右半边数组排好序，然后把两个有序数组合并。
注意合并两个有序数组的方法。

void sort(int[] nums, int lo, int hi) {
    if (lo == hi) {
        return;
    }
    int mid = (lo + hi) / 2;
    sort(nums, lo, mid);
    sort(nums, mid + 1, hi);

    /****** 后序位置 ******/
    // 此时两部分子数组已经被排好序
    // 合并两个有序数组，使 nums[lo..hi] 有序
    merge(nums, lo, mid, hi);
}
// 将有序数组 nums[lo..mid] 和有序数组 nums[mid+1..hi]
// 合并为有序数组 nums[lo..hi]
void merge(int[] nums, int lo, int mid, int hi);

2.315. 计算右侧小于当前元素的个数（难死了）

用到了归并排序。好难，最后抄的。大致理解：num最终还是排序了，所以需要存一个原始的数组，索引不可变，所以用了以下结构：

std::vector<std::pair<int, int>> value_index_vector;
for (size_t i = 0; i < nums.size(); i++)
{   
    value_index_vector.push_back(std::pair<int, int>(nums[i], i));
}

七、了解二叉搜索树性质

二叉搜索树（Binary Search Tree，后文简写 BST）的特性：

对于 BST 的每一个节点node，左子树节点的值都比node的值要小，右子树节点的值都比node的值大。
对于 BST 的每一个节点node，它的左侧子树和右侧子树都是 BST。

1.230. 二叉搜索树中第K小的元素

（1）方法一：(so easy，妈妈再也不用担心我的学习)

BST 的中序遍历结果是有序的（升序）。

（2）方法二：（优化思路）

左子树小右子树大：所以每个节点都可以通过对比自身的值判断去左子树还是右子树搜索目标值，从而避免了全树遍历，达到对数级复杂度。

想找到第k小的元素，或者说找到排名为k的元素，如果想达到对数级复杂度，关键也在于每个节点得知道他自己排第几。

比如说你让我查找排名为k的元素，当前节点知道自己排名第m，那么我可以比较m和k的大小：

1、如果m == k，显然就是找到了第k个元素，返回当前节点就行了。

2、如果k < m，那说明排名第k的元素在左子树，所以可以去左子树搜索第k个元素。

3、如果k > m，那说明排名第k的元素在右子树，所以可以去右子树搜索第k - m - 1个元素。

问题来了：如何让每一个节点知道自己的排名呢？

答：修改treenode的定义。但要维护好size值。
class TreeNode {
    int val;
    // 以该节点为根的树的节点总数
    int size;
    TreeNode left;
    TreeNode right;
}

2.538. 把二叉搜索树转换为累加树（so easy）

核心还是 BST 的中序遍历特性，只不过我们修改了递归顺序（右根左），降序遍历 BST 的元素值，从而契合题目累加树的要求。

简单总结下吧，BST 相关的问题，要么利用 BST 左小右大的特性提升算法效率，要么利用中序遍历的特性满足题目的要求，也就这么些事儿吧。

八、二叉搜索树增删查操作

1.98. 验证二叉搜索树

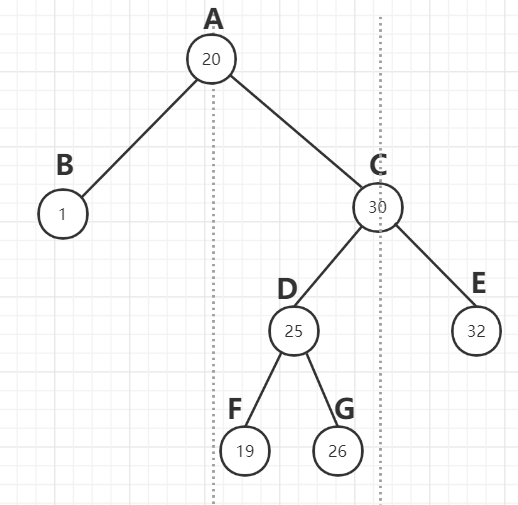
下图不是二叉搜索树，D值需要在20-30之间，F的值要在20-25之间，G的值要在25-30之间，也就是说min和max要更新。

另外需要注意的一点是：二叉搜索树的值不能相等。

2.700. 二叉搜索树中的搜索

不必全部遍历，要利用二叉搜索树的性质：左子树小右子树大。

3.701. 二叉搜索树中的插入操作

    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if (root == nullptr)
        {
            return new TreeNode(val);
         }
        if (root->val > val)       //往左子树插入
        {
            root->left=  insertIntoBST(root->left, val);
        }
        else {                //往右子树插入
            root->right=  insertIntoBST(root->right, val);
        }
        return root;
    }

4.450. 删除二叉搜索树中的节点

删除结点并保证二叉搜索树的方法很多：

我的思路：找到要删除的结点，将其右子树赋值给该节点，将左子树赋值给右子树的最后一个左子树。
labuladong：找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。

九、构建二叉搜索树

1.96. 不同的二叉搜索树（不简单）

这道题其实也是挨个遍历，以自己为根节点时，二叉搜索树个数=左子树（组合数）*右子树（组合数），如：12345，以3为根节点时，左子树的情况为2种，右子树的情况为2种，那么以3为根节点的二叉搜索树个数=2*2=4。

另外注意的一点：当lo > hi闭区间[lo, hi]肯定是个空区间，也就对应着空节点 null，虽然是空节点，但是也是一种情况，所以要返回 1 而不能返回 0。

2.95. 不同的二叉搜索树 II （难）

难搞，主要是思路。返回值 std::vector<TreeNode*>。left，right ,组合成root后也是 std::vector<TreeNode*>，返回。

十、美团面试：二叉树后续遍历

1.1373. 二叉搜索子树的最大键值和（评论区思路牛逼）

（1）注意

根结点为二叉树，求得是二叉搜索树。
二叉树最下面的叶子节点肯定是 BST
nullptr结点的值为0

（2）思路

新建一个类来存放每个结点的信息：

class NodeInfo {
public:
    bool isBST;    //是否为二叉搜索树
    int sum;       //以该节点为根节点的二叉搜索树的和 （注意是二叉搜索树）
    int min;       //以该节点为根节点的二叉树的最小值
    int max;       //以该节点为根节点的二叉树的最大值
    int maxSum;    //以该节点为根节点的二叉搜索树的最大和 （注意是二叉搜索树）
};

后序遍历

结合二叉搜索树的定义，如果【根节点的值大于右子树的最小值】或者【根节点的值大于左子树的最大值】，那么就不是二叉搜索树。

要注意的是：

当该节点不是二叉搜索树时，NodeInfo的sum就不重要了，maxSum存放的是max(leftInfo.maxSum,rightInfo.maxSum)。
而当该节点为二叉搜索树时，sum要加上该节点的值。即maxSum是【左子树maxSum】、【右子树maxSum】、【当前结点的sum】这三者之间的最大值。

十一、快速排序的正确理解方式及运用

快速排序理想情况的时间复杂度是 O(NlogN)，空间复杂度 O(logN)，极端情况下（如二叉搜索树不平衡时，所以可以用某种方式重新打乱数组顺序）的最坏时间复杂度是 O(N^2)，空间复杂度是 O(N)。

快速排序是「不稳定排序」，与之相对的，前文讲的归并排序是「稳定排序」。对于序列中的相同元素，如果排序之后它们的相对位置没有发生改变，则称该排序算法为「稳定排序」，反之则为「不稳定排序」。

如果单单排序 int 数组，那么稳定性没有什么意义。但如果排序一些结构比较复杂的数据，那么稳定性排序就有更大的优势了。

比如说你有若干订单数据，已经按照订单号排好序了，现在你想对订单的交易日期再进行排序：

如果用稳定排序算法（比如归并排序），那么这些订单不仅按照交易日期排好了序，而且相同交易日期的订单的订单号依然是有序的。
但如果你用不稳定排序算法（比如快速排序），那么虽然排序结果会按照交易日期排好序，但相同交易日期的订单的订单号会丧失有序性。