
- 前言:本文适用于有一定离散数学基础的同学总复习和没有学习过离散数学想要自学的同学参考使用
- 数理逻辑
永远赋值为真的式子为重言式
永远赋值为假的式子为矛盾式
至少有一个式子使其为真的时候为可满足式
文字:命题变项及其否定的总称
简单析取式:由有限个文字析取组成的
简单合取式:由有限个文字合取组成的
析取范式:有限个合取式析取而成
合取范式:有限个析取式合取而成
每个变元都出现一次的简单合取式都为极小项
每个变元都出现一次的简单析取式都为极大项
主析取范式:极小项的析取
主合取范式:极大项的合取
常用化极小项,极大项的方法
例如有三个命题变项:
若要把
利用分配律
若要把
- 方法1
- 方法2
观察这个公式为主合取范式,我们通过插缝观察得
与非
用与非可以表示所有的运算符
或非表示所有的运算符
证明方法
- 直接证明
- 附加前提证明
- 归谬法
结论为蕴含式的时候用附加前提证明
归谬法假设结论不成立,推理出和题目条件有矛盾的地方
- 一阶逻辑(谓词逻辑)
量词(全称量词
谓词
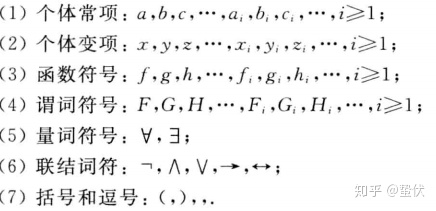
一阶逻辑式通过代换利用基本的等值式
分配等值式
Correct
量词辖域收缩与扩张等值式
易错:
例:
则
闭式:
给函数变项符号和谓词变项符号“赋值”就是解释
任何解释的任何赋值下为真:永真式
任何解释的任何赋值下为假:矛盾式
实例代换
利用
然后判断
求前束范式方法
前束范式是将变元放到最前面(常用换名规则)量词前面不能有非
辖域不同要用换名规则
例:求此式的前束范式
换名规则
求前束范式的关键就是要记住量词辖域收缩与扩张等值式,以及注意易错点
- 集合论
空集是
三个符号的区分
“属于”是指元素和集合的关系
例:
"真包含
但若
全部自己的个数为
幂集
把
例:
先写出
则
集合的基本运算
交
分别定义
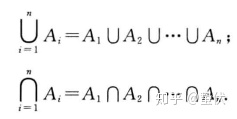
绝对补
设
对称差
证明一般用定义证明或利用恒等变换
集合的计数
- 二元关系和函数( 重点)
笛卡尔积
笛卡尔积与运算关系的证明利用定义证明
二元关系
全域关系
恒等关系
关系矩阵
设
关系的运算
定义域
值域
域
特殊关系
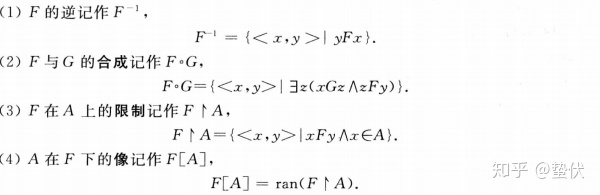
(1)
(2)
进而有归纳法得
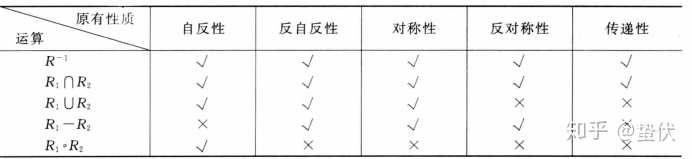
重重点,关系的性质(下图中
以下5种性质一定要掌握( )
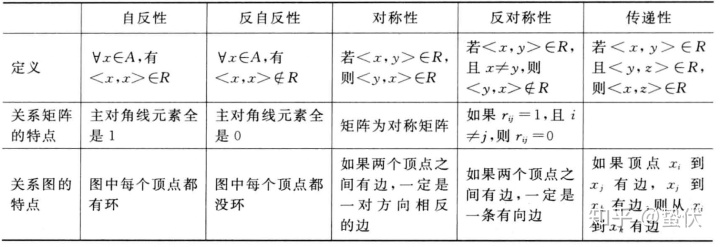
若要证明上面的任意的性质,需要严格按照定义来看
常见关系的性质的延申
关系的闭包
集合
自反闭包(
对称闭包(
传递闭包(
矩阵
自反闭包(
对称闭包(
传递闭包(
图
自反闭包( 哪一个节点没有环就加上环)
对称闭包( 单向边改为双向边)
传递闭包( 使其连通)
等价关系和偏序关系
- 等价关系(
)
是自反的,对称的,传递的
等价类:满足等价关系的元素的集合,简记
商集,等价类组成的集合,简记
划分
称
- 偏序关系(
)
是自反的,反对称的,传递的
记作
下面有几个定义需要大家注意


这个地方主要就是要区分最小元和极小元,最大元和极大元的区别
下面我们来看一个图形
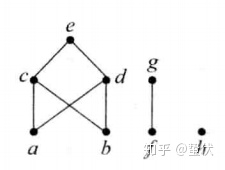
此时我们依照这个哈斯图可以写出其对应的偏序关系
其极小元为:
极大元为:
无最小元,无最大元
无上界,无下界
无上确界,无下确界
函数
定义:设
相关概率及其结论
- 函数相等
条件
-
-
均有
-
-
为函数(
)
- 则称
为
到
的函数,记作
- 有集合
(
上
)(所有以
为定义域
为值域函数关系的集合)
- 则称
- 函数的像
- 则
在
下的像:
的函数的像
- 则
- 函数的分类
- 满射:
- 单射:唯一的
对应唯一的
- 双射:即使单射也是满射
- 满射:
- 掌握构造单射,满射,双射的条件
- 函数复合相关定理
-
-
都是满射/单射/双射则
也是满射/单射/双射
- 证明满射定义,证明单射假设
-
- 反函数
- 单射函数一定有反函数,且其反函数使双射函数
- 图
有关图的相关概念
有几个顶点(Vertex)就称为几阶
零图:没有边即(Edge=空集)
平凡图:一阶零图
简单图:没有平行边和环
匹配的相关概念:
匹配(边独立集): 任2条边均不相邻的边子集
极大匹配: 添加任一条边后都不再是匹配的匹配
最大匹配: 边数最多的匹配
匹配数: 最大匹配中的边数
设
图的同构:两个图展开以后长一个样
判断条件:1.边数相同,顶点数相同
2.度序列相同 d(v1),d(v2)….
3.顶点关联的顶点数相同
完全图:每一个顶点都相邻 记作Kn
子图:子图的顶点属于原图的顶点
子图的边属于原图的边
顶点集:由原图所有顶点组成的图,没有边
导出子图:顶点集V' 和 两个顶点都在V'中的边构成的图
生成子图:包含原图的所有顶点,边不一定
简单通路:每个边只经过一次的通路
初级通路:每个顶点只经过一次的通路
连通分支:有连通关系构成的导出子图
(连通分支数的个数记作P(G))
G-v 从G中删除V这个节点和其关联的边
点割集 :删除这个点之后图就感觉被切断了一样(最小的切断)
G-e : 从G中删除e这条边
边割集:删除这个边之后图就被切断了(最小的切断)
平面图中面的相关概念
G的面: 由G的边将平面划分成的每一个区域
无限面(外部面): 面积无限的面, 用
有限面(内部面): 面积有限的面, 用
面
最短路径Dijkstra算法
树的相关概念
有向树: 基图为无向树的有向图
根树: 有一个顶点入度为0, 其余的入度均为1的
非平凡的有向树
树根: 有向树中入度为0的顶点
树叶: 有向树中入度为1, 出度为0的顶点
内点: 有向树中入度为1, 出度大于0的顶点
分支点: 树根与内点的总称
顶点
树高: 有向树中顶点的最大层数
图的相关结论希望记住可以帮助解题
握手定理:
任意无向图和有向图的所有顶点度数之和都等于边数的2倍, 并且有向图的所有顶点入度之和等于出度之和等于边数
对于任意的图,奇数度数的顶点的个数一定是偶数
完全图相关结论:
总边数:
总度数为
总边数:
二部图相关结论:
判断是否为二部图
无向图
欧拉图相关结论:
判断欧拉图
无向图
有向图
哈密顿图相关结论:
判断哈密顿图
定理1

定理2
设
则为哈密顿图
定理3
设
定理4
设
定理5
当
定理6
在
平面图相关结论:
设
平行边和环不影响平面性
平面图各面的次数之和等于边数的2倍(
若
极大平面图:若
极小非平面图:若
欧拉公式:
推广:一个连通的平面图
同胚:一个图的边上插入一些新的顶点而得到的图
定理1:一个图是平面图当且仅当其不包含同胚于
设
(
怎么画对偶图
每条边必须经过一次
树的相关结论:
Huffman算法
最佳前缀码(利用以上算法)左0右1
行变2叉树
中序行遍法: 左子树、根、右子树(左,根,右)
前序行遍法: 根、左子树、右子树(根,左,右)
后序行遍法: 左子树、右子树、根(左,右,根)
波兰符号法:按前序行遍法访问表示算式的2叉有序树, 并舍去所有括号
逆波兰符号法(后缀符号法): 按后序行遍法访问表示算式的2叉有序树, 并舍去所有括号
完完完完完完完完完完




















 3642
3642











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








