python gmm em算法 2维数据_一文说懂EM算法及其在HMM和GMM中的应用

一、EM算法要解决的问题

EM算法就是最大期望算法，用于解决无法观测隐性变量的概率模型求参数的问题。这句话是什么意思呢？举个例子，如果一个学校只有男生，假设男生身高符合正态分布，此时需要根据统计得到的男生身高计算出正态分布模型中的均值和方差，那么我们可以直接计算。但是如果学校既有男生也有女生，而且因为统计时的疏漏，无法区分统计的身高是男生还是女生的身高，此时要计算模型参数，就需要EM算法了。

EM算法依旧通过最大似然估计法来计算概率模型的参数。如果我们知道在状态z下导致事件y发生的概率，那么我们在计算事件的最大概率时，可以把表达式写为：

然后令其求导=0的方式求出

，也就是求事件发生的概率最大时的参数。但是如果有多个状态都可能导致事件y，而我们没法确定到底每一件状态导致了事件y，那么我们该如何计算这个参数使得事情发生的概率最大呢？我们可以将表达式写成：

之所以是求和符号，就是因为希望通过求Y的边缘函数表示其概率。

二、EM算法的E步是怎么得出的？

我们在使用EM算法计算时，常规步骤通常为E步设立公式，然后M步求导，得到参数值再代入E步的公式，如此反复计算。可是我们E步中的公式是怎么来的呢？下面就进行解释

因为不知道

，我们没有办法直接求得

。但是我们发现

是单调递增的，而且有上限（因为概率在0到1之间），那么就可以得知

会收敛到某一个值，那么就意味虽然不能求出最优解，但是我们可以先随意初始化一个

，然后通过不断优化

使得

不断的变大，最终达到收敛状态，得到其下界以及这个下界对应的参数

。既然如此，那么就应该满足

。我们来看它们的差值：

由于log中带有求和函数，使得式子难以处理，所以我们利用琴生不等式来对前半部分缩放。所谓琴生不等式就是：

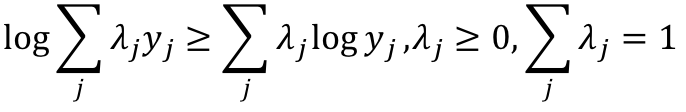
经过不等式变换可得：

注意后半部分之所以可以加上

，是因为它的和为1，而且

是一个常数。我们将公式稍作变形：

虽然我们无法直接求

，但是可以不断的增大

来逼近

。如果我们将

取值为上一次迭代的值

，那么：

逼近的效果如下图所示:

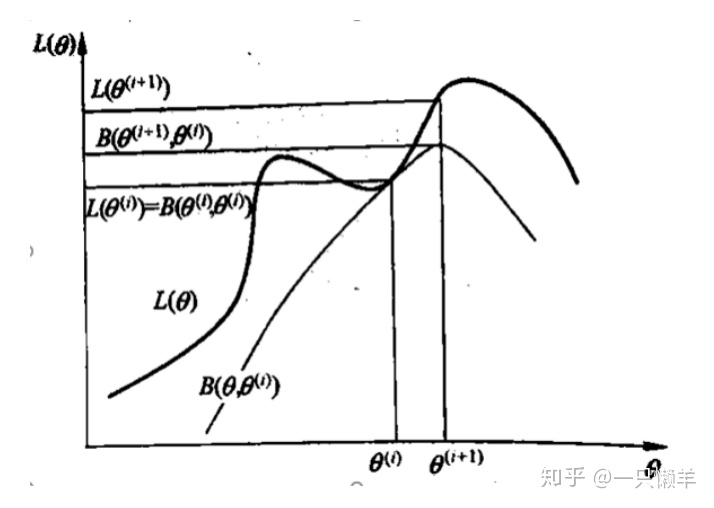
也就是说，我们要求一个参数，使得B最大，最接近原来的概率，即

在这个过程中，我们去掉常量，发现要想求得最大概率，最终只和在上一个参数

背景下的概率分布（即已知事件y发生，判断z是哪种隐状态的概率）和现有的事件发生的概率有关。

这就是为什么我们使用EM算法，一开始计算期望时就用

来计算的原因！而我们回头看，整个公式最为关键的地方就是为前半部分式子添加了

，为下面的合并两项奠定了基础。

三、EM算法在求解HMM和GMM中的求解

3.1 EM算法在抛硬币模型中的参数求解过程

问题背景是如果有三枚硬币abc，他们出现正面的概率分别为π，p，q，我们先抛掷a硬币，如果是正面，则用b抛掷，如果是反面，则用c抛掷，然后记录下b或者c抛出来的结果。现在得到观测结果为1、1、0、1、0、0、1、0、1、1。问如何估计三个硬币正面出现的概率，即三硬币模型的参数。

注意每一次的抛掷结果是独立的，所以事件的总概率是各个事件的连乘。由于我们要求的完全数据对数似然函数明确，因此我们直接进入到E步，得到事情最大概率的表达式：

我们仅看B这一项，将其分解成两部分，第一部分是第一项，第二部分是2到N项，计算可得：

我们发现D中的项也可以分解为N-1项形式如C的式子，因此我们只考虑C即可。Z代表的是选择哪一枚硬币，我们考虑其中一枚硬币，其中每一个硬币又都有两种状态，就是正面和反面。

其实第二步最为关键，因为将累乘符号分解以后，（2）中的F和G有关，而E则和G无关，又因为E是指硬币z在不同取值下的概率，其实等于1，这样n-1个1累乘法依然是1，所以最终得到（6）这一表达式。

我们知道

可以分解成C+D，而每一个C都会得到类似（6）中的表达式，那么

的表达式可以表示成：

我们回过头来梳理一下思路，看看这些符号都代表什么意思，z表示隐状态，也就是硬币A抛出来的结果，是未知的，而y表示最终看到的观测结果。

最后进行M步，在上面我们可以用π、p、q表示

和

，也就是π、p、q和这两个概率值的关系式。通过对π、p、q初始化一个比较合理的值，计算出第一个事件中的这两个概率，表达式如下：

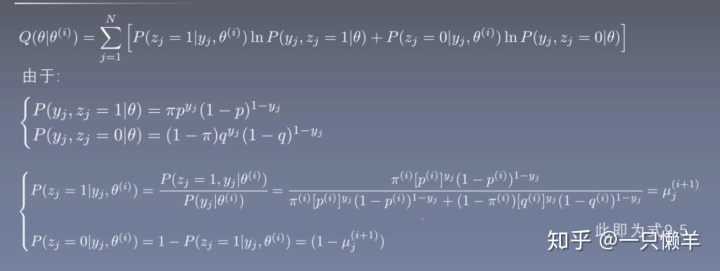
然后分别对π、p、q求导，比如对π的求导公式为：

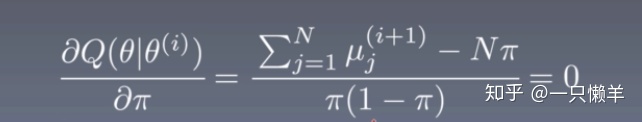
利用刚才算得的

，计算π、p、q。然后再计算下一个事件中的

，不断迭代，使得π、p、q的值不断收敛。

3.2 EM算法在GMM模型中的参数求解过程

GMM模型就是高斯混合模型，具有如下形式的概率分布：

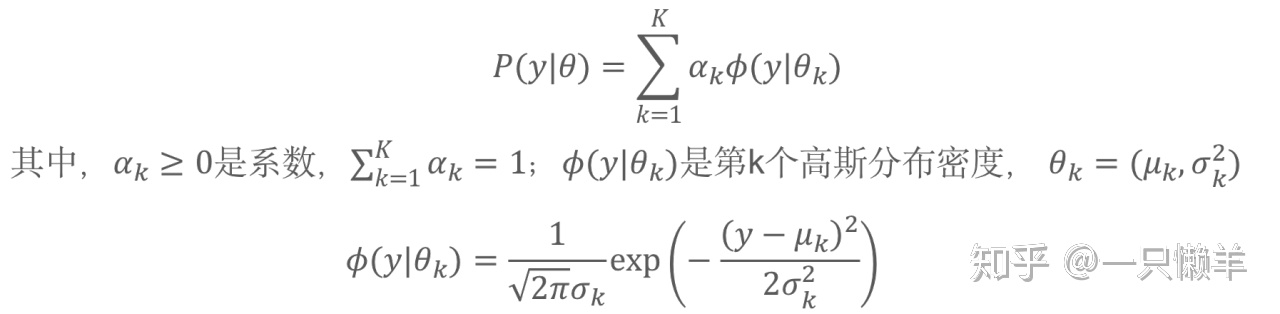
用文章开头男女生身高的例子来理解，假设观测数据y_j,j=1,2,…,N是这么生成的：依据概率

选择使用男生还是女生的高斯分布模型，即选择第k个高斯分布模型ϕ(y|θ_k)，然后使用第k个分模型的概率分布生成观测数据y_j。

第一步，确定隐变量和完全数据的对数似然函数。对于观测数据y_j，定义k个隐变量：

在这里，之所以要将隐变量定义成这种形式，是为了统一使用

这种指数形式来表达在第j次观测中（或者说事件）由第k个模型生成的概率，否则就要把每一个事件的生成概率写出来，然后再乘起来，这会显得很累赘，而且不方便对公式进行变形。

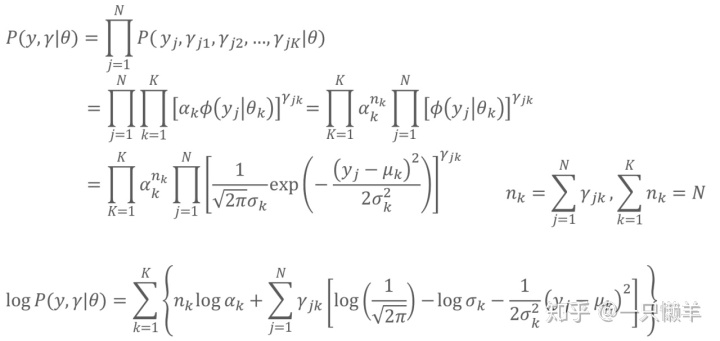
第二步，套用EM算法的E步，可得：

。代入上面公式可得：

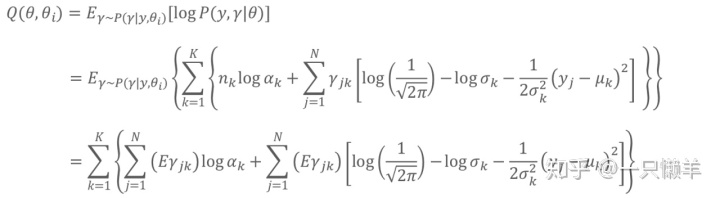
因为

取值为1或者0，那么

只需要处理

取值为1的情况，而无需处理

为0的情况，因此：

接下来计算M步，通过分别对

求导，令其等于0，可以得到下面的式子，其中响应度的计算可以通过对参数的取初始值得到，再将计算结果代入下式：

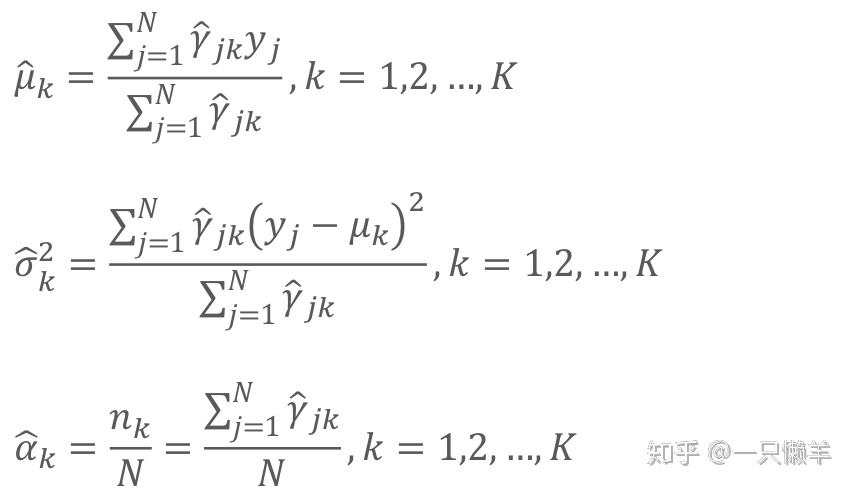
然后利用

重新计算得到响应度

，反复迭代。

3.3 EM算法在HMM模型中对概率学习问题的应用

我们知道HMM模型需要解决三个问题，分别是概率计算问题、概率学习问题和状态预测问题。EM算法解决的就是无监督的概率学习问题，学习问题是指已知观测序列，估计模型

(π、A、B)的参数，使得模型观测序列概率

最大。

老规矩，先确定完全数据的对数似然函数，观测数据

，隐变量

，完全数据

，完全数据的对数似然函数是

接下来设立E步函数：

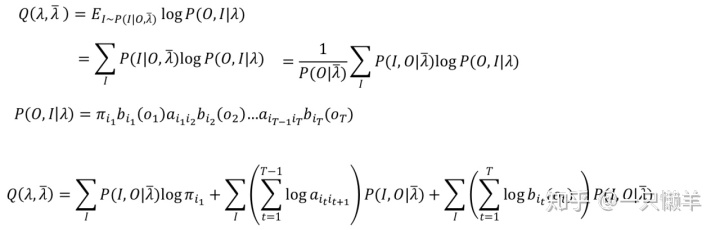
最后M步极大化Q函数：

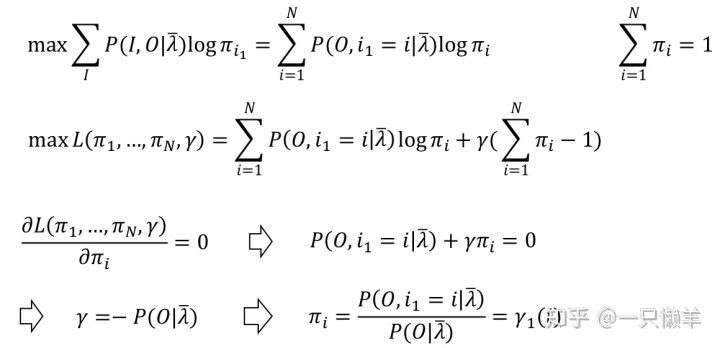
同理可以对矩阵A和矩阵B中的每一项求解，得到：

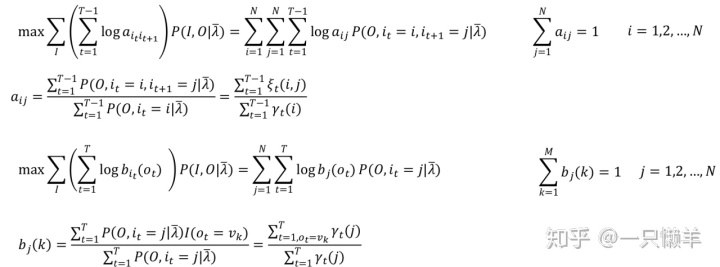
通过这几个例子，我想应该能理解算法是如何辅助模型来求解的。计算过程确实非常复杂，一度让我感到奔溃，再加上这么多的公式输入，也很损耗耐心。但是不深入具体过程，就没法理解EM算法是如何起作用的，又适用于什么场景。

耐心、耐心再耐心！

耐心拯救小羊！希望也能对你有所帮助。