数学作图工具_数学趣览X 曾让古希腊人犯怵的三大几何作图难题

最新推荐文章于 2021-06-20 17:57:13 发布

weixin_39843986

最新推荐文章于 2021-06-20 17:57:13 发布

阅读量436

点赞数

文章标签：数学作图工具

本文链接：https://blog.csdn.net/weixin_39843986/article/details/111389493

版权

点击蓝字 关注我们

古代希腊人较重视直尺和圆规作图，以在数学中训练人的逻辑思维能力，发展其智力。因此，他们较大的限制了直尺和圆规这两种作图工具的使用：①作图时，只能有限次使用直尺和圆规；②不能利用直尺上的刻度或其他记号；③不能把直尺和圆规合并使用，也不能把几个直尺合并使用。在这种限制下，即便一些简单的几何作图也无法解决。最著名的是被称为几何三大难题的三个古希腊作图难题，即三等分任意角问题、立方倍积问题和化圆为方问题。

当时很多有名的希腊数学家，都曾着力研究过这三大难题，但由于尺规作图的限制都一直未能如愿。两千年来几十代人为之绞尽脑汁，均以失败告终。直到19世纪90年代，人们证明了这三个问题不可能用“尺规作图”来解决，这才结束了历时两千年的数学难题公案。因此，现今的中学生们不必再去搞什么“几何三大难题”，避免再去步前人失败的后尘。值得一提的是，如果允许借助其他工具或曲线，这“三大难题”都可以解决，也就不成其为“难题”了。

1. 三大几何难题的由来

(1)三等分任意角问题。就是仅用直尺和圆规将任意角三等分。一条线段，可以很容易地将其三等分。不仅三等分，而且可以任意等分。借助数学联想很容易把这种想法移植到角上，即将角三等分。这是历史上最为长久、流传最为广泛、耗费人的精力最多的一道几何作图题。

(2)立方倍积问题。就是要求作一个立方体，使其体积等于已知立方体体积的两倍。关于立方倍积问题的产生，有这样一个传说：公元前400多年，古希腊德里斯群岛上流行着瘟疫，死亡阴影笼罩着人们。人们对瘟疫束手无策，于是就到神庙去祈求太阳神阿波罗的保护。阿波罗的代言人——神殿的女司祭毕菲亚对大家说，这次瘟疫是神认为您们对神不够虔诚的惩罚。神殿里的正方体祭坛太小了，要使它仍保持正方体，但体积应为原来的两倍，这样神就可免除您们的灾难。于是“立方倍积”问题便流传开了。

(3)化圆成方问题。求作一个正方形，使它的面积等于已知圆的面积。从数学思想最基本的逻辑学观点来看，这个问题的产生似乎是必然的。如果您得到一个圆规，画出的第一个图形就是圆。另外，还有一个十分自然的图形——正方形。其中每一个图形都有一个确定的面积。在这两个具有相同面积的图形之间，可以自然地搭起一座桥来，就是其中的一个图形变换成另一个图形。因为变换只能用圆规和直尺，所以就可能产生这样个问题：利用圆规和直尺作出一个面积等于已知圆面积的正方形的一条边。这就是“化圆成方”问题。

2. 三大几何作图问题为什么不能用尺规作出

在平面几何作图题里，总可以把一条已知线段(或给定的某一线段)当作“单位长线段”，即可把已知线段作为长度为1的线段。于是利用尺规作图，很容易将该线段n等分，从而求得1/n的线段，再将此线段m倍，又可得m/n的线段。于是一切以有理数为长度的线段都可以作出来。

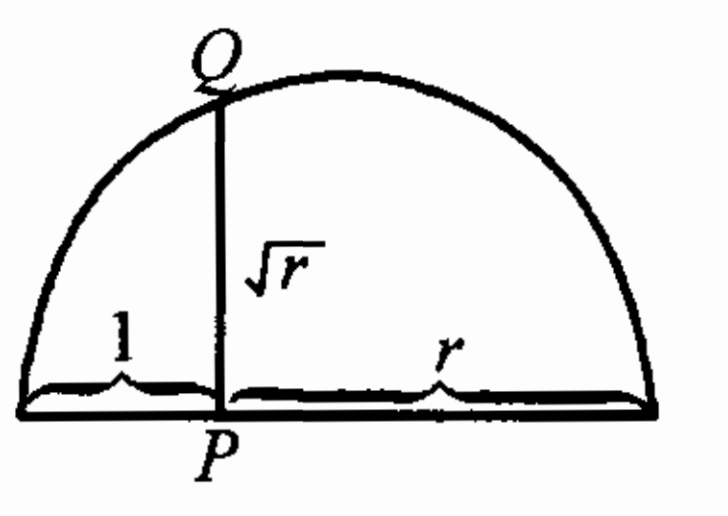
设r为任一正有理数，则以平方根长度的线段也可以作出来。事实上如图1所示，利用1+r为直径作半圆，从线段连接点P引垂线交半圆周于Q，则

。由此可知，一切以正有理数的平方根为长度的线段都可用尺规作出来。

反复利用上述方法，又可将

为长度的线段作出来。一般说来，只要是由有理数经过有限多次“加、减、乘(乘方)、除、开平方”五则运算得出的数量，都可以用尺规作出以这些数量为长度的线段来，我们把这些数量叫作“可作图几何量”。例如下面的数量：

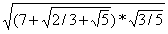
就是一个“可作图几何量”。因此，要判断一个平面几何上的图形是否用尺规可作，只要分析一下所要确定的几何量是否为“可作图几何量”就行了。

现在我们回到三大几何作图难题上来

(1)三等分任意角问题：设已知角的三分之一为a，则已角为3a，取它的余弦，由三倍角余弦公式得cos3a=4cos3a-3cosa，即8cos3a-6cosa-2cos3a=0，令2cos3a=m，2cosa=x，则可得到：x3-3x-m=0，这就是三等分任意角的代数方程。如果这个方程的根x可用尺规作图作出来，则角的大小也可用尺规作出来，然而这个方程的根不能表示成“可作图几何量”。因此，三等分任意角问题不可能用尺规作图作出。

(2)立方倍积问题：设正方体祭坛的棱长为a，新立方体祭坛的棱长x，则有x3=2a3，不妨设a=1，于是

。而

不是“+、-、x、÷、√”五种运算所能得出的。所以它是一个“非几何作图量”。

3. 不用尺规作图时“三大几何难题”的可能性

(1)三等分任意角问题：如图2所示，设所要三等分角为∠AOB，取一直尺，其一端点为P，另在尺边缘上取一点Q，以O为圆心，OQ为半径作半圆交∠AOB的两边于A、B。P点在OA的反向延长线上移动，Q点在半圆上移动。当直尺刚好通过B点时，画出直线PQB，这时不难证得∠APB=1/3∠AOB(证略)。

(2)立方倍积问题：如图3所示，作互相垂直且交于O的两条直线m和n，分别在其上取OA=a,OB=2a。取两个其边互相垂直的L型曲尺，使一个曲尺的顶点在n上，过A点；另一曲尺的一边过B点，顶点在m上，且两曲尺的一边互相密合。这样两曲尺的顶点分别在m, n上确定了C、D两点，OC即所求正方体棱长x。

化圆成方问题：如图4所示，设已知圆半径为r，则它的面积为πr2。我们用木料作一正圆柱体，使其下底与已知圆等积，高为r/2。然后，把这圆柱在平面上滚一周，在平面上就滚出了一个矩形。它的长为2πr，宽为r/2，则这个矩形面积为2πr*r/2=πr2，与圆面积是相等的。这样问题就变为求作一个正方形与此矩形具有相等的面积，这显然是容易办到的。