二元偏导数存在的条件_偏导连续、偏导存在、连续、可微，之间的关系

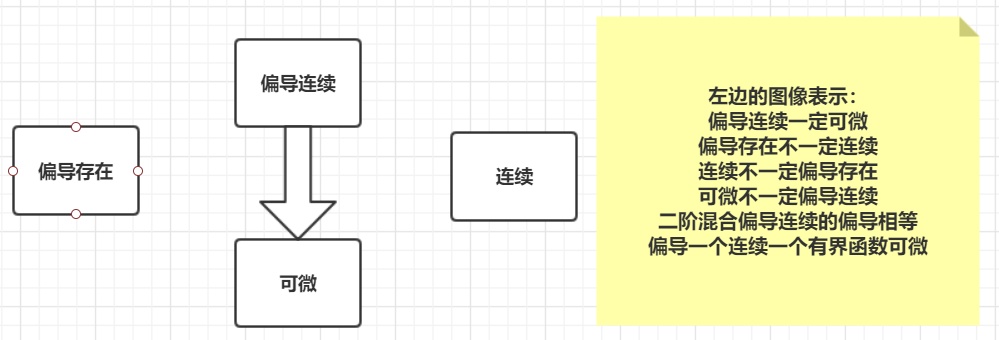
在多元函数的领域里面，主要就是偏导的关系，所以我就为大家梳理了这些。同样那些定义定理我也不做证明，主要是说明一些不一定的反例。

同样在解释它们的关系之前我先说说这几个的定义。

偏导连续：先用定义求出该点的偏导数值c，再用求导公式求出不在该点时的偏导数

，最后求

当(x,y)趋于该点时的极限，如果

，即偏导数连续，否则不连续。

x方向的偏导.

设有二元函数 z=f(x,y) ，点

是其定义域D 内一点。把 y 固定在

而让 x 在

有增量 △x ，相应地函数 z=f(x,y) 有增量（称为对 x 的偏增量）

关于y方向的偏导我就不写了。

偏导存在：若二元函数在区域D上可微，则f在每个自变量的偏导都存在。

连续：设f为定义在点集

上的二元函数，

,

只要

就有

可微：（有图我就不打了，太浪费时间）

---

偏导存在不一定连续

连续不一定偏导存在

可微不一定偏导连续

最后再给大家补充几道题目方便大家理解熟悉。

参考资料： 数学分析学习指导书·下册 、华师大数学分析下册、数学分析中的反例