hertz接触理论_圆柱滚子轴承接触分析方法对比

宁诗哲 屈福政 张春光

0 引言
止推圆柱滚动轴承因其承载能力强的特点，在旋转类机械中得到了广泛应用，而其承载能力、变形与刚度等问题又与轴承的受力状态密切相关，因此, 轴承受力分析成为轴承研究的基础[1]，尤其是接触情况、接触半宽、弹性趋近量等参数是研究并设计滚动轴承的关键。                      早在100 多年前，Hertz 即对点接触和线接触的弹性接触问题给出了理论解[2]。20 世纪60 年代后，随着计算机的普及，出现了更多的研究方法。Harris[3] 曾采用切片法对载荷作用下接触应力的分布进行研究。王大力等[4] 采用有限元法对球轴承接触问题进行分析。本文对现有几种计算圆柱滚子轴承分析接触情况的方法进行描述，并通过实例计算，得到不同方法的各自优缺点及适用范围。

1 接触应力计算方法
1.1 Hertz 接触理论
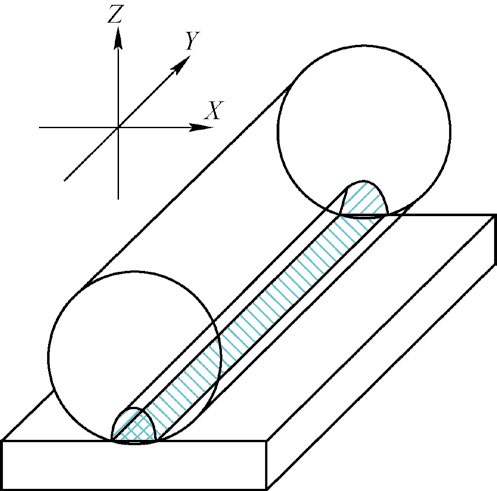
对于弹性体的接触问题令人满意的分析，最早是由Hertz 得到的。分析中Hertz 采用了如下假设：1）接触物体只产生弹性变形，并服从虎克定律；2）负载垂直于接触表面，即不计及接触物体之间的摩擦力；3）接触面的尺寸与接触物体表面相比很小。通过分析得到了线接触下的接触半宽和最大接触应力的公式，而且接触应力在接触半宽上呈椭圆形分布，见图1。

图 1 Hertz 接触模型示意图

式中：a Ω 为接触半宽， F 为轴向载荷， lt 为有效接触长度， R 为滚动体半径，E ＇为材料参数，v 1、E 1 为滚动体的泊松比和弹性模量， v 2、E 2 为支撑架的泊松比和弹性模量。            在满足Hertz 接触的假定下，计算出接触半宽和最大接触应力。随着载荷的增大、接触长度的减小，接触半宽和最大接触应力都会增大。而滚动体的半径越大，接触半宽越大，最大接触应力越小。

1.2 基于弹性力学和影响系数法的数值计算方法
根据弹性力学可以得到滚动体与滚道之间的力平衡方程和变形协调方程。式（1）可以很好地表达接触模型，但在应用到滚动轴承情况时，该式并没有解析解。因此，要用数值方法进行求解。目前关于滚动体接触计算方法包括切片法和影响系数法，相比于切片法，影响系数法考虑了接触边缘效应的影响，因此，更接近实际的接触情况&#x