阶跃函数卷积自己_详细推导卷积算法

本文的主要思路如下：

1 从测量飞船的例子开始

假设

表示第

时刻测量到的宇宙飞船位置。由于信号存在干扰，我们取该时刻的前

次测量结果的期望作为该次测量的最终结果。我们用

表示这

次测量里的一个时刻，我们假设

时刻对应的权重为

，则

越接近

，它应越重要。这里所有的值都是标量。求

时刻前

次测量的期望

则，期望求解如下：

当

：

上面的积分运算过程被定义为卷积运算，标记为

，其中

对应卷积核（概率密度函数），

对应输入。

在计算机科学中离散卷积更符合实际情况，即上诉第一个公式，此时

对应概率质量函数。

直观理解：卷积运算表示前

次输入的加权平均，这里的

表示关注范围

2 卷积运算

2.1 卷积核翻转

飞船的例子描述的是1D的情况，如果扩展到2D，考虑采用2D卷积核，那么：

其中：

• ：输入的2D数据，例如一张灰度图片
• ：2D卷积核，如果卷积核下标超出卷积核范围那么设置为得到的值恒为0

假设

，即：

那么：

从结果上看，卷积操作为：卷积核分别沿着45°、135°轴翻转180°，然后沿着输入的左上角依次滑动，每移动一次，计算一次加权平均值。

翻转卷积核之后的过程如下：

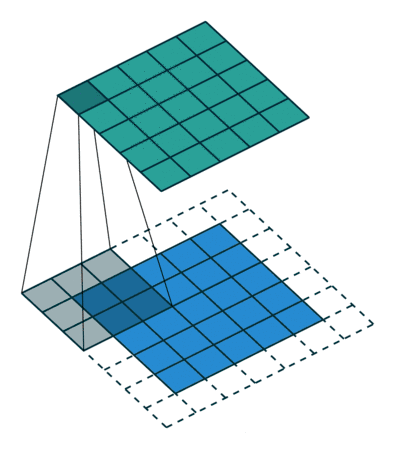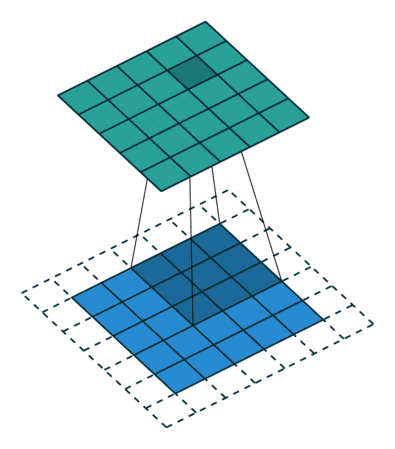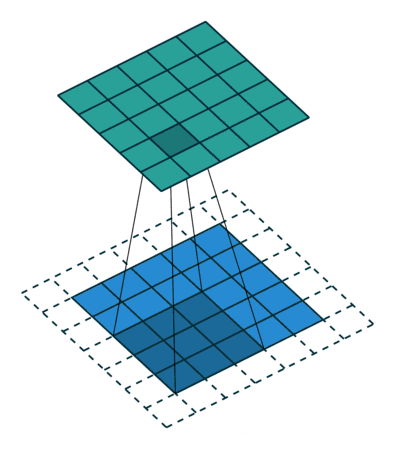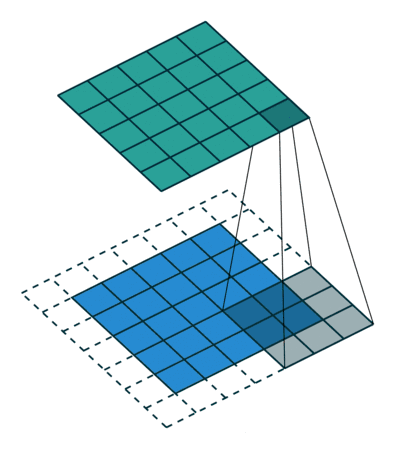
2.2 卷积核不翻转

上述卷积操作需要对卷积核进行翻转再运算，这样的操作满足卷积运算的交换律。但是在神经网络中，交换律不是很重要的性质。通常神经网络库会实现一个互相关函数，和卷积运算几乎一样，除了没有对卷积核翻转。

通过互相关函数，卷积核在滑动操作时不需要翻转。现在主流框架实现的方法都是上述互相关函数。后面值的卷积也都是互相关函数

2.3 卷积运算的特点

1. 稀疏交互

如图2.3.1 所示，卷积操作中，一个输入单元只和部分输入单元发生交互，一个输出单元也之和部分输出单元发生交互；而如图2.3.2所示，全连接操作中，每个输入单元都和所有输出单元发生交互

图2.3.1 卷积操作

图2.3.2 全连接操作

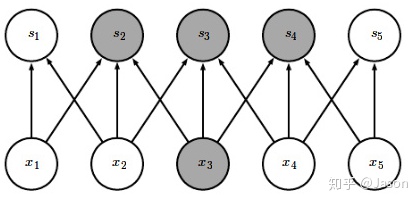
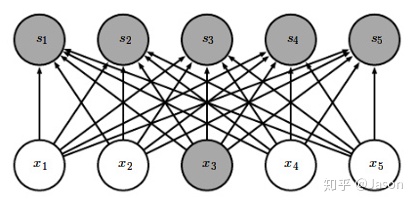
2. 参数共享

卷积运算中多个运算使用相同的参数（同一个卷积核）。而全连接中每个运算都使用自己的参数，每个参数都只使用一次

3. 等变表示

假设有平移函数

（例如：

）、卷积函数

、卷积结果

。根据卷积公式，卷积操作满足

，即：

如果输入数据向某个方向平移多少个单位，卷积操作输出数据同样向同一个方向移动同样的单位长度

图2.3.3 平移等变，卷积操作向右（蓝->红）减小输入，输出同样向右减小输出

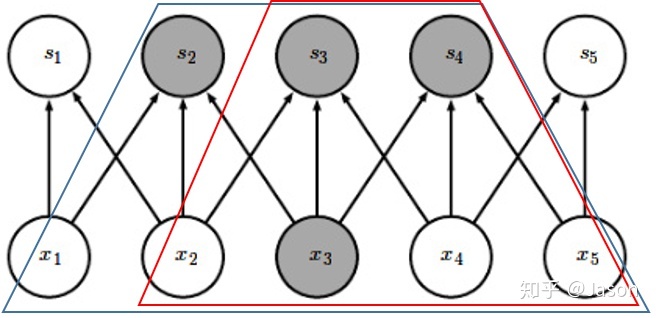
3 卷积的变体

3.1 多通道卷积

针对多通道输入以及多通道输出，卷积操作变体如下：

其中：

• ：第
  通道的
  行
  列的输出值
• ：第
  通道的
  行
  列的输入值
• ：第
  个卷积核的第
  通道的
  行
  列的输入值

3.2 调整卷积步幅

调整步幅，假设stride=s，那么卷积公式变体如下：

3.3 原始图象不同填充方法

1. valid卷积：卷积核只允许访问V中能够完整包含卷积核的位置，这种操作会缩小输出尺寸，缩小大小为
   ，例如卷积核为3x3，那么长宽分别缩小2，2
2. same卷积：为了保证输出尺寸不变，输入的图像先用0填充，保证输出的shape和输入的实际shape一样
3. full卷积：上面的操作都会导致边缘像素被访问的次数变少，也就相当于忽略了弱化了边缘像素的作用，所以full卷积就是保证每个像素被访问次数都是一致的。所以输出图像的宽度=m+k-1

4 卷积求导

结合以上几种卷积变体，卷积前向通用公式如下：

在反向传播过程中会得到该输出的误差为：

4.1 针对卷积核求导

为了更好理解，这里假设输入输出通道数=1，stride=1，所以：

所以，上述也是卷积操作，输入

，卷积核

，过程类似下图：

图4.1.1 误差为输入，前向输入为卷积核的卷积操作示意图

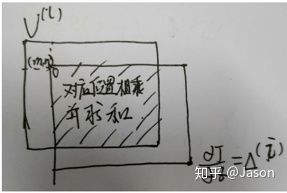
4.2 针对输入求导

为了更好理解，这里假设输入输出通道数=1，stride=1，所以：

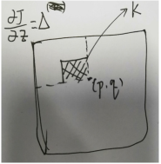
同样也属于卷积操作，上述过程类似下图：

图4.2.1 以误差为输入，翻转后的卷积核为卷积核的卷积操作