中心极限与大数定理律的关系_大数定理的通俗理解（辛钦、伯努利、切比雪夫大数定理）...

大数定理简单来说，指得是某个随机事件在单次试验中可能发生也可能不发生，但在大量重复实验中往往呈现出明显的规律性，即该随机事件发生的频率会向某个常数值收敛，该常数值即为该事件发生的概率。

另一种表达方式为当样本数据无限大时，样本均值趋于总体均值。

因为现实生活中，我们无法进行无穷多次试验，也很难估计出总体的参数。

大数定律告诉我们能用频率近似代替概率；能用样本均值近似代替总体均值。

很好得解决了现实问题。

大数定理严格的数学定义分为两种，一是弱大数定理：

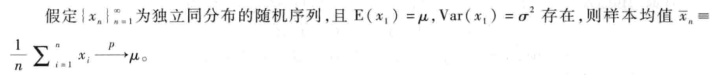
即样本均值会随着n的不断增大，依概率收敛（简称i.p.收敛 converge in probability,）到真正的总体平均值。

那么什么叫依概率收敛呢？其定义如下：

意思是，当n越来越大时，随机变量x落在

外的概率趋近于0，还是有可能落在外面的，只不过可能是很小，且会随着n的增大，这种可能越来越小。

二是强大数定理：

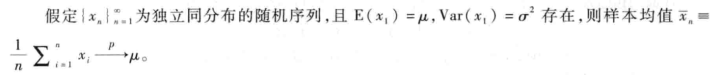
我们仍可这样定义，只不过这里不再是依概率收敛，而是几乎必然收敛(简称a.s.收敛converge almost surely)，可以理解为此时p=1，以确定的为1的概率收敛，即没有x会落在

外面，就算有，这些点在测度下也是可以“忽略”的。

也就是说明，二者的条件其实是一样的：即iid和期望存在（好像也有证明不需要iid的？这里先不深挖了，看到再补）。但是结论不同，弱大数定律证明了：随着n的增大，平均值接近真实期望值的可能性也在增大。强大数定律证明：随着n的增大，平均值基本上就接近真实期望值了。

大数定律有这么几个版本

1、伯努利大数定理：从定义概率的角度，揭示了概率与频率的关系，当N很大的时候，事件A发生的概率等于A发生的频率。

设fn为n重伯努利实验中事件A发生的次数，p为A在每次实验中发生的概率，则对任意给定的实数ε>0，有

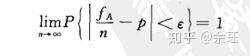
即n趋向于无穷大时，事件A在n重伯努利事件中发生的频率fn/n无限接近于事件A在一次实验中发生的概率p。

2、辛钦大数定理：揭示了算术平均值和数学期望的关系

设X1,X2,⋯是独立同分布（iid）的随机变量序列，且它们的期望值存在，记为E(Xi)=μ（同分布隐含条件即为期望相同），则对于任意的ɛ>0，有

辛钦大数定律从理论上指出：用算术平均值来近似实际真值是合理的。

当Xi为服从0-1分布的随机变量时，辛钦大数定律就是伯努利大数定律，故伯努利大数定律是辛钦伯努利大数定律的一个特例。

3、切比雪夫大数定律：揭示了样本均值和真实期望的关系

设X1,X2,⋯是相互独立的随机变量序列，且它们的期望值存在，记为E(Xi)=μ(i=1,2,⋯)，有方差存在且有共同有限上界

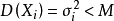
，则对 任意的ɛ>0，有

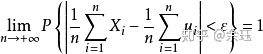
特别的，若Xi有相同的期望

，则有

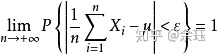
为用统计方法来估计期望提供了理论依据。

相较于辛钦大数定律，切比雪夫大数定理并未要求同分布，更具一般性。

总结如下：

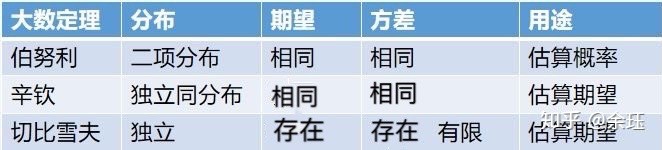
总结来看，大数定理将属于数理统计的平均值和属于概率论的期望联系在了一起。