初次接触矩阵乘法时,你是否感觉和矩阵加法相比,矩阵乘法不仅怪异而且枯燥繁复。这不怪你,这种方法适合电脑计算,却不适合人脑理解。以矩阵-向量乘法为例,大部分教科书从行的角度来计算:
这种以行为主的思想进行内积运算,也称点积运算,将左矩阵(
![]()
)第1行和右矩阵(
![]()
)第1列(上例是向量,可视为1列的矩阵,
![]()
)进行点积,进行
![]()
次乘法和
![]()
次加法才得到结果矩阵的第1行第1列元素
![]()
:
![]()
,这种计算方式颗粒度太细,机器运算起来非常高效,却不利于我们理解;从更高的维度 ——
列向量来看,结果相同但更清晰:
以列为主的视角将矩阵乘法视为对矩阵的列向量进行线性组合,这是线性代数非常重要的本质和基础,并很自然地引出了列空间的概念。
我们知道:两条相交的直线确定一个平面。
![]()
为任意实数,
![]()
能组合出一个
![]()
的2维平面空间内的任何向量,显然,该平面只是3维空间
![]()
中无数平面中的一个(子空间),但对于位于该平面内的任意向量
![]()
, 一定存在
![]()
,使得
![]()
,该平面是这两个向量所张成(Span)的
列空间(Column Space),这两个向量是列空间的基(Basis),通过对基的线性组合,可以得到空间内的任意向量,难怪有人说线代是"搞基"。
列空间由矩阵
的列向量线性组合(Linear Combination)填充而成,记为
。
线性代数的初心和核心是求解
![]()
,
![]()
是
![]()
的矩阵,以列向量表示:
![]()
,
![]()
和
![]()
分别是
![]()
和
![]()
的向量,
![]()
位于
![]()
的列空间时,
![]()
一定存在解
![]()
将
![]()
表达为
![]()
的列向量线性组合
![]()
。
u,v通过线性组合张成的空间
如果
![]()
位于
![]()
的列空间
之外,问题变成了常规的
线性回归,列向量无论进行怎样的线性组合都不可能组合出平面外的
![]()
,此题无解,我们退而求其次,找一个近似解
![]()
,使
![]()
尽量靠近
![]()
,但必须在平面(列空间)内,显然,
![]()
在平面的
投影是平面内离
![]()
最近的那个点,具体可参考Normal Equation的向量投影解法与几何和直觉解释。
P.S. 机器学习场景中,
![]()
的行数和列数分别对应样本数和特征(字段)数量,样本数往往远大于特征量(图像问题相反),比如1000个样本10个特征,小学数学多元一次方程组的知识告诉我们:1000个方程只有10个变量是无解的,被称为超定(Overdetermined)。
本质上,机器学习算法提供的不是数学意义上准确解,而是个实用主义的近似解,毕竟,比无解要好很多。
顺便提一句,当你拿起一本线性代数书籍,如果第一章是行列式,建议立刻马上放下它,因为它会浪费你的时间,加大你理解矩阵的难度。
*本文主要思想来自Gilbert Strange的18.06。

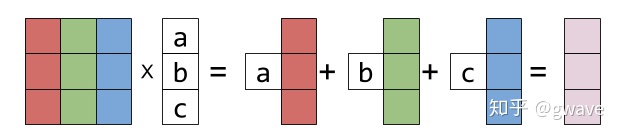







 本文探讨矩阵乘法的核心思想,从列空间的角度出发,解释矩阵乘法实际上是矩阵列向量的线性组合。列空间的概念对于理解线性方程组的解至关重要。机器学习中,算法寻求的是实用主义的近似解。建议学习线性代数时避开以行列式开篇的书籍。
本文探讨矩阵乘法的核心思想,从列空间的角度出发,解释矩阵乘法实际上是矩阵列向量的线性组合。列空间的概念对于理解线性方程组的解至关重要。机器学习中,算法寻求的是实用主义的近似解。建议学习线性代数时避开以行列式开篇的书籍。
















 2737
2737

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








