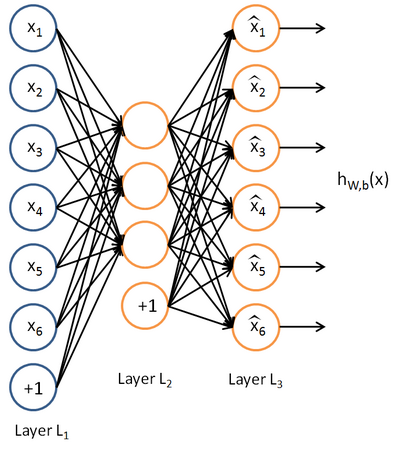
自编码算法是一种非监督学习,可以理解为通过神经网络尝试学习一个函数使得输出等于输入
如图输入层和输出层各有6个神经元,隐藏层有3个神经元,这个网络就是学习了一个数据的压缩表示,它能通过3个(维)的隐藏神经元重构出6个(维)输出神经元的数据。
如果网络的输入数据是完全随机的,比如每一个输入
![]() 都是一个跟其它特征完全无关的独立同分布高斯随机变量,那么这一压缩表示将会非常难学习。但是如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性(就是这么神奇)。
都是一个跟其它特征完全无关的独立同分布高斯随机变量,那么这一压缩表示将会非常难学习。但是如果输入数据中隐含着一些特定的结构,比如某些输入特征是彼此相关的,那么这一算法就可以发现输入数据中的这些相关性(就是这么神奇)。
事实上,这一简单的自编码神经网络通常可以学习出一个跟主元分析(PCA)结果非常相似的输入数据的低维表示。
当隐藏神经元较多的时候,可以加入稀疏性的限制学习到一些有趣的东西。在介绍稀疏性之前先引入活跃度的概念,当一个神经元的激活函数输出接近最大值时(sigmoid是1,tanh是1)称这个神经元是被激活的;当一个神经元的激活函数输出接近最小值时(sigmoid是0,tanh是-1)称这个神经元是被抑制的。
这样我们就可以算出隐藏层神经元的平均激活度
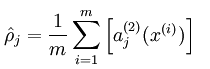
然后对这个平均激活度加以限制,限制通常是一个接近于0的较小的数
为了实现这个限制,要在目标优化函数中加入一个额外的惩罚因子,惩罚因子有很多种,以下是其中一种
(当rho非常大时,主要起作用的就是式子中的前半段,这个惩罚因子也会非常大,当rho非常小时,式子中的前半段也非常小,后半段中近似为log1,也就是0,整个惩罚因子也就变得非常小)
其实这个惩罚因子也就
是一个以
 为均值和一个以
为均值和一个以
 为均值的两个伯努利随机变量之间的相对熵
为均值的两个伯努利随机变量之间的相对熵
 为均值和一个以
为均值和一个以
 为均值的两个伯努利随机变量之间的相对熵
为均值的两个伯努利随机变量之间的相对熵
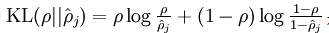
应用:当我们对稀疏自编码器(100个隐藏单元,在10X10像素的输入上训练 )进行上述可视化处理之后,发现不同隐藏神经元学到的是不同的位置和方向的边缘检测,以下是一个简易版的结果:







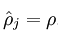
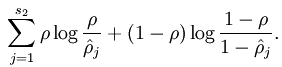

















 9380
9380

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








