矩形函数的傅里叶变换_用图解的方法解读傅里叶变换的本质原理

前面的文章我们详细的从另一个角度来解读傅里叶变换，傅里叶变换为非周期函数的处理提供了强有力的数学工具，我们用欧拉公式将e的指数项分解为实数和虚数两部分

我们以矩形函数为例，这个矩形函数的T=∞，左边对应的是实数情况下的余弦波，右边对应的是复数情况下的正弦波函数，我们来看这个波形是如何与傅里叶变换对应的

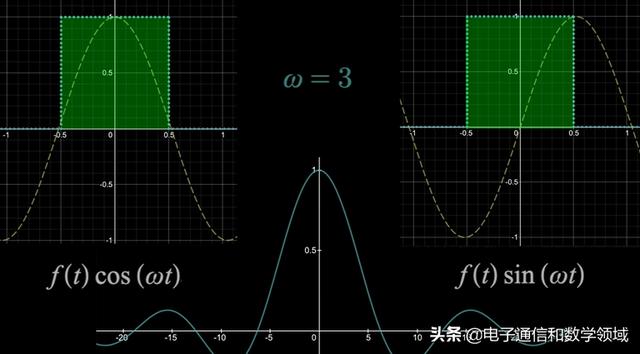
因为矩形波在-0.5

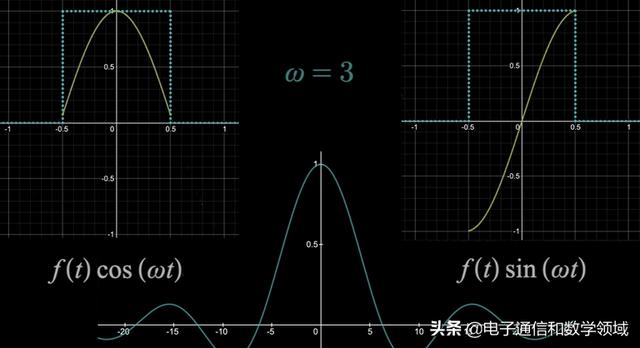
正余弦阴影区域的面积之和就是我们要得到的傅里叶变换

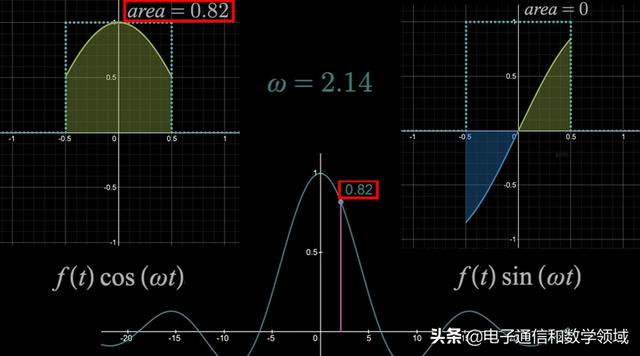
如下，当角频率ω=2.14时，左边图形下的面积=0.82，右边等于0，所以ω=2.14时傅里叶变换就等于0.82

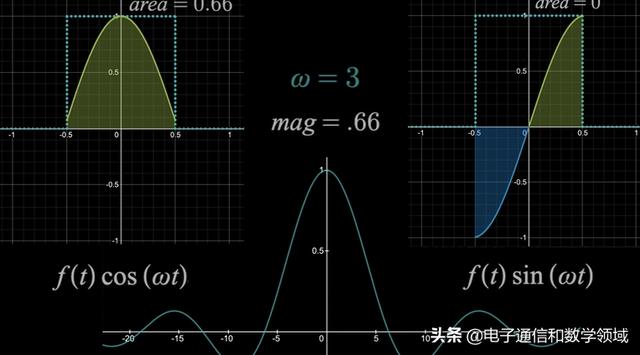
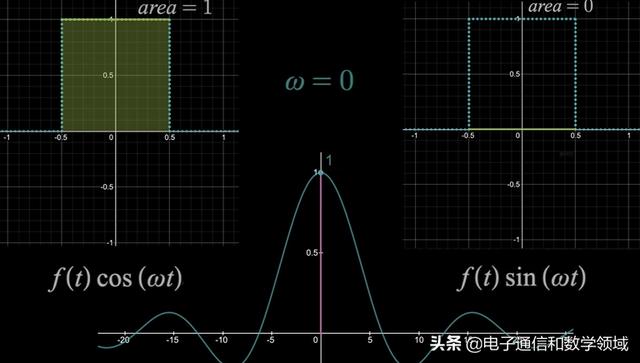
但有一个有趣的结论：ω=0时，傅里叶变换的值就是原函数曲线下的面积，如下图面积等于1，但右边的波形区域下的面积始终等于0

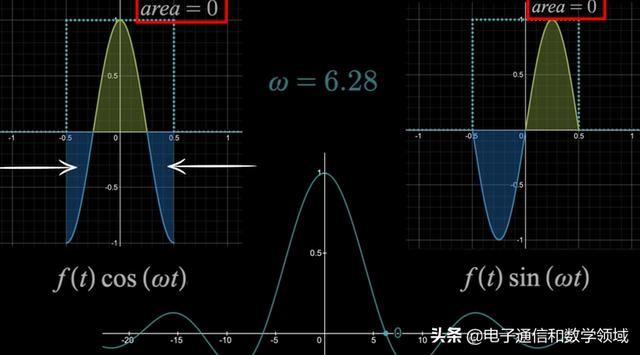
我们继续，当ω=6.28=2π时，左边的余弦波图形是一个完整的周期函数，所以面积等于0，右边的正弦波函数图形仍然等于0

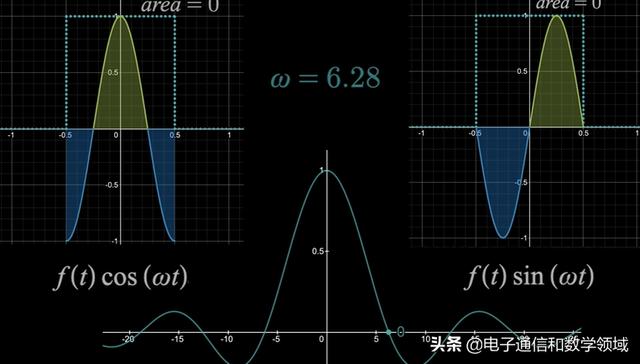
所以ω=0时，傅里叶变换F(ω)的值等于0

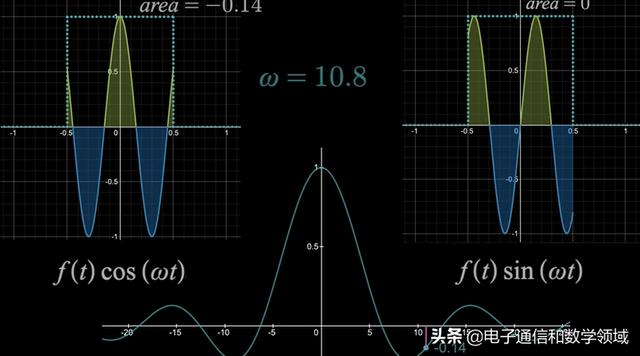
当ω=10.8，左边正弦波下的面积是-0.14，所以F(ω)=-0.14

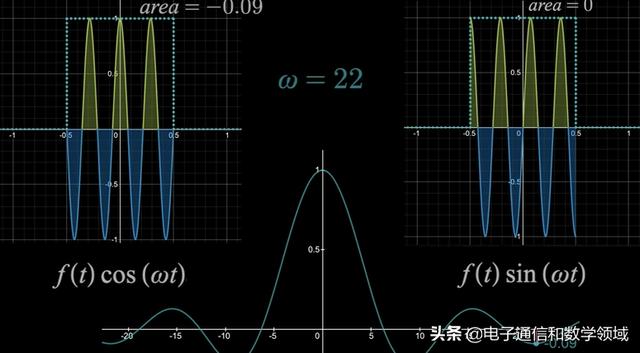
当ω=22时，左边正弦波下的面积是-0.09，右边图形下的面积始终等于0，所以F(ω)=--0.09，