spss正态性检验_SPSS中的正态性检验之二：计算法

上一节，我们介绍了用图示法来检验样本的正态分布性，这一节，我们介绍用计算法来检验样本的正态分布性。

一、偏度系数和峰度系数的计算

我们知道，偏度系数和峰度系数是了解资料正态分布的指标，两者越接近0，资料就越接近正态分布。在SPSS中，很多过程都可以完成偏度系数和峰度系数的计算，我们介绍用“描述统计”功能计算偏度系数和峰度系数。

1. 建立数据集

2. 操作步骤，点击“选项”-“峰度”-“偏度”

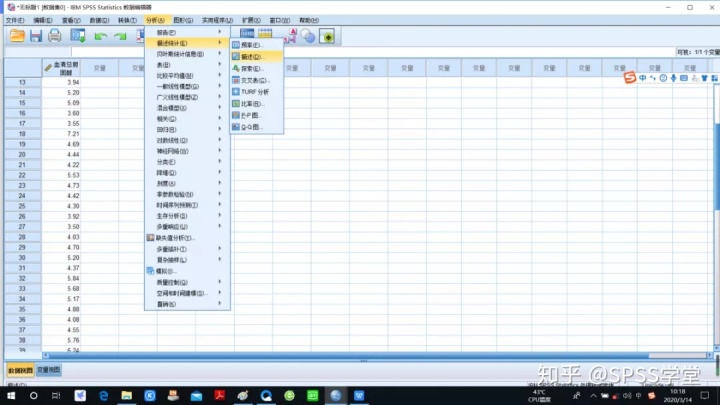
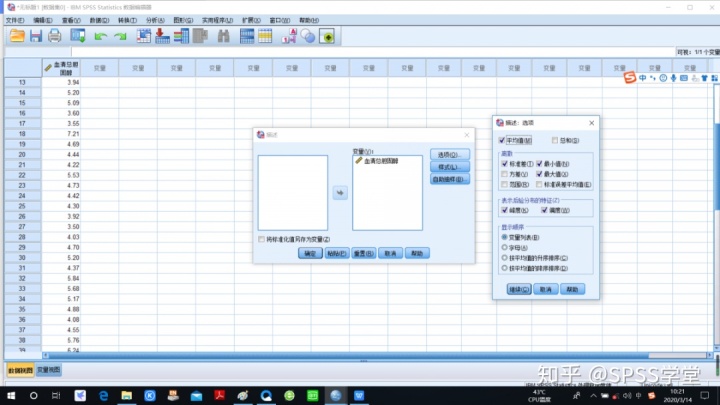
3. 结果分析

结果的最后两列是偏度系数和峰度系数的点估计值和各自的标准误，大致可以看出，二者的95%置信区间（统计量±1.96标准误）都包括0，所以可以初步判断资料服从正态分布。

二、Kolmogorov-Smirnov检验与Shapiro-Wilk检验

Kolmogorov-Smirnov检验是一种非参数检验方法，可以对单样本的拟合优度进行检验，推断样本是否来自正态分布总体、均匀分布总体或Poisson分布总体等，其特点是速度快，便于计算机实现。一般适用于大样本。

Shapiro-Wilk检验也简称为W检验，是S.S.Shapiro与M.B.Wilk于1933年提出，常用于样本量在3~50之间数据的正态性检验。

1.建立数据集

2.在SPSS中运用“探索”过程对资料的正态性进行Kolmogorov-Smirnov检验与Shapiro-Wilk检验

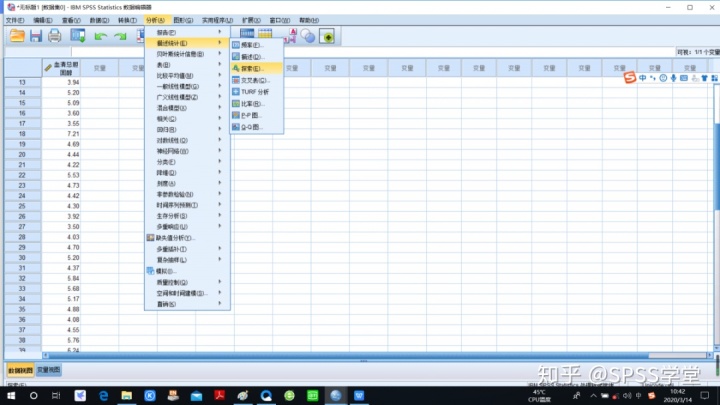
3.“图”-勾选“含检验的正态图”

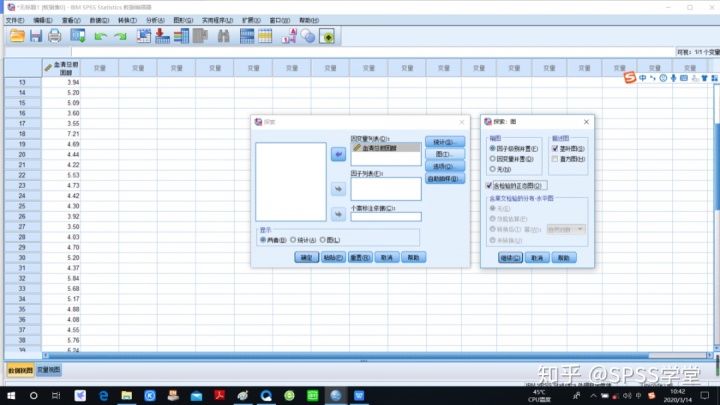
4. 结果判读

从结果可以看出，无论是Kolmogorov-Smirnov检验，还是Shapiro-Wilk检验，其检验统计量对应的p值均＞0.05，表明资料服从正态分布。

同时，SPSS还输出了正态性Q-Q图和去趋势的Q-Q图结果，从图上看，也提示数据服从正态分布。详情见上期内容