如何将有向图转化为无向图_有向图的学习笔记1 动态更新

最近山东大学开展了 有向图的讨论课程，我在这也总结一些我研究生上课时候用的教材和这次学习的体会，机会难得，非常期待第二本书的作者Jorgen Bang-Jensen讲 网络流这一块，这一块我一直理解的不透彻。借着这次机会学习。我主要用下面两本的教材：

1 教材分析 （不断更新）

例1：

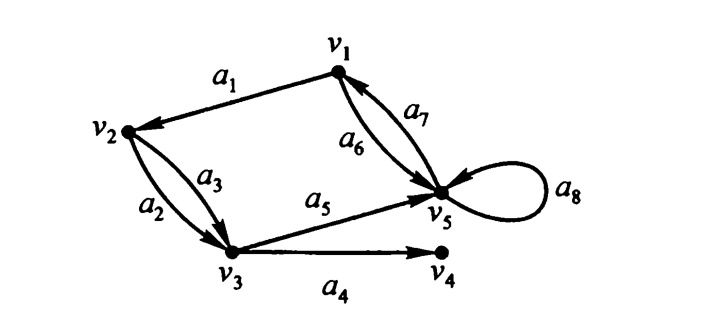
图中

是环弧，

是平行弧，

作为反向弧。

可以用例1的例子尝试解释上面说的概念。注意

的出度是2，入度为3.

下面定理前半部分 顶点的度和等于边数的两倍，类似于无向图的 握手引理。 定理8.1.1 对于任何有向图

,都有

且

定义8.1.5 与有向图的概念相对应，边不带有方向的图称为无向图．
给定一个无向图

,给它的每条边

确定一个方向，便可得到一个有向图， 这个有向图称为

的一个

定向图，而

称为这个有向图的

基础图或 底图 (underlying graph).

定义8.2.1有向图的一条有向途径是指一个有限非空序列

，它的各项交替地是顶点和弧，使得

．弧不重复的有向途径称为有向迹；顶点不重复的有向途径称为有向路；首尾相接的有向路称为有向圈．

注 有向图的底图中有长的路未必该有向图中就有长的有向路．例如，下图所示的有向图 其底图中的最长路为6，但其最长有向路的长为1.

令人惊奇的是，有向图中·有向路的长却与其底图的色数有关．

定理8.2.1 (Vitaver, 1962; Roy, 1967; Gallai, 1968) 以图

为底图的有向图