python 线性回归_Python机器学习之“线性回归”

      如果说朴素贝叶斯是解决分类任务的好起点，那么线性回归模型就是解决回归任务的好起点。这些模型之所以大受欢迎，是因为它们的拟合速度非常快，而且很容易解释。你可能对线性回归模型最简单的形式(即对数据拟合一条直线)已经很熟悉了，不过经过扩展，这些模型可以对更复杂的数据行为进行建模。

      本次将先快速直观地介绍线性回归问题背后的数学基础知识，然后介绍如何对线性回归模型进行一般化处理，使其能够解决数据中更复杂的模式。首先导入常用的程序库：

%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np

01 / 简单线性回归

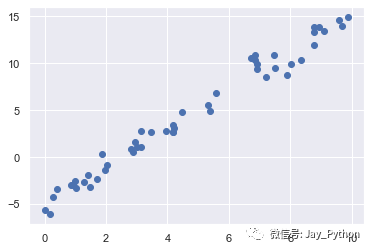
      首先来介绍最广为人知的线性回归模型——将数据拟合成一条直线。直线拟合的模型方程为 y = ax + b，其中 a 是直线斜率，b 是直线截距。看看下面的数据，它们是从斜率为 2、截距为 -5 的直线中抽取的散点：

rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = 2 * x - 5 + rng.randn(50)
plt.scatter(x, y);

可以用 Scikit-Learn 的 LinearRegression 评估器来拟合数据，并获得最佳拟合直线：

from sklearn.linear_model import LinearRegression
model = LinearRegression(fit_intercept=True)

model.fit(x[:, np.newaxis], y)

xfit = np.linspace(0, 10, 1000)
yfit = model.predict(xfit[:, np.newaxis])

plt.scatter(x, y)
plt.plot(xfit, yfit);

数据的斜率和截距都在模型的拟合参数中，Scikit-Learn 通常会在参数后面加一条下划线，即 coef_ 和 intercept_：

print("Model slope:    ", model.coef_[0])
print("Model intercept:", model.intercept_)

Model slope:     2.0272088103606944
Model intercept: -4.9985770855532

     可以看到，拟合结果与真实值非常接近，这正是我们想要的。

      然而，LinearRegression 评估器能做的可远不止这些——除了简单的直线拟合，它还可以处理多维度的线性回归模型：

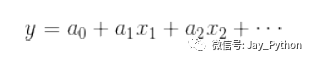
      里面有多个 x 变量。从几何学的角度看，这个模型是拟合三维空间中的一个平面，或者是为更高维度的数据点拟合一个超平面。

     虽然这类回归模型的多维特性使得它们很难可视化，但是我们可以用NumPy 的矩阵乘法运算符创建一些数据，从而演示这类拟合过程：

rng = np.random.RandomState(1)
X = 10 * rng.rand(100, 3)
y = 0.5 + np.dot(X, [1.5, -2., 1.])

model.fit(X, y)
print(model.intercept_)
print(model.coef_)

0.50000000000001
[ 1.5 -2.   1. ]

其中 y 变量是由 3 个随机的 x 变量线性组合而成，线性回归模型还原了方程的系数。

通过这种方式，就可以用一个 LinearRegression 评估器拟合数据的回归直线、平面和超平面了。虽然这种方法还是有局限性，因为它将变量限制在了线性关系上，但是不用担心，还有其他方法。

02 / 基函数回归

你可以通过基函数对原始数据进行变换，从而将变量间的线性回归模型转换为非线性回归模型。这个方法的多维模型是：

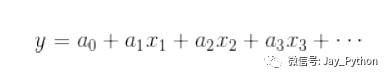
需要注意的是，这个模型仍然是一个线性模型，也就是说系数 a n 彼此不会相乘或相除。我们其实是将一维的 x 投影到了高维空间，因此通过线性模型就可以拟合出 x 与 y 间更复杂的关系。

2-1. 多项式基函数

多项式投影非常有用，因此 Scikit-Learn 内置了PolynomialFeatures 转换器实现这个功能：

from sklearn.preprocessing import PolynomialFeatures
x = np.array([2, 3, 4])
poly = PolynomialFeatures(3, include_bias=False)
poly.fit_transform(x[:, None])

array([[ 2.,  4.,  8.],
       [ 3.,  9., 27.],
       [ 4., 16., 64.]])

转换器通过指数函数，将一维数组转换成了三维数组。这个新的高维数组之后可以放在多项式回归模型中。

和之前一样，最简洁的方式是用管道实现这些过程。

让我们创建一个 7 次多项式回归模型：

from sklearn.pipeline import make_pipeline
poly_model = make_pipeline(PolynomialFeatures(7),
                           LinearRegression())

数据经过转换之后，我们就可以用线性模型来拟合 x 和 y 之间更复杂的关系了。例如，下面是一条带噪的正弦波：

rng = np.random.RandomState(1)
x = 10 * rng.rand(50)
y = np.sin(x) + 0.1 * rng.randn(50)

poly_model.fit(x[:, np.newaxis], y)
yfit = poly_model.predict(xfit[:, np.newaxis])

plt.scatter(x, y)
plt.plot(xfit, yfit);

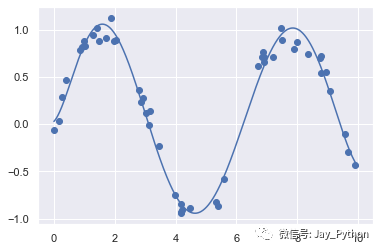
     通过运用 7 次多项式基函数，这个线性模型可以对非线性数据拟合出极好的效果！

2-2. 高斯基函数

      当然还有其他类型的基函数。例如，有一种常用的拟合模型方法使用的并不是一组多项式基函数，而是一组高斯基函数。最终结果如图所示：

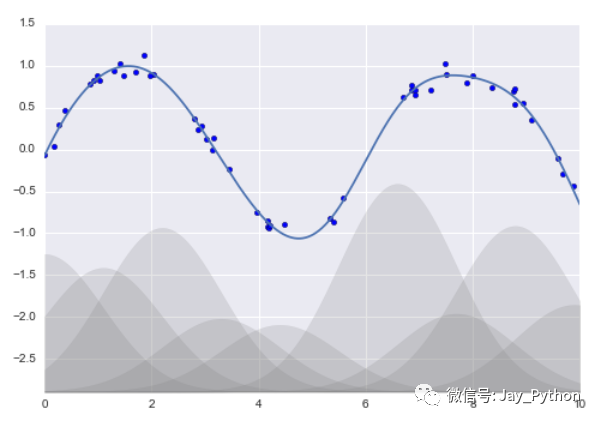
图中阴影部分代表不同规模基函数，把它们放在一起时就会产生平滑的曲线。 Scikit-Learn 并没有内置这些高斯基函数，但我们可以自己写一个转换器来创建高斯基函数，效果如下图所示(Scikit-Learn 的转换器都是用 Python 类实现的，阅读 Scikit-Learn 的源代码可能更好地理解它们的创建方式)：

from sklearn.base import BaseEstimator, TransformerMixin

class GaussianFeatures(BaseEstimator, TransformerMixin):
   """一维输入均匀分布的高斯特征"""

    def __init__(self, N, width_factor=2.0):
        self.N = N
        self.width_factor = width_factor

    @staticmethod
    def _gauss_basis(x, y, width, axis=None):
        arg = (x - y) / width
        return np.exp(-0.5 * np.sum(arg ** 2, axis))

    def fit(self, X, y=None):
        ## 在数据区间中创建N个高斯分布中心
        self.centers_ = np.linspace(X.min(), X.max(), self.N)
        self.width_ = self.width_factor * (self.centers_[1] - self.centers_[0])
        return self

    def transform(self, X):
        return self._gauss_basis(X[:, :, np.newaxis], self.centers_,
                                 self.width_, axis=1)

gauss_model = make_pipeline(GaussianFeatures(20),
                            LinearRegression())
gauss_model.fit(x[:, np.newaxis], y)
yfit = gauss_model.predict(xfit[:, np.newaxis])

plt.scatter(x, y)
plt.plot(xfit, yfit)
plt.xlim(0, 10);




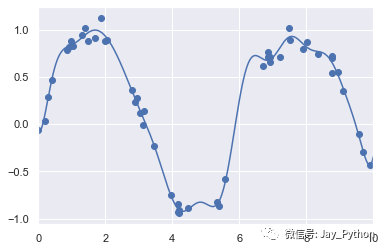
我们之所以将这个示例放在这里，是为了演示多项式基函数并不是什么魔法：如果你对数据的产生过程有某种直觉，那么就可以自己先定义一些基函数，然后像这样使用它们。

03 / 正则化

虽然在线性回归模型中引入基函数会让模型变得更加灵活，但是也很容易造成过拟合。例如，如果选择了太多高斯基函数，那么最终的拟合结果看起来可能并不好：

model = make_pipeline(GaussianFeatures(30),
                      LinearRegression())
model.fit(x[:, np.newaxis], y)

plt.scatter(x, y)
plt.plot(xfit, model.predict(xfit[:, np.newaxis]))

plt.xlim(0, 10)
plt.ylim(-1.5, 1.5);

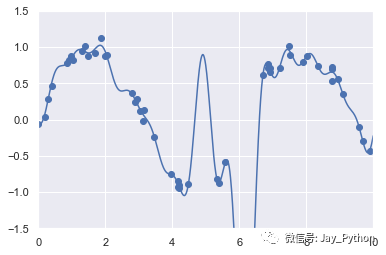
      如果将数据投影到 30 维的基函数上，模型就会变得过于灵活，从而能够适应数据中不同位置的异常值。如果将高斯基函数的系数画出来，就可以看到过拟合的原因。

def basis_plot(model, title=None):
    fig, ax = plt.subplots(2, sharex=True)
    model.fit(x[:, np.newaxis], y)
    ax[0].scatter(x, y)
    ax[0].plot(xfit, model.predict(xfit[:, np.newaxis]))
    ax[0].set(xlabel='x', ylabel='y', ylim=(-1.5, 1.5))

    if title:
        ax[0].set_title(title)

    ax[1].plot(model.steps[0][1].centers_,
               model.steps[1][1].coef_)
    ax[1].set(xlabel='basis location',
              ylabel='coefficient',
              xlim=(0, 10))

model = make_pipeline(GaussianFeatures(30), LinearRegression())
basis_plot(model)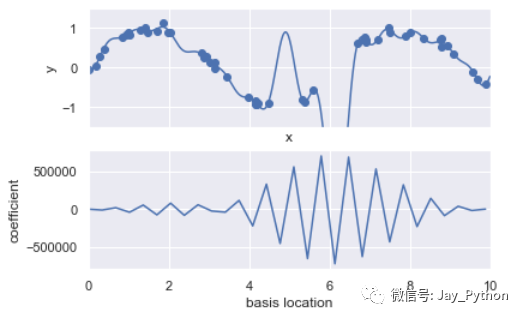

     下面那幅图显示了每个位置上基函数的振幅。当基函数重叠的时候，通常就表明出现了过拟合：相邻基函数的系数相互抵消。这显然是有问题的，如果对较大的模型参数进行惩罚(penalize)，从而抑制模型剧烈波动，应该就可以解决这个问题了。这个惩罚机制被称为正则化(regularization)，有几种不同的表现形式。

3-1. 岭回归(L 2 范数正则化)

正则化最常见的形式可能就是岭回归(ridge regression，或者 L 2 范数正则化)，有时也被称为吉洪诺夫正则化(Tikhonovregularization)。其处理方法是对模型系数平方和(L 2 范数)进行惩罚，模型拟合的惩罚项为：

其中，α 是一个自由参数，用来控制惩罚的力度。这种带惩罚项的模型内置在 Scikit-Learn 的 Ridge 评估器中：

from sklearn.linear_model import Ridge
model = make_pipeline(GaussianFeatures(30), Ridge(alpha=0.1))
basis_plot(model, title='Ridge Regression')

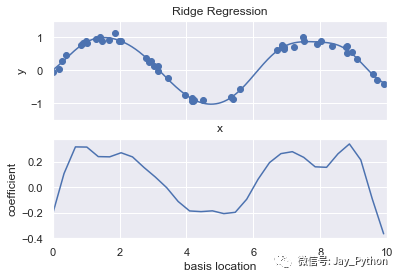
参数 α 是控制最终模型复杂度的关键。

• 如果 α → 0，那么模型就恢复到标准线性回归结果；

• 如果 α →∞，那么所有模型响应都会被压制。

岭回归的一个重要优点是，它可以非常高效地计算——因此相比原始的线性回归模型，几乎没有消耗更多的计算资源。

3-2. Lasso正则化(L 1 范数正则化)

   另一种常用的正则化被称为 Lasso，其处理方法是对模型系数绝对值的和(L 1 范数)进行惩罚：

虽然它在形式上非常接近岭回归，但是其结果与岭回归差别很大。

例如，由于其几何特性，Lasso 正则化倾向于构建稀疏模型；也就是说，它更喜欢将模型系数设置为 0。

from sklearn.linear_model import Lasso
model = make_pipeline(GaussianFeatures(30), Lasso(alpha=0.001))
basis_plot(model, title='Lasso Regression')

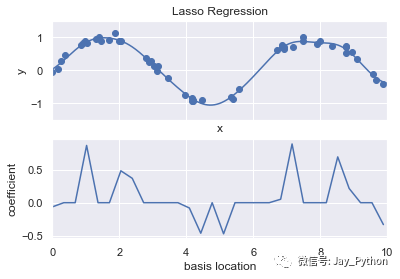
      通过 Lasso 回归惩罚，大多数基函数的系数都变成了 0，所以模型变成了原来基函数的一小部分。与岭回归正则化类似，参数 α 控制惩罚力度，可以通过交叉检验来确定。

欢迎关注、转发、评论