三维坐标投影到二维平面_Python-OpenCV 12. 透视投影与透视变换

本文学习资源《机器学习实践指南 案例应用解析》

一、 原理

三维计算机图形学中，投影可以看作是一种将三维坐标变换为二维坐标的方法，常用到的有正交投影和透视投影。

正交投影多用于三维健模，透视投影则由于和人的视觉系统相似，多用于在二维平面中对三维世界的呈现。

与平行投影沿着平行线将物体投影到图像平面不同，透视投影是指从投影中心这一点发出的直线将物体投影到图像平面上。这就意味着距离投影中心越远的投影越小，距离越近的投影越大。

透视投影基本模型：

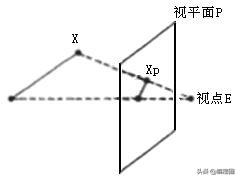
二、OpenCV的实现

1. WarpPerspective

OpenCV提供了WarpPerspective函数，可对图像进行透视变换:

cv2.warpPerspective(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) -> dst

主要参数说明：

• map_matrix： 3x3变换矩阵
• flags：插值方法和以下开关选项的组合，有以下两种：
• CV_WARP_FILL_OUTLIERS 填充所有缩小图像的像素。如果部分像素落在输入图像的边界外，那么它们的值设定为fillval。
• CV_WARP_INVERSE_MAP：指定matrix是输出图像到输入图像的反变换，因此可以直接用来做像素插值。否则，函数从map_matrix得到反变换。
• fillval：用来填充边界外面的值。

2. GetPerspectiveTransform

以四边形的4个点计算透射变换：

cv2.getPerspectiveTransform(src,dst) -> retval

• src：输入IDR的四边形顶点坐标
• dst：输出的相应的四边形顶点坐标

3. 代码实例

# -*- coding: utf-8 -*-import cv2import numpy as npfn = "test.jpg"img = cv2.imread(fn)cv2.imshow('source', img)w = img.shape[1]h = img.shape[0]# 得到透射变换矩阵src = np.array([[0, 0], [w - 1, 0], [w - 1, h - 1], [0, h - 1]], dtype=np.float32)dst = np.array([[w * 0.08, h * 0.01], [w * 0.8, h * 0.25], [w * 0.8, h * 0.9], [w * 0.05, h * 0.8]], dtype=np.float32)transform_matrix = cv2.getPerspectiveTransform(src, dst)print(transform_matrix)# 透射变换完成变形newimg = cv2.warpPerspective(img, transform_matrix, (w, h))cv2.imshow('preview', newimg)cv2.waitKey()cv2.destroyAllWindows()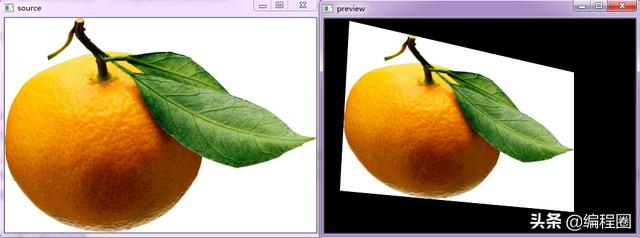

三、图像矫正实例

import cv2import numpy as npimport matplotlib.pyplot as pltimg = cv2.imread('test.png')H_rows, W_cols = img.shape[:2]print(H_rows, W_cols)# 原图中书本的四个角点(左上、右上、左下、右下),与变换后矩阵位置pts1 = np.float32([[135, 65], [739, 316], [50, 1065], [848, 1134]])pts2 = np.float32([[55, 65], [842, 65], [55, 1065], [842, 1065], ])# 生成透视变换矩阵；进行透视变换M = cv2.getPerspectiveTransform(pts1, pts2)dst = cv2.warpPerspective(img, M, (W_cols, H_rows))plt.subplot(121), plt.imshow(img[:, :, ::-1]), plt.title('input')plt.subplot(122), plt.imshow(dst[:, :, ::-1]), plt.title('output')plt.show()