正态分布是离散分布还是连续分布_简单统计学|正态分布之连续数据的概率分布...

到目前为止，我们接触到的都是可以指定确切数值的概率分布。然而并非所有数据 集合都是如此，还有几类数据并不符合我们之前遇到的概率分布。我们将在这一章 里讲解所谓的连续型概率分布，并介绍最重要的概率分布类型之一——正态分布。

1. 离散分布并非无所不能

离散数据可取确切值

前面讲到的概率分布涉及的都是离散数据，即数据由一个个单独的数值组成，其中的每一个数值都有相应概率。离散数据往往能以某种方式进行计数，例如糖果机中的糖果数目，智力游戏中答对的问题的数目，或是机器在一个特定时段内的故障次数。

但并非所有数值型数据都是离散的

列举一个数据集中的所有数值并不总是能够实现。有时候，数据涵盖的是一个范围，这个范围内的任何一个数值都有可能成为事件结果。

例如，假定有人让你精确地测量几段丝线的长度，并且已知这些丝线的长度在10英寸到11英寸之间，你的测量结果可能会是10英寸、10.1英 寸、10.01英寸，等等，因为丝线长度可以是这个范围内的任意值。

这样的数据叫做连续数据，连续数据往往通过测量得到，而不是通过计数得到，测量结果在很大程度上取决于测量精度要求。

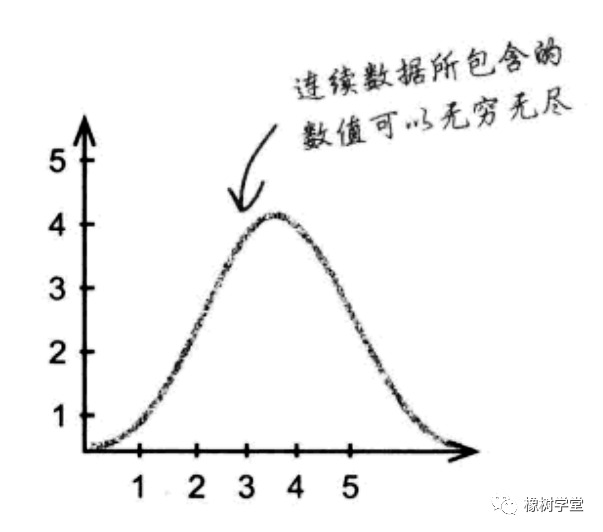
2. 连续数据的概率分布

前面我们讲过：离散数据可以通过计数做出频数(频率)表，绘制出频率分布图(很细的柱状图)，只不过纵坐标不是频数，而是频率。这些横坐标上所有数值或类别对应的频率之和等于1。

对于离散概率分布来说，我们关心的是取得一个特定数值的概率；而对于连续概率分布来说，我们关心的是取得一个特定范围的概率。例如：身高在160-170cm范围的概率。

概率密度函数可用于描述连续数据

我们可以用概率密度函数描述连续性随机变量的概率分布。

概率密度函数f(x)是这样一种函数：通过它可以求出一个数据范围内的某个连续变量的概率，它向我们指出该概率分布的形状。

我学习了2年的微积分终于可以派上用场了。

概率=面积

连续随机变量的概率通过面积表示。为了求出一个特定数值范围的概率，首先可画出概率密度函数，位于函数图形下方且介于这个特定数值范围之间的面积就是这个特定数值范围的概率。

我必须用面积求概率吗？不能把那个范围里的数值一个一个选出来，再把这些数值的概率加起来吗？以前离散概率就是这么求的？

这种做法不适用于连续概率

就好像不同于，对于连续概率，我们必须通过计算概率密度曲线下方的面积得出概率。

---

有问必答

• 问: 有一种函数叫做概率密度函数，那么什么是概率密度?

• 答: 概率密度指出各种范围内的概率的大小，通过概率密度函数进行描述。它与我们在第一章碰到过的频数密度十分相似。概率密度通过面积标示概率大小，而频数密度通过面积标示频数大小。

• 问: 难道概率密度和概率不是一回事?

• 答: 概率密度是一种表示概率的方法，但它并非概率本身。概率密度函数是图形中的一条线条，而概率则是这条线下方的一定数值范围内的面积。

• 问: 关于概率范围，你已经讲过不少。我如何求出一个精确数值的概率?

• 答: 在处理连续数据的时候，实际上考虑的是一个可以接受的精度，并且基于这些数值形成一个范围。让我们看一个例子: 假定你想要一段丝线，长度10英寸，精确到英寸。虽然“你需要一段正好长10英寸的丝线”这种说法最容易脱口而出，但这并不完全正确。你真正想要的是一段长度介于9.5英寸到10.5英寸之间的丝线，因为你想让这段10英寸长的丝线“精确到英寸”。即，你想求出长度介于9.5英寸到10.5英寸这个范围内的概率。

• 问: 如果我想求连续数据某一个精确的数值的概率，会是多少?

• 答: 结果为0——猛一听可能会觉得有违直觉，但你的问题其实可以这样理解:求一个具有无穷小数位数的精确数值的概率。让我们再以丝线长度为例:如果你需要一段长度正好等于10英寸的丝线，会出现什么局面?——你会需要用一台高倍放大镜，以原子大小为精度，量出一段10英寸长的丝线，“丝线的长度正好为10英寸”这个事件基本上不可能发生。也就是其概率为零。

END

大家感兴趣的话可以跟着一起学，更多R语言数据分析及可视化内容，长按或扫描下方二维码关注“橡树学堂”详细了解：

关注橡树学堂，每天学一点R语言，让我们爱上数据分析可视化