正态分布相关的那些事儿

《概率论和数理统计》中将正态分布定义为用来描述连续型随机变量的一个密度函数，解决正态分布的时候要做标准化；对于这个密度函数我们应该关注哪些事儿呢？（教材中很多故弄玄虚，卖弄概念的东西很不好理解）

• 概率论中如何分类随机变量的？离散和连续型随机变量的概率值如何描述的？（分布律、随机变量概率函数、分布函数、密度函数）,不同类型的随机变量概率描述选择不同的函数的内因是什么？
• 连续性随机变量的概率取值函数—概率密度函数之正态分布型概率密度函数
• 什么样的概率特征符合正态分布？均值&标准差作用是什么？如何计算正态分布密度函数的概率值（标准正态分布）；
• 正态分布的概率密度函数 在用于决策中的实际场景有哪些？

一、如何理解概率分布函数和概率密度函数

1、从离散型随机变量和连续型随机变量说起

举个栗子：

• 一批设备中故障设备的数目。

• 同样一批设备，他们寿命情况。

第一个例子中，故障设备的数量在现实中是肉眼可见，能够区分出的；但是第二个栗子中，寿命是一个无法用肉眼数过来的数字，它需要记录下来，变成一个数字你才能感受它。这里第一个栗子就是离散型随机变量，第二个涉及的变量就是连续型随机变量；

在贾俊平老师的《统计学》教材中，给出了这样的区分：

如果随机变量的值可以都可以逐个列举出来，则为离散型随机变量。如果随机变量X的取值无法逐个列举则为连续型变量

确实不太好理解，用一个不太严谨的描述，辅助理解：只要是能够用我们日常使用的量词可以度量的取值，比如次数，个数，块数等都是离散型随机变量。只要无法用这些量词度量，且取值可以取到小数点2位，3位甚至无限多位的时候，那么这个变量就是连续型随机变量！

贾俊平还有一句话值得细品，也可以辅助理解：

如果微积分是研究变量的数学，那么概率论与数理统计是研究随机变量的数学。

2、再理解离散型随机变量的概率分布，概率函数和分布函数

先来理解下离散型随机变量的概率分布和概率函数，长得差不多，含义也差不多！

在讲概率函数和概率分布之前，我想先讲讲为什么我们花这么大的力气去研究这个概念。因为它实在太重要了，为什么呢？在这里，我直接引用陈希孺老师在他所著的《概率论与数理统计》这本书中说的，核心理念：

研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何！

我们后续接触的所有概念，什么概率函数、概率密度、概率分布，都是在描述随机变量的概率！概率！概率！

（1）、概率函数：用函数的形式来表达概率（课本中其实也叫分布律）

pi=P(X=ai)(i=1,2,3,4,5,6)

在这个函数里，自变量（X）是随机变量的取值，因变量（pi）是取值的概率。这就叫啥，这叫用数学语言来表示自然现象！它就代表了每个取值的概率，所以顺理成章的它就叫做了X的概率函数。从公式上来看，概率函数一次只能表示一个取值的概率。比如P（X=1）=1/6,这代表用概率函数的形式来表示，当随机变量取值为1的概率为1/6，一次只能代表一个随机变量的取值。

（2）、概率分布：顾名思义就是概率的分布

理解这个概念时，关键不在于“概率”两个字，而在于“分布”这两个字。为了理解“分布”这个词，我们来看一张图。

在很多教材中，这样的列表都被叫做离散型随机变量的“概率分布”。其实严格来说，它应该叫“离散型随机变量的值分布和值的概率分布列表”，这个名字虽然比“概率分布”长了点，但是对于我们这些笨学生来说，肯定好理解了很多；

举个例子吧，一颗6面的骰子，有1，2，3，4，5，6这6个取值，每个取值取到的概率都为1/6。那么你说这个列表是不是这个骰子取值的”概率分布“？

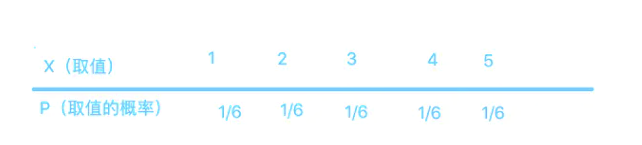
长得挺像的，上面是取值，下面是概率，这应该就是骰子取值的“概率分布”了吧！大错特错！少了一个最重要的条件！对于一颗骰子的取值来说，它列出的不是全部的取值，把6漏掉了!

（3）、概率分布函数：概率分布概念解完之后，自然就到概率分布函数了

看看下图课本中定义的分布律和累积概率函数：其中分布律又是一个不统一叫法的丑恶典型！这里的分布律明明就是我们刚刚讲的“概率函数”，完全就是一个东西嘛！但是我知道很多教材就是叫分布律的；

上图公式中分布律其实就是我们（1）中的概率函数，F(x)就代表概率分布函数啦。发现F(x)是一个概率函数的累加；发现概率分布函数的秘密了吗？它其实根本不是个新事物，它就是概率函数取值的累加结果！所以它又叫累积概率函数！

其实，我觉得叫它累积概率函数还更好理解！！概率函数和概率分布函数就是描述概率的两个不同的手段；

3、连续型随机变量也有"概率函数"和"概率分布函数"吗？

有！连续型随机变量也有它的“概率函数”和“概率分布函数”，但是连续型随机变量的“概率函数”换了一个名字，叫做“概率密度函数”！为啥要这么叫呢？我们还是借用大师的话来告诉你，在陈希孺老师所著的《概率论与数理统计》这本书中

如果这么解析你还是不太懂的话，看看下面的这个公式：

概率密度函数用数学公式表示就是一个定积分的函数，定积分在数学中是用来求面积的，而在这里，你就把概率表示为面积即可！

左边是F(x)连续型随机变量分布函数画出的图形，右边是f(x)连续型随机变量的概率密度函数画出的图像，它们之间的关系就是，概率密度函数是分布函数的导函数。

两张图一对比，你就会发现，如果用右图中的面积来表示概率，利用图形就能很清楚的看出，哪些取值的概率更大！这样看起来是不是特别直观，特别爽！！所以，我们在表示连续型随机变量的概率时，用f(x)概率密度函数来表示，是非常好的！密度函数曲线越高，也就代表着这个区间的概率越密集。

二、正态分布

大学记忆中谈到正态分布（也叫高斯分布）第一反应就是中心对称的凸起的曲线(中间密集、两边稀疏)，现实生活中很多东西都符合正态分布(正常人群的身高、体重、考试成绩、家庭收入等等)，除此外理解很少了；直到最近重新回炉看书，才慢慢体会到概率隐藏的很多秘密；彻底弄懂正态分布是灵活运用统计学中各种假设检验方法、看懂p值，理解均数置信区间的前提。

1、从产生历史&名词定义说起

先看看正态分布的产生历史&大学课本中的定义：维多利亚时期的学者Francis Gallton对数据分布很着迷，他制造了一台可以产生数据分布的装置，他发现这种形状适用于很多数据，他将其命名为"正态分布"（The Normal Distribution）.

先不用纠结正态分布概率密度函数的复杂积分公式，我们后续会逐层深入；服从正态分布意味着大部分人的身高都会在人群的平均身高上下波动，特别矮和特别高的都比较少见。为什么此类分布符合中间密集、两边稀疏的正态分布特征？

这其实与同质与变异的概念相关（参见 统计学核心思维与统计描述）。因为我们研究的对象具有同质性（比如都是成年的中国男子），所以其特征往往是趋同的，即存在一个基准；但由于个体变异的存在（当然变异不会太大），这些特征又不是完全一致，所以会以一定的幅度在基准的上下波动，从而形成了中间密集，两侧稀疏的特征。

2、 连续型随机变量研究区间概率

首先，正态分布属于“连续型随机变量分布”的一类。我们知道，对于连续型随机变量，我们不关注“点概率”，只关注“区间概率”，这是什么意思？

我们看这个例子，假定随机变量X指是“北京市成年男子的身高”，理论上它可以取任意正数，所以我们把它当做一个连续型随机变量（连续型变量，就是指可以取某一区间或整个实数轴上的任意一个值的变量）来看待。这里，我们先想一想如何计算P(X =1.87)? 即身高恰好完全exactly等于1.87的概率是多少，这就是所谓的“点概率”。更极端一点，让随机变量Y是[0,1]这个区间上的任意一点，那么Y的取值有多少个呢？无数多个，我们数不清楚，所以Y 取某一个具体的值的概率是1除以无数，即可以看做是0。于是，这里透露一个很重要的结论：连续型随机变量取任意某个确定的值的概率均为0。因此，对于连续型随机变量，我们通常不研究它取某个特定值的概率，而研究它在某一段区间上的取值，比如身高在1.70～1.80的概率。

3、均数&标准差

前面说对于正态分布的概率密度函数以及积分不用特别关注，那真正需要关注的是什么呢？就是均数和标准差。这里需要明确的是，一旦谈及正态分布，我们首先要想到它的两个参数：均数是多少和标准差是几。每次一遇到正态分布就迅速找这两个概念，最好形成条件反射，因为这两个数才是我们日后运用正态分布解决实际问题的"利器"。

关于正态分布均数和标准差的性质，我们这里简单总结一下：

• 概率密度曲线在均值处达到最大，并且对称
• 一旦均值和标准差确定，正态分布曲线也确定；
• 当X的取值向横轴左右两个方向无限延伸时，理论上永远不会与之相交
• 正态随机变量在特定区间上的取值概率由正态曲线下的面积给出，而且曲线下的总面积等于1；
• 均值可取实数轴上的任意，决定正态曲线的具体位置；标准差决定曲线的"陡峭"或者"扁平"程度：标准差越大，正态曲线越扁平；标准差越小，意味着大多数变量值距离均数距离越短，因此大多数数值都紧密的聚集在均数周围，图形所能覆盖的变量值就少些（比如1+0.1，1-0.1涵盖[0.9，1.1]），于是都挤在一块，图形上呈现瘦高型。相反标准差越大，数据跨度就比较大，分散程度大，所覆盖变量值就越多（比如1+0.5，1-0.5覆盖[0.5,1.5]）,图形呈现"矮胖型"。

我们可以对照下图直观地看一下，图中黄色曲线为A，蓝色曲线为B，紫红色曲线为C。如图，我们可以看到均数的大小决定了曲线的位置，标准差的大小决定了曲线的胖瘦。A和B的均值一样，但标准差不同，所以形状不同，根据我们的描述，图形越瘦高，标准差越小，图形越扁平，标准差越大。确实如此，图中B的标准差是1/2，小于A的标准差1。

4、标准化&查表求概率

接下来，我们通过一个例子来看如何通过查表法计算正态分布变量在某个区间的概率。首先，我们看这个问题，说小明每天上学的通勤时间是一个随机变量X，这个变量服从正态分布。统计他过去20天的通勤时间（单位：分钟）：26、33、65、28、34、55、25、44、50、36、26、37、43、62、35、38、45、32、28、34。现在我们想知道他上学花30~45分钟的概率。

首先，我们将问题转化为数学表达式，要算他上学花30~45分钟的概率，就是求P（30 < X < 45）。之前我们一直强调，一个变量服从正态分布，就要立马考虑到它的均数和标准差是多少。这里我们简化一下用他过去20天的样本数据来代替。所以，我们首先计算这20天通勤时间的样本均数及标准差，分别为38.8（分钟）和11.4（分钟）。

然后，我们进行标准化，这一步很重要，也称z变换。通过标准化，所有服从一般正态分布的随机变量都变成了服从均数为0，标准差为1的标准正态分布。对于服从标准正态分布的随机变量，专门用z表示。因此，求P（30 < X < 45），就转换成了求P（-0.77 < Z < 0.54），标准化的具体计算为：

1. 30 → （30-38.8）/ 11.4 = - 0.77
2. 45 → （45-38.8）/ 11.4 = 0.54
3. X → Z
4. P（30 ≤ X ≤ 45）= P （-0.77 ≤ Z ≤ 0.54）

这里简单提醒一下，经过标准化后，原来的曲线的形状不会变化，即不会改变胖瘦，只是位置发生平移，比如下图中的例子，经过标准化实际上只是均数从1010移到了0。

完成z变换，我们就通过可以利用z值表找到对应的概率值。下图就是z值表，一般的统计教科书后面都有，同学们也可以在网上查到。

再三强调，图中阴影部分的面积代表的是Z ≤ z的概率（重要的话讲三遍，注意是“≤”）。另外，还有两个根据定义成立的两个公式：

• 一是P（Z ≥ z）= 1- P（Z ≤ z）；
• 二是P（Z≤-z）= 1-P（Z ≤ z）大家也需要了解。

下面我们正式看看怎么查表，前面我们已经把问题转化成求P (-0.77 ≤ Z ≤0.54) = P (Z ≤ 0.54)–P (Z ≤ -0.77)，于是，我们需要找当Z≤0.54和Z≤-0.77的概率值然后相减即可。

先看Z≤0.54的P值，对照下图，首先看表格最左边那一列，找到0.5，然后，因为0.54的第二位小数是4，所以定位到顶行找到“4”那一列，得到0.7054；同样的方法，我们找到Z≤-0.77对应的P值0.2206。最后我们就能算出，P (-0.77 ≤ Z ≤0.54) = 0.4848，约等于0.5。因此，我们可以说，小明上学通勤时间花费30~45分钟的概率是50%，这个概率还挺大的，占了一半。我们通过这个具体的例子详细讲解了随机变量在某个区间的概率求解，不是因为这个计算有多重要，而是想提前给你打好基础，方便理解假设检验及p值等相关概念。

5、三个百分数：68%，95%，99.7%

熟悉了Z变换、查表求概率，我们来看看正态分布运用十分广泛的三个百分数：68%，95%，99.7%。先看标准正态分布，我们知道一个变量服从标准正态分布，它的均数是0，标准差是1，那除了这两个数字之外，我们还能获得更多的信息吗？可以，这三个百分数告诉了我们答案。看下面这3个图：

虽然理论上正态随机变量可以取无数个值，定义域是整个实数轴，但实际上在[-1，1]这个区间就包含了它可以取的68%的值，[-2，2]区间包含了95%的值，[-3，3]包含了它可能取的99.7%的值。这里的1，2，3分别代表一个、两个和三个标准差（标准正态分布的均数为0，标准差为1）。所以，根据这些，我们就可以推断，一个服从标准正态分布的变量，它的取值很不可能超过2，极不可能超过3。这个用处非常大，一下子把我们要研究的重心从整个实数轴缩小到[-3，3]这个区间。另外，这里虽然是以标准正态分布为例进行说明，但这个性质是完全可以推到普通的正态分布的变量的。百分数不变，不过均数和标准差不再是0和1，而是代入具体分布的均数和标准差即可。下面我们来看一个实际应用的例子。

某小学学生身高的平均值和标准差分别为1.4（米）和0.15（米），我们知道身高一般是服从正态分布的，由此我们可以知道这个学校有68%的学生的身高在1.25到1.55，这里的1.25和1.55就是1.4加减0.15得到的（均数加减一个标准差），有95%的学生身高在1.1到1.7之间（均数加减两个标准差），由此便极大地提升了我们对数据的掌握程度。讲完这些你会发现一种巧妙的求解均数和标准差的方法：如果我们知道了某个变量的95%区间的取值（关于均值对称），我们就可以算出对应的均数和标准差，进而几乎知道了一切。

三、正态分布应用（机器学习、量化分析方向）

//todo

如何使用 Python 探索变量的概率分布？

//todo