逐步回归法的基本步骤_多重线性回归方法之前进法

前进法简介

前进法是决定备选自变量取舍的又一种回归分析方法,其基本思路与逐步回归法相类似,具体做法是:向前选择过程从模型中自变量个数为零开始,第一个被纳入模型中的是与因变量有绝对值为最大的相关系数,且符合“纳入标准”的自变量。下一个将被纳入模型中的自变量,应该是在剩余的备选变量中偏相关系数的绝对值为最大,且符合“纳人标准”的自变量。这种叠代过程一直进行下去,直到再也没有备选自变量符合“纳人标准”为止。

实验数据

现有一份学生身体测试数据集。将学生的身高、体重、胸围作为自变量来对因变量肺呼量进行多重线性回归拟合。来学习本文的重点：多重线性回归前进法。选择「分析」-「回归」-「线性」。方法选择前进。

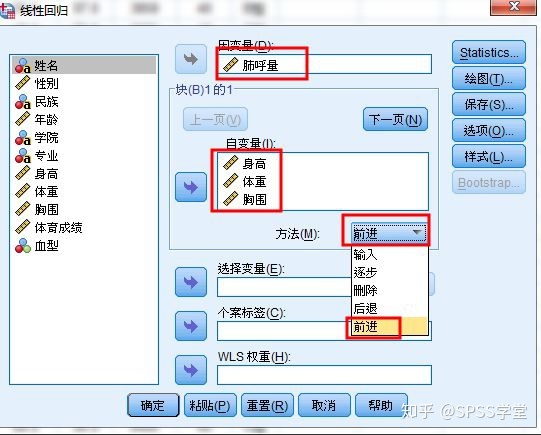
实验结果解读

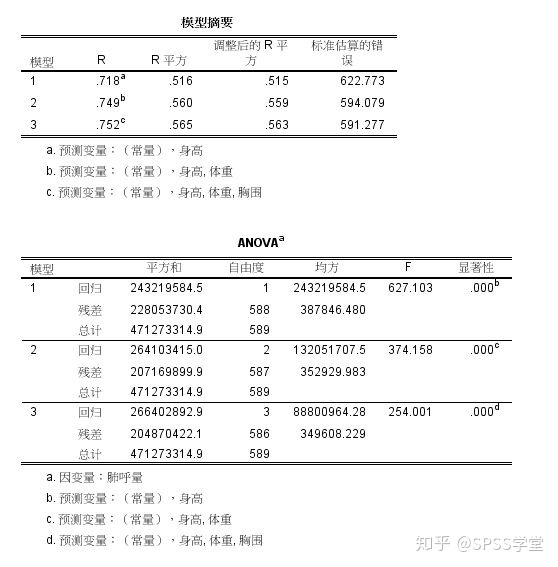
根据前进法，模型1首先纳入方程的预测变量是身高。模型2纳入方程的预测变量中加入了体重自变量，所以有两个预测变量。模型3纳入方程的预测变量在模型2基础上新加了胸围自变量。所以有三个预测变量。

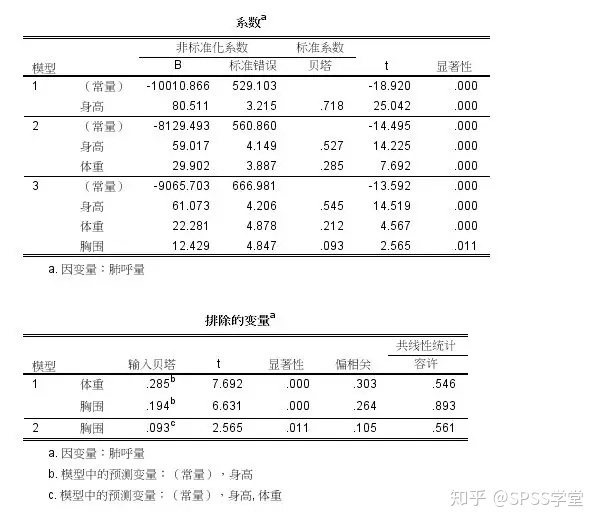
从排除的变量表格中中偏相关系数也可以看出预测变量依次进入方程的顺序。根据前进法，模型1首先纳入方程的预测变量是身高。排除的变量是体重和胸围。模型2在模型1的基础上纳入了体重而排除了胸围自变量。是因为体重偏相关系数=0.303>胸围偏相关系数=0.264.模型3纳入方程的预测变量在模型2基础上新加了胸围自变量。是因为胸围变量的显著性<0.05.具有统计学意义，所以模型3有三个预测变量。最后我们建立了3个有统计学意义的多元线性回归拟合模型，根据统计学学上R^2最大最优原则，选择了模型3。

在SPSS学堂中，回复20180612，可获得本次案例数据哦~