
 为:( )
为:( )
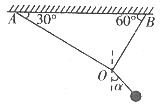 图1
A. 15°
B. 30°
C. 45°
D. 60°
解析:对O点进行受力分析,O点受到OA绳和OB绳的拉力FA和FB及小球通过绳子对O点的拉力F三个力的作用,在这三个力的作用下O点处于平衡状态,由“等值、反向”原理得,FA和FB的合力F合与F是等值反向的,由平行四边形定则,作出FA和FB的合力F合,如图2所示,由图可知
图1
A. 15°
B. 30°
C. 45°
D. 60°
解析:对O点进行受力分析,O点受到OA绳和OB绳的拉力FA和FB及小球通过绳子对O点的拉力F三个力的作用,在这三个力的作用下O点处于平衡状态,由“等值、反向”原理得,FA和FB的合力F合与F是等值反向的,由平行四边形定则,作出FA和FB的合力F合,如图2所示,由图可知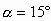 ,故答案是A。
,故答案是A。
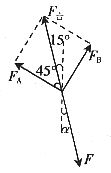 图2
(2)矢量三角形法:物体受同一平面内三个互不平行的力作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形;反之,若三个力矢量箭头首尾相接恰好构成三角形,则这三个力的合成必为零,因此可利用三角形法,求得未知力。
例2. 图3中重物的质量为m,轻细线AO和BO的A、B端是固定的。平衡时AO是水平的,BO与水平面的夹角为
图2
(2)矢量三角形法:物体受同一平面内三个互不平行的力作用平衡时,这三个力的矢量箭头首尾相接,构成一个矢量三角形;反之,若三个力矢量箭头首尾相接恰好构成三角形,则这三个力的合成必为零,因此可利用三角形法,求得未知力。
例2. 图3中重物的质量为m,轻细线AO和BO的A、B端是固定的。平衡时AO是水平的,BO与水平面的夹角为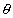 。AO的拉力
。AO的拉力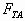 和BO的拉力
和BO的拉力 的大小是:( )
的大小是:( )
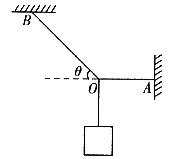 图3
A.
图3
A. 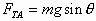 B.
B. 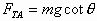 C.
C. 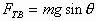 D.
D. 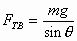 解析:因结点O受三力作用而平衡,且
解析:因结点O受三力作用而平衡,且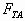 与mg垂直,所以三力应组成一个封闭的直角三角形,如图4所示,由直角三角形知识得:
与mg垂直,所以三力应组成一个封闭的直角三角形,如图4所示,由直角三角形知识得: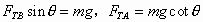 ,所以选项B、D正确。
,所以选项B、D正确。
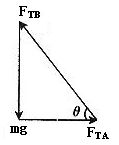 图4
(3)正弦定理法:三力平衡时,三个力可构成一封闭三角形,若由题设条件寻找到角度关系,则可用正弦定理列式求解。
例3. 如图5(a)所示,质量为m的物体用一轻绳挂在水平轻杆BC的C端,B端用铰链连接,C点由轻绳AC系住,已知AC、BC夹角为
图4
(3)正弦定理法:三力平衡时,三个力可构成一封闭三角形,若由题设条件寻找到角度关系,则可用正弦定理列式求解。
例3. 如图5(a)所示,质量为m的物体用一轻绳挂在水平轻杆BC的C端,B端用铰链连接,C点由轻绳AC系住,已知AC、BC夹角为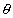 ,则轻绳AC上的张力和轻杆BC上的压力大小分别为多少?
,则轻绳AC上的张力和轻杆BC上的压力大小分别为多少?
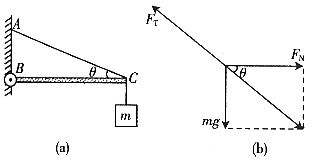 图5
解析:选C点为研究对象,受力情况如图5(b)所示,由平衡条件和正弦定理可得
图5
解析:选C点为研究对象,受力情况如图5(b)所示,由平衡条件和正弦定理可得
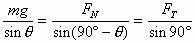 即得
即得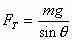 和
和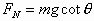 所以由牛顿第三定律知,轻绳AC上的张力大小为
所以由牛顿第三定律知,轻绳AC上的张力大小为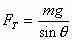 ,轻杆BC上的压力大小为
,轻杆BC上的压力大小为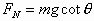 。
(4)三力汇交原理:如果一个物体受到三个不平行外力的作用而平衡,这三个力的作用线必在同一平面上,而且必为共点力。
例4. 如图6所示,两光滑板AO、BO与水平面夹角都是60°,一轻质细杆水平放在其间,用竖直向下的力F作用在轻杆中间,杆对两板的压力大小为____________。
。
(4)三力汇交原理:如果一个物体受到三个不平行外力的作用而平衡,这三个力的作用线必在同一平面上,而且必为共点力。
例4. 如图6所示,两光滑板AO、BO与水平面夹角都是60°,一轻质细杆水平放在其间,用竖直向下的力F作用在轻杆中间,杆对两板的压力大小为____________。
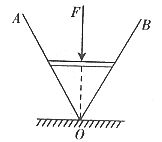 图6
解析:选轻杆为研究对象,其受三个力而平衡,因此这三力必为共点力(汇交于O”),作出受力分析如图7所示。
图6
解析:选轻杆为研究对象,其受三个力而平衡,因此这三力必为共点力(汇交于O”),作出受力分析如图7所示。
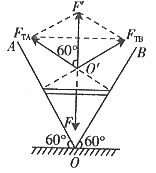 图7
由图可知,FTA与FTB对称分布,所以
图7
由图可知,FTA与FTB对称分布,所以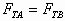 ,且这两力的夹角为120°,其合力F”应与F相等,以FTA,FTB为邻边构成的平行四边形为菱形,其性质为对角线垂直且平分,根据三角形知识,有
,且这两力的夹角为120°,其合力F”应与F相等,以FTA,FTB为邻边构成的平行四边形为菱形,其性质为对角线垂直且平分,根据三角形知识,有
 又因为
又因为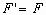 所以
所以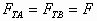 2. 解多个共点力作用下物体平衡问题的方法
多个共点力作用下物体的平衡问题,常采用正交分解法。可将各力分别分解到x轴上和y轴上,运用两坐标轴上的合力等于零的条件,即
2. 解多个共点力作用下物体平衡问题的方法
多个共点力作用下物体的平衡问题,常采用正交分解法。可将各力分别分解到x轴上和y轴上,运用两坐标轴上的合力等于零的条件,即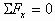 、
、 求解。值得注意的是,对x、y方向选择时,要尽可能使落在x、y轴上的力多,且被分解的力尽可能是已知力,不宜分解待求力。
例5. 在机械设计中亦常用到下面的力学原理,如图8所示,只要使连杆AB与滑块m所在平面间的夹角
求解。值得注意的是,对x、y方向选择时,要尽可能使落在x、y轴上的力多,且被分解的力尽可能是已知力,不宜分解待求力。
例5. 在机械设计中亦常用到下面的力学原理,如图8所示,只要使连杆AB与滑块m所在平面间的夹角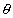 大于某个值,那么,无论连杆AB对滑块施加多大的作用力,都不可能使之滑动,且连杆AB对滑块施加的作用力越大,滑块就越稳定,工程力学上称之为“自锁”现象。为使滑块能“自锁”,
大于某个值,那么,无论连杆AB对滑块施加多大的作用力,都不可能使之滑动,且连杆AB对滑块施加的作用力越大,滑块就越稳定,工程力学上称之为“自锁”现象。为使滑块能“自锁”,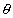 应满足什么条件?(设滑块与所在平面间的动摩擦因数为
应满足什么条件?(设滑块与所在平面间的动摩擦因数为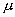 )
)
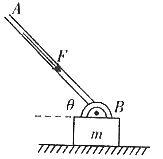 图8
解析:滑块m的受力分析如图9所示,将力F分别在水平和竖直两个方向分解,则:
图8
解析:滑块m的受力分析如图9所示,将力F分别在水平和竖直两个方向分解,则:
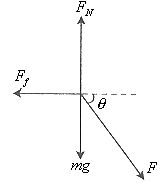 图9
在竖直方向上
图9
在竖直方向上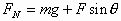 在水平方向上
在水平方向上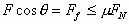 由以上两式得
由以上两式得

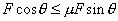 故
故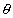 应满足的条件为
应满足的条件为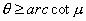 3. 研究对象的灵活选择–整体法与隔离法
用整体法还是用隔离法,其实质就是如何合理选取研究对象,使受力分析和解题过程简化。对一个较为复杂的问题,两者应灵活选用、有机结合,才能到达迅速求解的目的。
例6. 在粗糙水平面上有一个三角形的木块,在它的两个粗糙斜面上分别放有两个质量m1和m2的小木块,
3. 研究对象的灵活选择–整体法与隔离法
用整体法还是用隔离法,其实质就是如何合理选取研究对象,使受力分析和解题过程简化。对一个较为复杂的问题,两者应灵活选用、有机结合,才能到达迅速求解的目的。
例6. 在粗糙水平面上有一个三角形的木块,在它的两个粗糙斜面上分别放有两个质量m1和m2的小木块,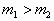 ,如图10所示,已知三角形木块和两个小木块都是静止的,则粗糙水平面对三角形木块( )
,如图10所示,已知三角形木块和两个小木块都是静止的,则粗糙水平面对三角形木块( )
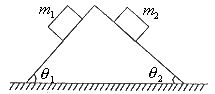 图10
A. 有摩擦力的作用,摩擦力的方向水平向右;
B. 有摩擦力的作用,摩擦力的方向水平向左;
C. 有摩擦力的作用,但摩擦力的方向不能确定,因m1、m2和
图10
A. 有摩擦力的作用,摩擦力的方向水平向右;
B. 有摩擦力的作用,摩擦力的方向水平向左;
C. 有摩擦力的作用,但摩擦力的方向不能确定,因m1、m2和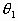 、
、 的数值并未给出;
D. 以上结论都不对。
解析:因为三角形木块和两个小木块都静止,所以可将三者看成一个整体如图11所示,其在竖直方向受重力和水平面的支持力,合力为零。在水平方向没有受其他力的作用,所以整体在水平方向上没有相对水平面的运动趋势,因此粗糙水平面对三角形木块没有静摩擦力。
的数值并未给出;
D. 以上结论都不对。
解析:因为三角形木块和两个小木块都静止,所以可将三者看成一个整体如图11所示,其在竖直方向受重力和水平面的支持力,合力为零。在水平方向没有受其他力的作用,所以整体在水平方向上没有相对水平面的运动趋势,因此粗糙水平面对三角形木块没有静摩擦力。
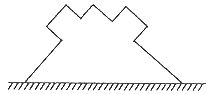 图11
例7. 如图12所示,两块相同的竖直木板之间有质量均为m的四块相同的砖,用两个大小为F的水平压力压木板,使砖块静止不动。设所有接触面均粗糙,则第3块砖对第2块砖的摩擦力为( )
图11
例7. 如图12所示,两块相同的竖直木板之间有质量均为m的四块相同的砖,用两个大小为F的水平压力压木板,使砖块静止不动。设所有接触面均粗糙,则第3块砖对第2块砖的摩擦力为( )
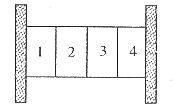 图12
A. 0
B.
图12
A. 0
B. 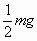 C. mg
D. 2mg
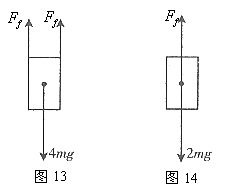
解析:将4块砖为整体进行受力分析如图13所示,可知两侧木板对砖的静摩擦力均为竖直向上,且大小为2mg;再把第1、2两块砖为整体进行受力分析如图14所示,由图可知木板对砖的静摩擦力与砖的重力2mg是一对平衡力,这表明第3块与第2块砖之间没有静摩擦力。所以选项A正确。
C. mg
D. 2mg
解析:将4块砖为整体进行受力分析如图13所示,可知两侧木板对砖的静摩擦力均为竖直向上,且大小为2mg;再把第1、2两块砖为整体进行受力分析如图14所示,由图可知木板对砖的静摩擦力与砖的重力2mg是一对平衡力,这表明第3块与第2块砖之间没有静摩擦力。所以选项A正确。
 4. 求共点力作用下物体平衡的极值问题的方法
共点力作用下物体平衡的极值问题是指研究平衡问题中某个力变化时出现的最大值或最小值,处理这类问题常用解析法和图解法。
例8. 如图15所示,物体的质量为2kg,两根轻细绳AB和AC的一端连接于竖直墙上,另一端系于物体上,且AC绳水平时,两绳所成角为
4. 求共点力作用下物体平衡的极值问题的方法
共点力作用下物体平衡的极值问题是指研究平衡问题中某个力变化时出现的最大值或最小值,处理这类问题常用解析法和图解法。
例8. 如图15所示,物体的质量为2kg,两根轻细绳AB和AC的一端连接于竖直墙上,另一端系于物体上,且AC绳水平时,两绳所成角为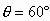 。在物体上另施加一个方向与水平线成
。在物体上另施加一个方向与水平线成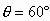 的拉力F,若要使绳都能伸直,求拉力F的大小范围。
的拉力F,若要使绳都能伸直,求拉力F的大小范围。
 图15
解析:作出A受力示意图,并建立直角坐标如图16所示,由平衡条件有:
图15
解析:作出A受力示意图,并建立直角坐标如图16所示,由平衡条件有:
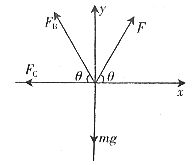 图16
图16
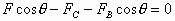
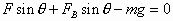 由以上两式得
由以上两式得
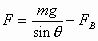 ①
及
①
及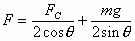 ②
要使两绳都能绷直,需有
②
要使两绳都能绷直,需有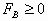 ③
③
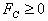 ④
由①③两式得F有最大值
④
由①③两式得F有最大值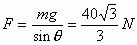 由②④两式得F有最小值
由②④两式得F有最小值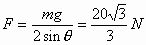 综合得F的取值范围为
综合得F的取值范围为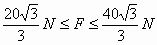 例9. 重量为G的木块与水平地面间的动摩擦因数为
例9. 重量为G的木块与水平地面间的动摩擦因数为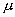 ,一人欲用最小的作用力F使木块做匀速运动,则此最小作用力的大小和方向应如何?
解析:由于
,一人欲用最小的作用力F使木块做匀速运动,则此最小作用力的大小和方向应如何?
解析:由于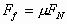 ,所以不论FN如何改变,
,所以不论FN如何改变,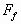 与FN的合力F1的方向都不会发生变化,如图17(甲)所示,合力F1与竖直方向的夹角一定为
与FN的合力F1的方向都不会发生变化,如图17(甲)所示,合力F1与竖直方向的夹角一定为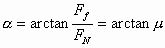 。
由木块做匀速运动可知F、F1和G三力平衡,且构成一个封闭三角形,当改变F的方向时,F和F1的大小都会发生改变,由图17(乙)知,当F和F1的方向垂直时F最小。故由图中几何关系得
。
由木块做匀速运动可知F、F1和G三力平衡,且构成一个封闭三角形,当改变F的方向时,F和F1的大小都会发生改变,由图17(乙)知,当F和F1的方向垂直时F最小。故由图中几何关系得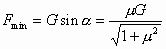 。
。
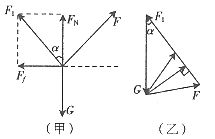 图17
5. 共点力平衡问题中的“变”与“不变”
物体在共点力作用下处于平衡状态时,即使在一些量变的过程中某些本质并不变。因此寻找变化中保持不变的部分,乃是解决平衡问题的一种重要方法。
例10. 三个相同的支座上分别搁着三个质量和直径都相等的光滑圆球a、b、c,支点P、Q在同一水平面上,a球的重心
图17
5. 共点力平衡问题中的“变”与“不变”
物体在共点力作用下处于平衡状态时,即使在一些量变的过程中某些本质并不变。因此寻找变化中保持不变的部分,乃是解决平衡问题的一种重要方法。
例10. 三个相同的支座上分别搁着三个质量和直径都相等的光滑圆球a、b、c,支点P、Q在同一水平面上,a球的重心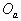 位于球心,b球和c球的重心
位于球心,b球和c球的重心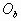 、
、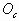 分别位于球心的正上方和球心的正下方,如图18所示,三球均处于平衡状态,支点P对a球的弹力为
分别位于球心的正上方和球心的正下方,如图18所示,三球均处于平衡状态,支点P对a球的弹力为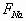 ,对b球和c球的弹力分别为
,对b球和c球的弹力分别为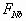 、
、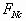 ,则( )
,则( )
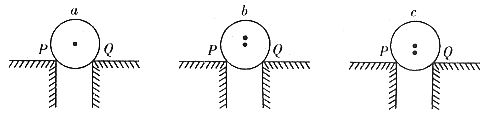 图18
A.
图18
A. 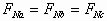 B.
B. 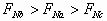 C.
C. 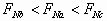 D.
D. 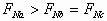 解析:本题的干扰因素是三个球的重心在竖直方向的位置发生了变化(a在球心、b在球心之上、c在球心之下)。但是三个球的质量和直径都相等,重力方向均竖直向下,而且支点的支持力方向也完全相同,所以它们受力情况完全相同,支持力大小也必然相同,所以选项A正确。
评析:在变化中求不变的思想是最普遍的物理思想,本题中圆球重心的高度虽然发生了变化,但问题的本质–圆球的受力情况并不变化,所以支点P对三球的弹力应相同。
解析:本题的干扰因素是三个球的重心在竖直方向的位置发生了变化(a在球心、b在球心之上、c在球心之下)。但是三个球的质量和直径都相等,重力方向均竖直向下,而且支点的支持力方向也完全相同,所以它们受力情况完全相同,支持力大小也必然相同,所以选项A正确。
评析:在变化中求不变的思想是最普遍的物理思想,本题中圆球重心的高度虽然发生了变化,但问题的本质–圆球的受力情况并不变化,所以支点P对三球的弹力应相同。

扫一扫关注我们,
更多咨询早知道!
学好高中物理也不是想象的那么难,看看下面的模型你是否熟悉?
模型1 运动图像的区别与联系模型2 运动图像的分析与运用模型3 匀变速直线运动规律的灵活选用模型4 追及和相遇问题的分析模型5 自由落体运动和竖直上抛运动的分析模型6 杆上弹力方向的分析模型7 绳上死结和活结问题的分析模型8 摩擦力的分析与计算模型9 对物体进行受力分析的方法模型10 力的矢量三角形的灵活应用模型11 整体法和隔离法在多物体平衡问题中的运用模型12 牛顿第二定律的瞬时问题的分析模型13 与牛顿第二定律相关的临界问题的分析模型14 与超重、失重相关联的问题的分析模型15 牛顿运动定律中的图像问题的分析模型16 整体法和隔离法在连接体类问题中的运用模型17 牛顿运动定律在滑块—滑板类问题中的运用模型18 牛顿运动定律在传送带类问题中的运用模型19 小船渡河类问题的分析与求解模型20 绳或杆相关联物体运动的合成与分解模型21 平抛运动规律的综合应用模型22 圆锥摆模型问题的分析模型23 类圆锥摆模型的分析模型24 轻绳或内轨道模型在竖直平面内圆周运动的临界问题模型25 轻杆或管模型在竖直平面内圆周运动的临界问题模型26 水平面内圆周运动的临界问题模型27 天体质量和密度的估算模型28 卫星稳定运行中线速度v、角速度ω、周期T和加速度a与轨道半径r的关系模型29 卫星的变轨问题模型30 人造卫星和宇宙速度模型31 万有引力定律和其他运动规律的综合应用模型32 双星问题的分析模型33 三星(质量相等)问题的分析模型34 机车启动问题的讨论——以恒定功率启动模型35 机车启动问题的讨论——以恒定加速度启动模型36 变力做功的计算模型37 动能定理在多过程问题中的运用模型38 对机械能守恒定律的理解模型39 对机械能守恒定律的应用模型40 动能定理与机械能守恒定律的比较与运用模型41 对功能关系的理解模型42 传送带模型中的能量问题模型43 碰撞结果可能性问题的分析模型44 动量守恒在子弹打木块模型中的应用模型45 动量守恒在“人船模型”(反冲问题)中的应用模型46 动量守恒在弹簧类问题中的运用模型47 动量守恒在多体多过程问题中的运用
模型48 电场线和等势面的特点模型49 对电场性质的理解与应用模型50 带电粒子在匀强电场中做直线运动问题的分析模型51 带电粒子在匀强电场中偏转问题的分析模型52 带电粒子在电场中做其他运动问题的分析模型53 电容器充电后断开电源类问题的分析模型54 电容器充电后始终与电源相连类问题的分析模型55 电路动态问题的分析模型56 与电功、电功率、电热相关的问题的综合分析模型57 含容电路问题的综合分析模型58 伏安特性曲线的理解与运用模型59 安培力作用下导体在磁场中运动问题的分析模型60 安培力作用下通电导体平衡与加速问题的分析模型61 带电粒子在磁场中的运动情况分析模型62 画轨迹、定圆心、求半径、求时间模型63 带电粒子在有界磁场中运动的临界问题模型64 带电粒子在磁场中运动的多解问题分析模型65 带电粒子在含磁场的组合场中运动问题的分析模型66 带电粒子在含磁场的叠加场中运动情况的分析模型67 带电粒子在含磁场的叠加场中运动时粒子重力问题模型68 对楞次定律的理解与应用模型69 对法拉第电磁感应定律的理解与应用模型70 电磁感应中图像问题的分析模型71 电磁感应中电路问题的分析模型72 电磁感应中力学问题的综合分析模型73 交变电流的产生与表达模型74 交流电“四值”的理解及运用模型75 变压器的分析与计算——基本规律模型76 变压器的分析与计算——动态问题分析模型77 输电电路的基本分析模型78 远距离高压输电问题的分析
模型79 秒表的使用与读数模型80 游标卡尺的使用与读数模型81 螺旋测微器的使用与读数模型82 打点计时器的使用模型83 电流表、电压表的使用与读数模型84 多用电表的使用与读数模型85 传感器的简单使用模型86 研究匀变速直线运动模型87 探究弹力与弹簧伸长的关系模型88 验证力的平行四边形定则模型89 验证牛顿运动定律模型90 探究动能定理模型91 验证机械能守恒定律模型92 力学经典演示实验模型93 伏安法测电阻的电路设计模型94 测定金属的电阻率模型95 描绘小电珠的伏安特性曲线模型96 测定电源的电动势和内阻模型97 实验原理的迁移设计模型98 实验方案的创新设计模型99 实验方法的迁移设计模型100 数据处理的迁移设计

扫一扫关注我们,
更多咨询早知道!
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








