算法证明_CFR+算法证明过程

在介绍CFR+算法之前，我们首先介绍一下基础概念。

在CFR+算法中，counterfactual utility被定义为以下形式：

然后在regret的基础上，CFR+算法定义了一个regretlike value，注意在这里CFR+算法的regret为一个累加值，而CFR算法定义的regret为平均值，需要乘以1t：

,where

另外，在CFR+算法中，最后输出的平均策略为以下形式：

然后CFR+算法的bound为：

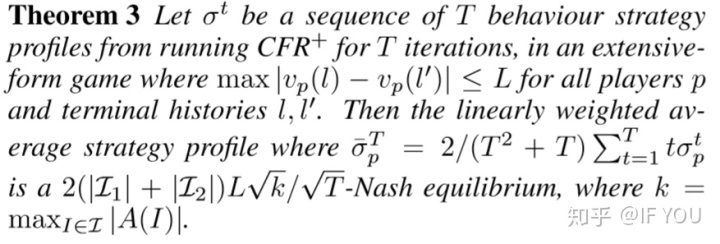
bound证明

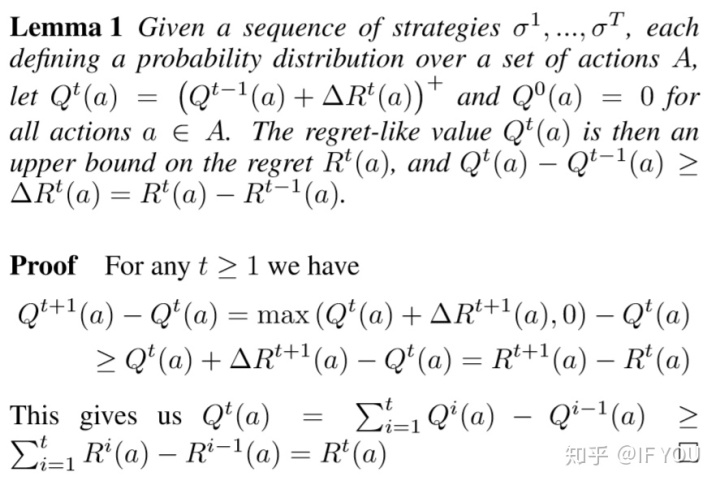
在对Lemma 1的证明过程中，我们可以得出以下结论：

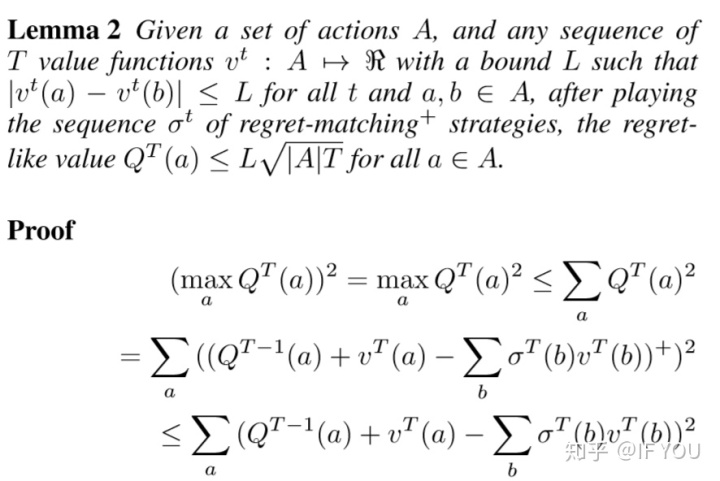
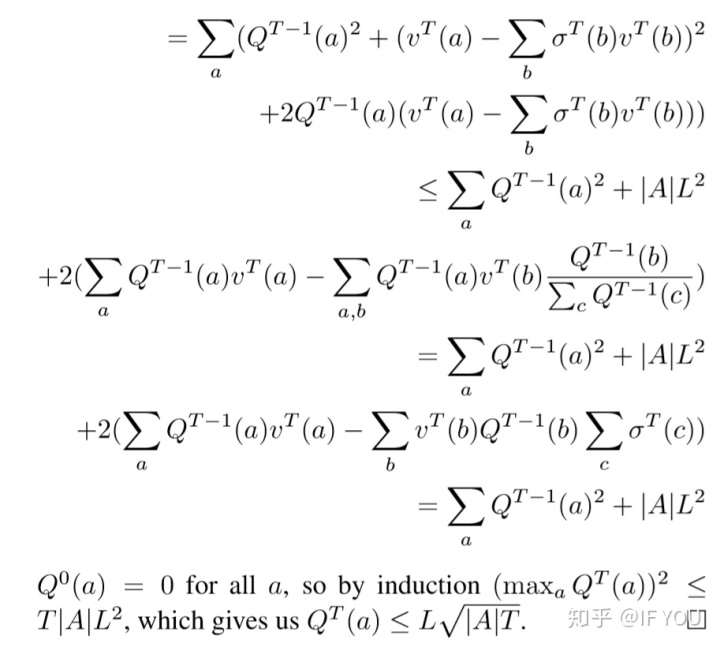
我们得到了

，之后我们可以从Lemma 1可知

，于是，我们得出以下结论：

然后我们引入Lemma 3， Lemma 3很容易证明，可以直接看出：

然后证明Lemma 4：

Lemma 4的证明就是将原有的序列扩充为1，2，3，。。。，T，这样的话等于有（T^2+T）/2的过程，然后我们再引入Lemma 3，这样的就可以求出新的bound：

然后我们由CFR算法的定义可知

于是可以得到新的

结论

从CFR算法和CFR+算法的证明过程中我们可以获取以下证明过程范式。

首先定义average overall regret：

因为直接优化average overall regret困难，然后我们定义immediate counterfactual regret，并且最优化他，但是优化这个困难，于是我们优化他的拟合项counterfactual regret，使其小于

，就可以得到

。记住这样的话，counterfactual regret必须除t作为一个平均值，而CFR+算法直接将其作为了累加项。

在CFR+算法中，我们的counterfactual regret没有除t。但是我们得到了一个结论：

然后我们计算累加的counterfactual regret：

为了求出上面公式的bound，我们一般需要Lemma 3，而在LCFR中，需要在Lemma 3的基础上进行进一步的扩展。

然后我们证明

，于是得到

。