泰勒公式推导过程_浅谈泰勒展开的巧记及其唯一性的妙用（1）

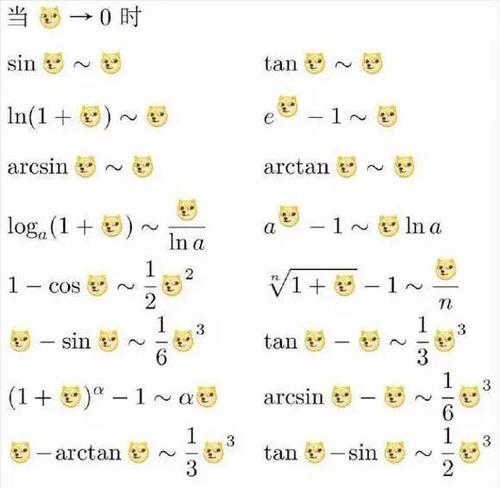
本文全部内容均转载自作者的公众号【数理tricks】

生活不可万事都硬刚，学术也一样~

在物理学习中常用到泰勒展开做局域的近似计算或直接作为考察某些物理过程的研究方法（正如热学中可逆过程既可作为真实过程的近似，又是一些热学过程的研究手段），正因如此，泰勒展开在物理学研究中占有重要的地位，而若按照正常的算法，泰勒展开公式要做若干次求导运算，在绝大多数时候显得极其繁琐，此时我们便会想找一些更便捷的方法去记忆或以极短的时间迅速算出一些常用函数的泰勒级数。

上篇主要罗列几种记忆技巧，并揭示不同知识点之间的一些内在联系，下面的每一章内容都不止是一道题，更是一种思维方法，请用心体会。

第一章、从函数本身性质（图像）去记忆：

我们下面以正弦与余弦函数的麦克劳林级数为例：

首先强调一个观点，泰勒展开从某种角度上可以说是在“局域模拟”原函数，对于正弦函数而言，其本身是一个奇函数，而要将奇函数用一个无限项的多项式去模拟，这个多项式的每一项必然均为奇函数，因此在正弦函数的泰勒展开式中没有偶次项（或说偶次项系数均为零)。又由三角函数的有界性可知，必然要用“交错”的形式才能保证函数值不发散。再从通项公式中看出而每一项系数的分子为一，分母为该项指数的阶乘，建立在如此理解的基础上或许有助于读者朋友对公式的记忆与进一步理解。（余弦函数为偶函数，分析与正弦函数类似，读者不妨自己完成剩余的记忆方法总结工作。）

第二章、从初等数学延申的角度审视：

我们首先考察n为正整数时的牛顿二项式定理：

现在类比我们数学分析课本上将正整数n替换为任意实数α的公式

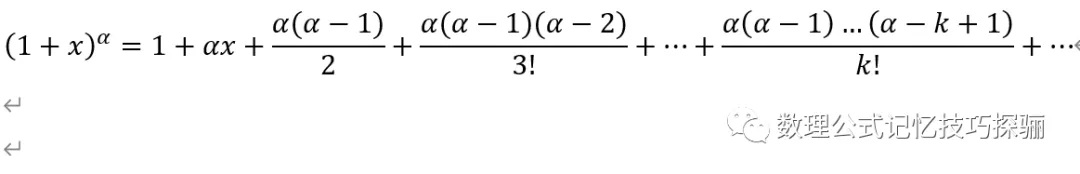
显然我们可以看出此中的高度相似性，如此我们便可轻松记忆（1+x）^α

这个函数的麦克劳林级数展开式。

第三章、从已知级数出发，并利用泰勒展开的唯一性：

在一般的数学分析课本中已经出现了很多有关泰勒展开唯一性的运用，但在笔者看来，各种现存市面上国内出版的课本均未将这种唯一性运用到淋漓尽致的程度，下面笔者将《费恩曼物理学讲义》以及《微积分学教程》中关于这方面的技巧总结出的一些体会记录如下

首先回顾我们已熟练掌握的等比级数：

下面再进行一次简单的积分操作：

综合两式，现在对等比级数展开式两边同时积分，我们不难得出

事实上，上述推导过程中已蕴含了泰勒展开的唯一性，因为我们并未用求高阶导数的方式去计算泰勒展开的系数，而是用了一定的技巧计算出级数的形式，最终我们算出结果的正确性是由泰勒展开及其唯一性来保证的。

第四章、变量替换法（尤其是复数变量替换）

回顾双曲三角函数与三角函数的定义（下图中三角函数的定义可由欧拉公式解出来，留给读者作为练习，也希望读者能长期记住该公式，十分有用）：

由此我们可以得到三角函数与双曲三角函数的关系：

现进行变量替换，令y=ix,得：

现在回顾我们在第一章节所复习的三角函数的麦克劳林展开式，并将其带入上式，最终我们得到双曲函数的麦克劳林级数表达式：

我们再次展示一遍三角函数的展开式：

比较之下我们很明显的看出三角函数的级数展开呈现“交错”的形状，而双曲函数呈现“一致”的形状，其实这不难由函数图像来直观的记忆：

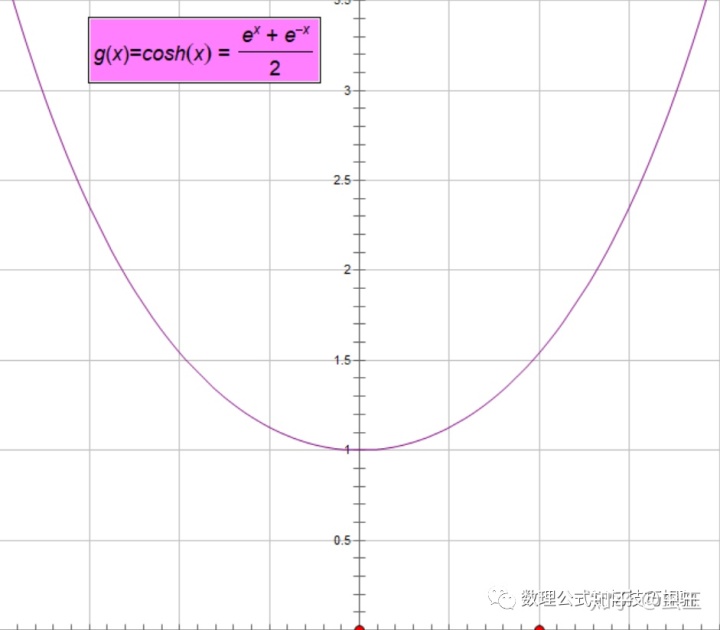
注意到三角函数的函数值是有界的，而双曲函数无此特性，因而三角函数的展开式需要用“交错”的形式来避免在x充分大时函数值发散（即维持其有界性的特点），而双曲函数展开式则要用“一致”的形式确保x充分大时，函数值也充分大。

以上是上篇的全部内容，希望读者能用心体会这些技巧，下篇将会综合以上的若干方法来解决一些新的问题。

若您觉得本文对您有帮助，欢迎关注公众号【数理tricks】获取更多记忆技巧