Brox光流法公式推导

第1章 数学基础

Brox光流法使用变分方法求解，得到使总能量最小的流场。涉及到的数学概念及工具包含：微分，变分，泛函，Euler-Lagrange equation。

1.1. 函数及微分

微分是微积分的一个基本概念，它用于描述函数在某一点附近的变化率。在物理学和工程学中，微分常被用来描述速度、加速度等与时间相关的变化率。在数学中，微分也是函数的导数，表示函数在某一点的斜率或者切线的斜率。
微分在最优化问题中有广泛应用，通过求解导数为零的点，可以找到函数的极小值或者极大值。

1.2. 泛函及变分

泛函是函数的函数。它把一个函数映射到一个实数上。泛函通常用于描述函数在一类函数中的性质，比如最小化或最大化某种性能指标。泛函最早来源于物理学，比如求解最速降曲线问题。在量子力学和统计力学中也有涉及。
求解泛函的极值可以使用变分法，比如Brox光流法中就使用了变分法。

1.3. E-L 方程

Euler-Lagrange方程是变分法中的基本方程，用于找到使泛函取得极值的函数。对于给定的泛函，Euler-Lagrange方程可以通过对泛函求导数，然后令导数为零来得到。解Euler-Lagrange方程可以得到泛函的极值函数。
有如下最小化问题：

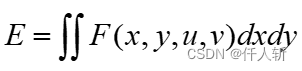
令泛函

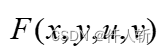
当E取极值时，根据EL方程有：

1.4. SOR

SOR,超松弛迭代法,用于迭代解决线性方程组。相比雅可比迭代和高斯-赛德尔迭代方法，收敛速度较快。
对于如下方程组：

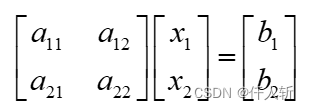
使用SOR迭代求解，迭代公式为：

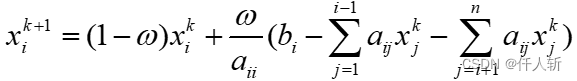
迭代求解公式为：

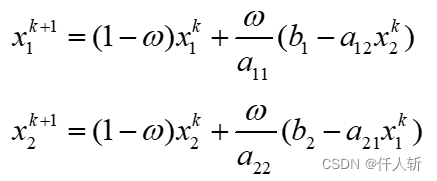
第2章 光流法基础

在运动估计，三维重建，图像配准等计算机视觉应用中，光流法是最常见的方法。
最早的光流法由Horn和Schunck在1981年提出，使用灰度约束和流场平滑约束，采用EL方程和SOR求解。以及Lucas-Kanade光流，采用灰度约束，假设光流在像素点的邻域是一个常数，使用最小二乘法求解。
为了处理流场中的不连续，PDE model将Horn和Schunck方法中的二次正则器被平滑约束取代，允许分段平滑结果。为了降低异常点干扰，Robust dynamic motion estimation方法对异常点对光流结果评价的权重降低。还有从粗到细的金字塔方案和非线性模型，用来解决大位移和局部孔径问题，比如farnback光流方法。
Brox方法综合各个方法，采用从粗到细的金字塔方案，解决大位移问题。采用非线性模型，允许流场局部有较大的变化。采用梯度约束，对图像亮暗变化有一定的适应性。

2.1. 光流法基础假设

光流法在列约束方程时，通常会对结果进行约束，常见的约束有:灰度约束，梯度约束，平滑约束。

2.1.1. 灰度约束

灰度约束是光流法中的一种常见约束条件，也称亮度约束。它假设在相邻帧之间，同一个空间点的灰度值在恒定的。这意味着，当物体在相邻帧之间移动时，它的灰度值不应该发送变化。光流法使用这个约束来建立列约束方程。
考虑一个像素 在第一帧的光强度（其中t代表其所在的时间维度）。它移动了 的距离到下一帧，用了 时间。因为是同一个像素点，根据灰度约束，可以认为该像素在运动前后的光强度是不变的，即

通常我们更喜欢线性化的模型，上式右边泰勒展开，忽略高次项，就得到了著名的光流公式：

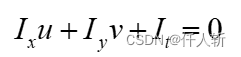
推导过程如下：
右边泰勒展开， 为二阶无穷小项

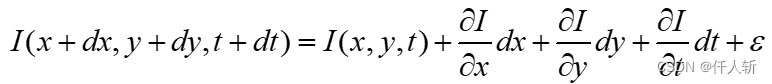
即:

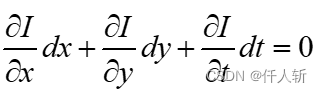
设 分别为光流分别为沿X轴与Y轴的速度矢量，得

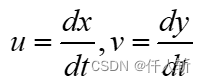
令

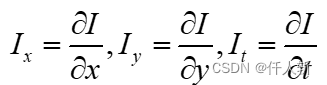
分别表示图像中像素点的灰度沿 方向的偏导数,就得到线性化后的灰度约束公式：

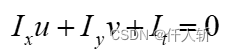
2.1.2. 梯度约束

对图像的梯度进行约束。它假设在相邻位置上，图像的梯度在方向和大小上是一致的。梯度约束可以帮助光流法更准确地估计物体的运动，尤其是在灰度有变化的有纹理、边缘明显的区域。

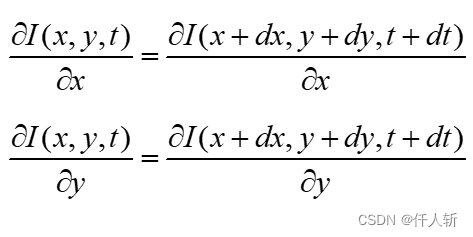
或者采用brox论文中的合并写法：

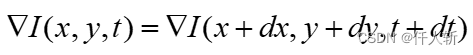
其中

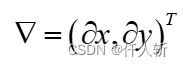
可以采用和灰度约束同样的方法进行线性化。

2.1.3. 流场平滑约束

灰度约束和梯度约束，只在局部估计了一个像素的位移，而没有考虑到相邻像素之间的任何相互作用。因此，当梯度消失，或者只能估计梯度法向方向的流动时（孔径问题），或者存在异常点时，无法准确估计光流。
流场平滑约束要求光流场在空间上是平滑的，即相邻像素点的光流向量之间的差异应该尽可能小。这个约束确保了光流场的连续性，使得估计得到的运动场更加平滑，避免了局部噪声的影响。
流场平滑约束要求流场的导 数尽可能小，即有如下的优化目标。

或者采用如下的表示方法：

此外，最优位移场在场景中物体的边界上一般是不连续的，因此通过要求分段平滑流场来推广平滑假设是合理的。
2.1.4. 流场局部常数约束
局部常数约束是平滑约束的极端情况，它要求局部的流向量是一致的，即导数为0。

Lucas-Kanade方法采用这个约束，对局部建立方程，采用最小二乘求解光流估计。

2.2. Horn-Schunck光流法

Horn-Schunck光流法使用灰度约束和流场平滑约束。采用EL方程和SOR迭代求解。
该方法使用灰度约束的线性公式，以及流场平滑约束。

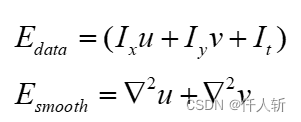
数据项和平滑项权重使用系数 调节：

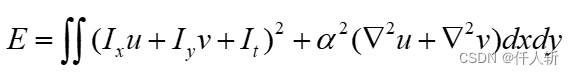
2.2.1. EL方程

令泛函

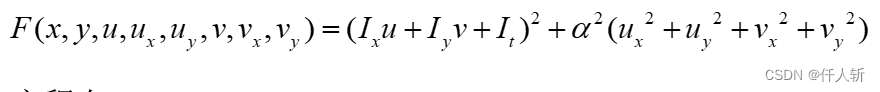
根据EL方程有：

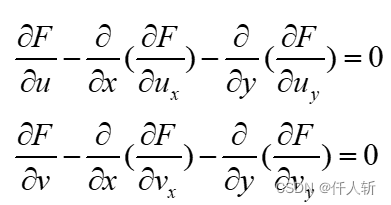
根据链式求导法则，其中：

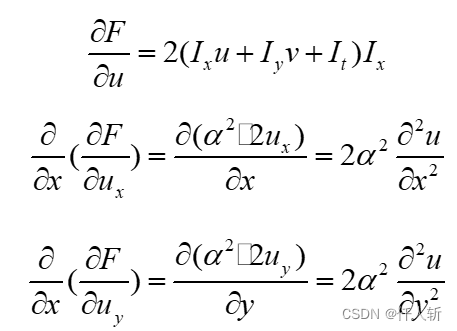
代入，得到(v的处理同理)：

因为：

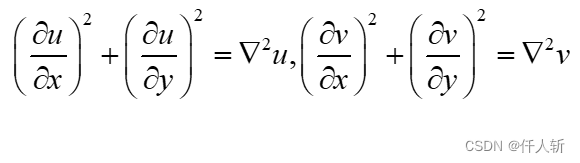
所以有：

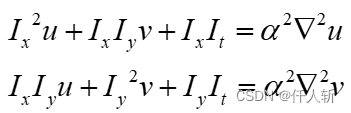
按照Horn和Schunck在1981年论文《Determining Optical Flow》中的描述，将 的计算方法,使用近似Laplace核求二阶导：

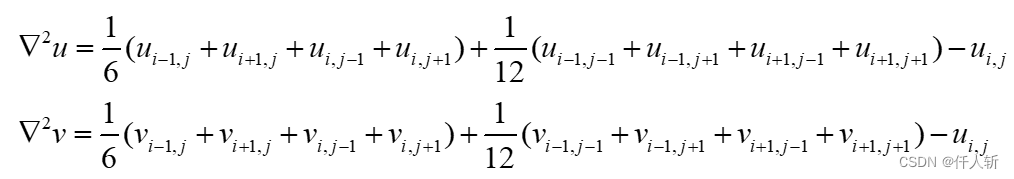
令

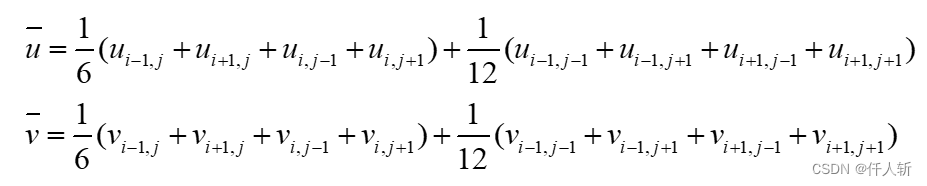
代入可得：

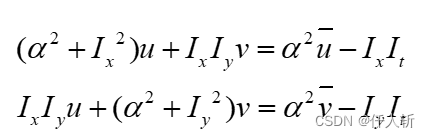
转为矩阵形式：

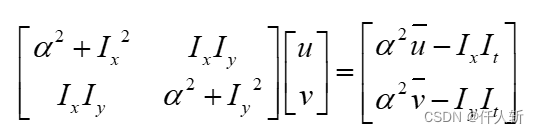
即

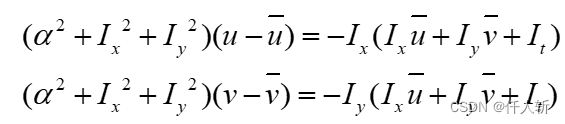
转为可以迭代的格式：

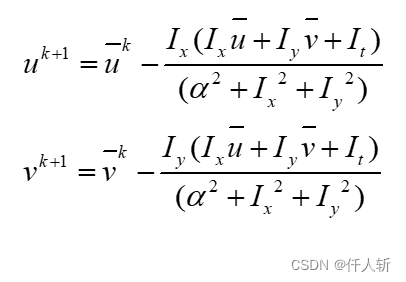
2.3. Lucas-Kanade光流法

Lucas-Kanade光流，采用灰度约束，认为光流在像素点的邻域是一个常数。假设在点 x及其邻域，光流值都为u，v ,结合灰度约束的线性假设，使用邻域4个点，则可列如下方程：

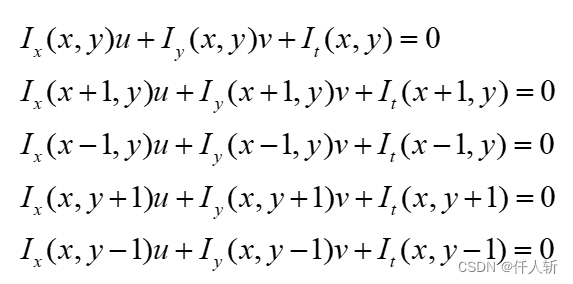
其中：

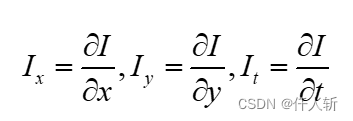
分别表示图像中像素点的灰度沿X,Y,T方向的偏导数,就得到线性化后的灰度约束公式。

2.3.1. 最小二乘法

LK光流法可以使用最小二乘法求解，步骤如下：
令：

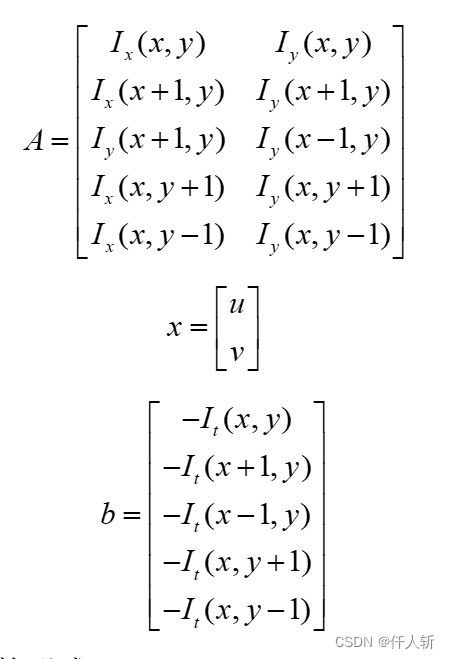
上面的等式可写成矩阵的形式：

即计算：

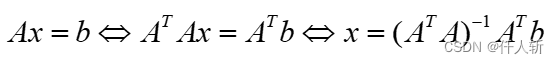
因此：

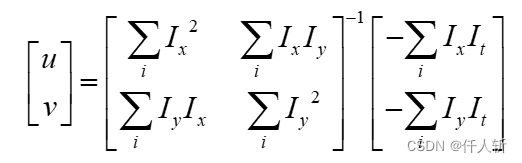
即得到了x 位置的光流值。累加参与计算的5个像素。
如果想要更多的像素参与计算，且距离中心像素越远的像素，权重越小，可加入权重矩阵，则解为：

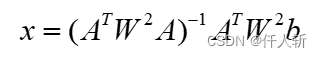
其中：

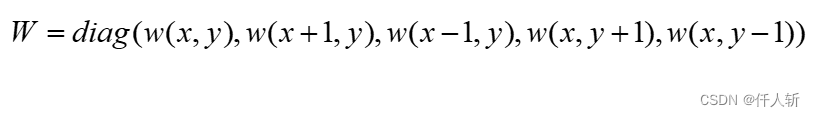
即：

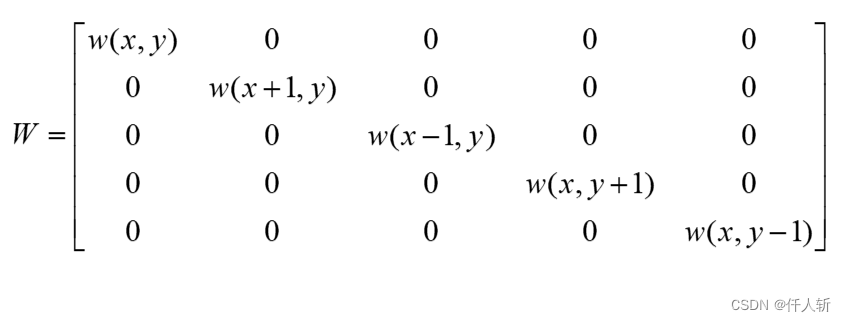
2.4. farnback光流法

Farnback光流法采用了由粗到细的策略。采用高斯金字塔方法在输入的两幅图像进行降采样。在高层金字塔的评估结果，传递到下一层级，作为初始估计。

2.4.1. 金字塔策略

Farneback采用0.5的降采样系数。而brox光流法，为了实现层间平滑的过渡，采用0.8的降采样系数。

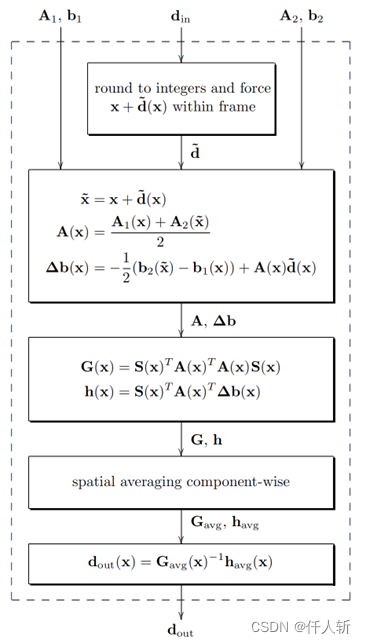
farnback每层的估计做为下一层的估计起始

2.5. 数值光流法的一般形式

以上介绍的几种典型的采用数值优化方法光流法，其优化目标一般的形式是

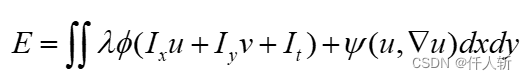
第3章 Brox光流法

Brox光流法综合了之前各种光流法的特点，采用由粗到细的，灰度约束，梯度约束和光滑约束结合的高度非线性方程，在适应大位移，孔径问题，局部流场不光滑等问题。

3.1约束方程

Brox光流法的约束项分为3个部分，分别是灰度约束，梯度约束，平滑约束。
使用向量的方式描述，令 ，

。
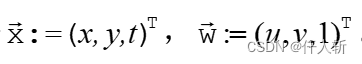
灰度约束：

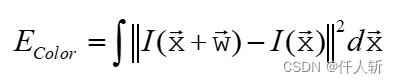
为了帮助理解，等效为：

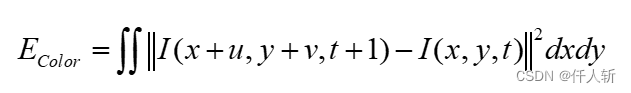
后续采用向量方式描述。
梯度约束：

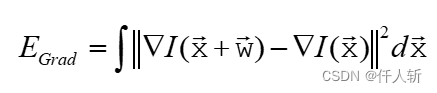
平滑约束：

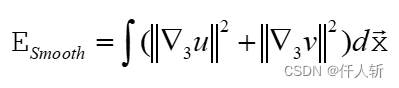
其中：

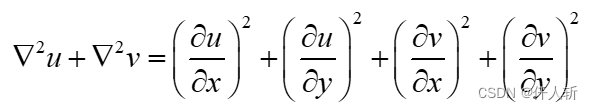
可记作

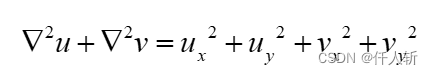
灰度约束和梯度约束中有二次项，对离群值比较敏感，因此加入一个增加凸度的函数：

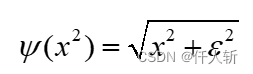
其中 取0.001。
将梯度约束和平滑约束各加入系数 和 ，得到最终约束函数：

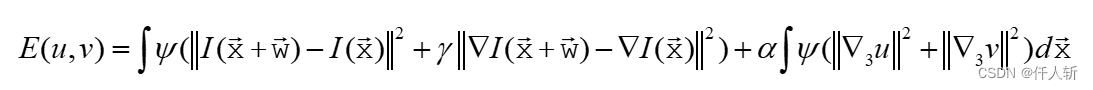
3.2 EL方程推导

令泛函：

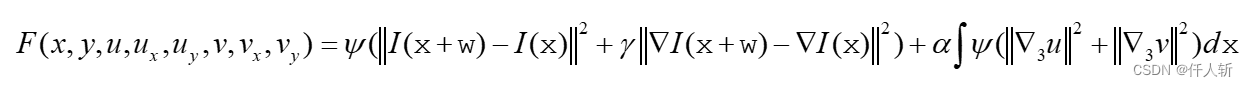
根据EL方程,当 取极值时，有：

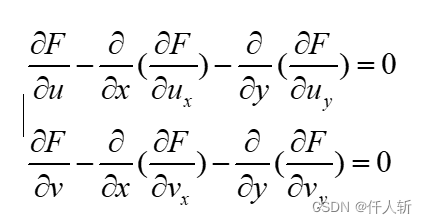
为了更好的可读性，定义如下变量：

显然有：

还是推导一下：

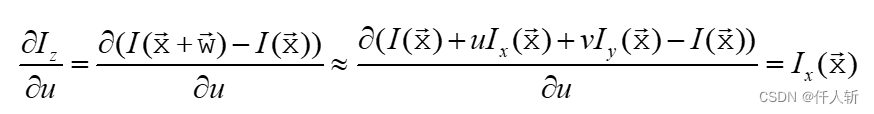
其余同理。
根据链式求导法则，其中：

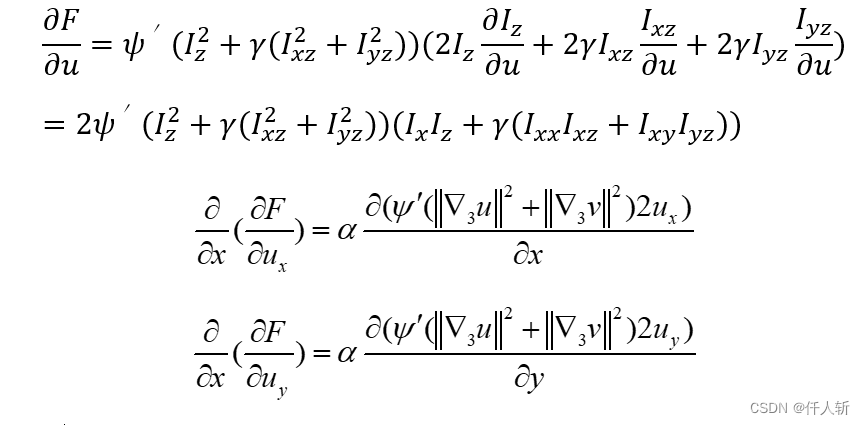
代入，可得

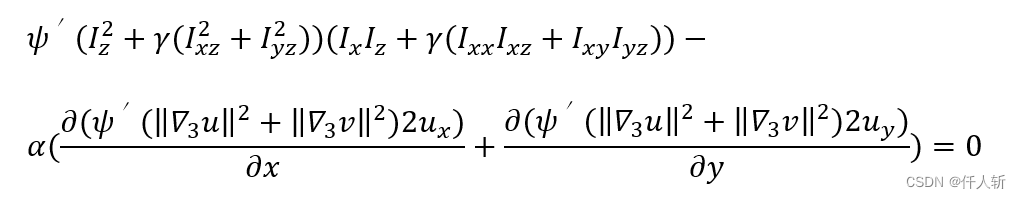
采用散度div简化为

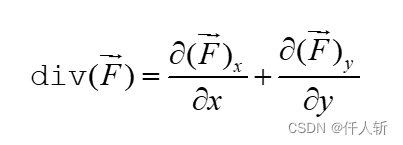
散度div表示：

同理，关于u的方程为：

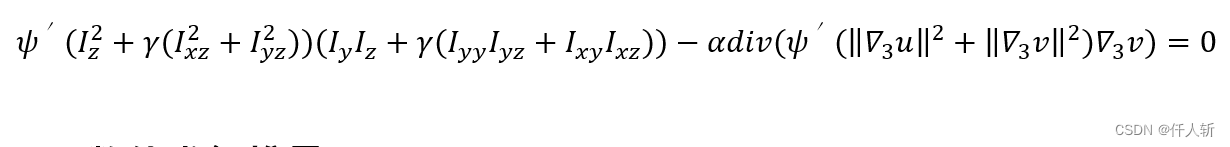
3.3 数值求解推导

前面的欧拉-拉格朗日方程在参数 中是非线性的。因此首先需要进行线性化，然后可以用常用的数值方法来求解，比如在 上使用固定点迭代。
为了实现一种多尺度的方法，更好地近似能量的全局最优，将不动点迭代与降采样策略相结合。为了实现层间更加平滑的过渡，不使用固定的0.5，而是使用 降采样系数。
采用固定点迭代的方式，外部进行k次迭代：

为了消除 中的非线性项，进行泰勒展开：

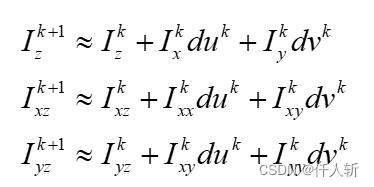
其中：

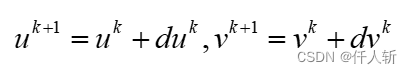
为了更好的可读性，把 中部分用如下符号代替：

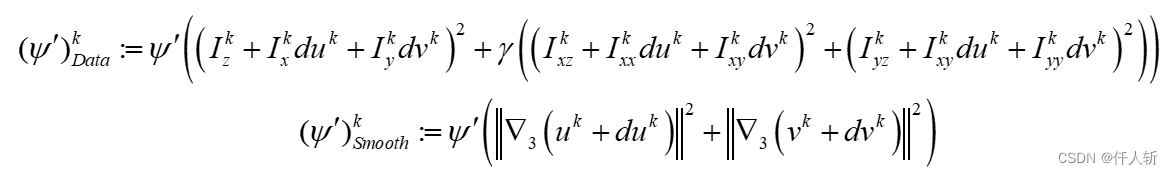
因为

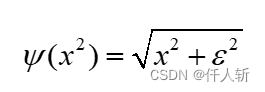
求导，有

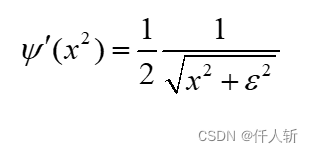
所以有

在迭代中，这部分是常数,可将 理解为鲁棒因子（robustness factor）， 理解为扩散因子（smoothness term diffusivity）。

关于v的方程同理。
由于唯一剩下的非线性是由于psai ，而 psai被选择为一个凸函数，因此剩余的优化问题是一个凸问题，即存在一个唯一的最小解。
为了去除psai 中的非线性，使用内部固定点迭代。

最终转变为关于du，dv 的线性系统：

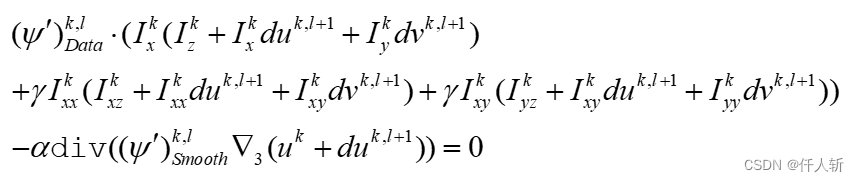
关于v的方程同理：

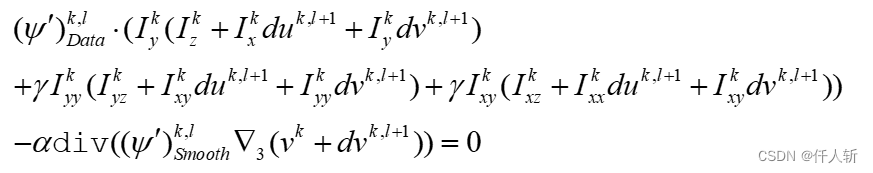
矩阵形式看的更清楚：

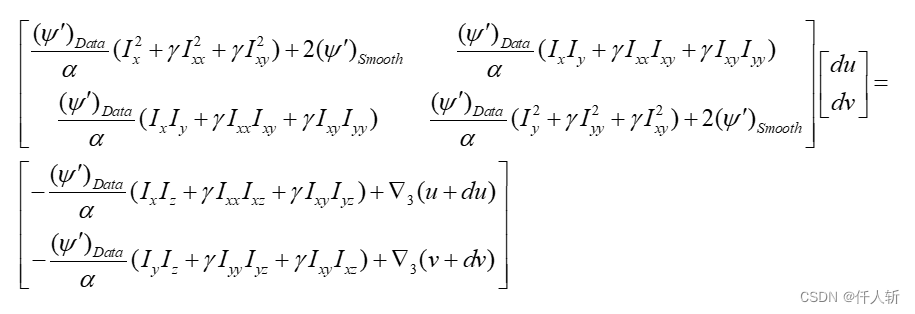
div部分拆分为：

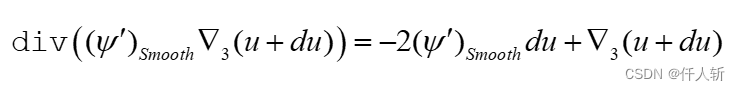
使用变量进行替换

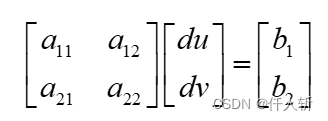
使用SOR迭代求解，迭代公式为：

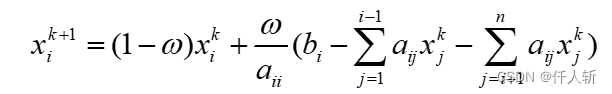
对于有2个未知数的线性方程组，有：

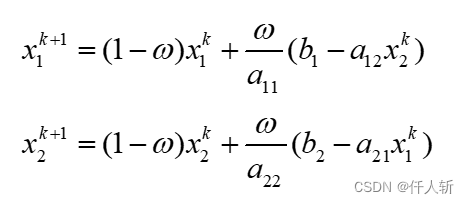
因此迭代公式为：

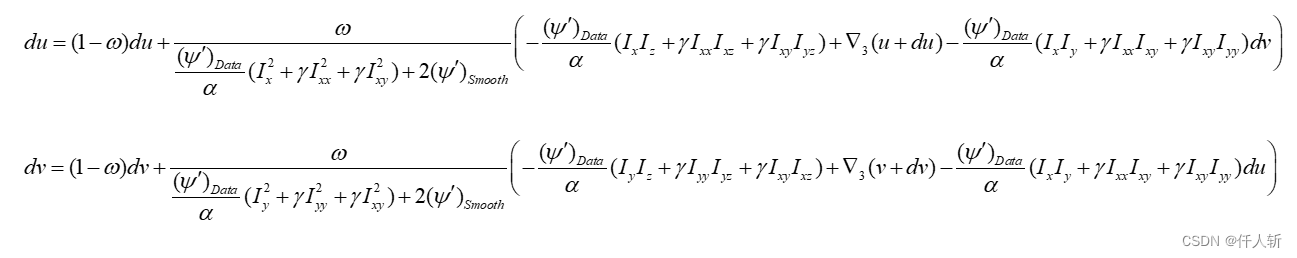
其中：

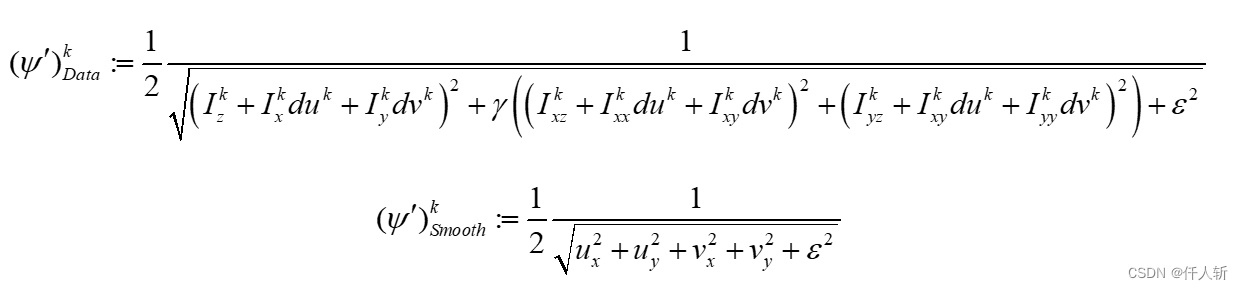
二阶导数 采用如下Laplace核：

至此，图像相关的I ,使用输入的图像的每层金字塔进行计算。每次迭代根据du，dv 计算出的u，v ，用来计算ux，uy，vx，vy 。

3.4 数值求解代码对应

3.4.1已知量

3.4.2图像相关量求解

3.4.3中间量 鲁棒因子

公式为：

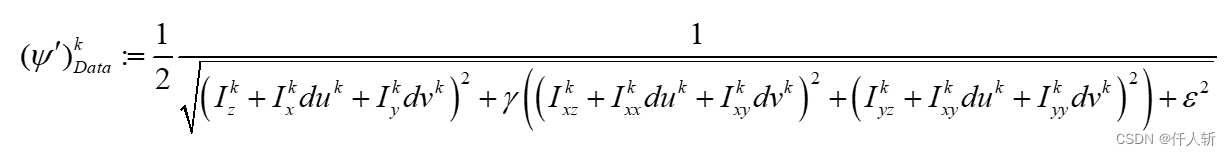
q0 = Iz + Ix * du[ijs] + Iy * dv[ijs];
q1 = Ixz + Ixx * du[ijs] + Ixy * dv[ijs];
q2 = Iyz + Ixy * du[ijs] + Iyy * dv[ijs];
data_term = 0.5f / sqrtf(q0 * q0 + gamma * (q1 * q1 + q2 * q2) + eps2);

3.4.4中间量 扩散因子

公式为：

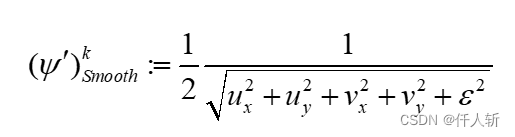
//x 导数 (i,j)  (i-1,j)  [-1 1 0]
left = pos - 1;
u_x = u[pos] + du[pos] - u[left] - du[left];
v_x = v[pos] + dv[pos] - v[left] - dv[left];
up = pos + width;
down = pos - width;
up_left = up - 1;
down_left = down - 1;
//y 导数 (i,j) (i-1,j)  [-1,0,1;-1,0,1]
u_y = 0.25f * (u[up] + du[up] + u[up_left] + du[up_left] - u[down] - du[down] - u[down_left] - du[down_left]);
v_y = 0.25f * (v[up] + dv[up] + v[up_left] + dv[up_left] - v[down] - dv[down] - v[down_left] - dv[down_left]);
*s = 0.5f / sqrtf(u_x * u_x + v_x * v_x + u_y * u_y + v_y * v_y + eps2);

3.4.5不考虑平滑项的矩阵中间量

公式为：

先计算数据项：
denominator_u：
denominator_v：
numerator_dudv：
numerator_u：
numerator_v：

	numerator_dudv = data_term * (Ix * Iy + gamma * Ixy * (Ixx + Iyy));
	numerator_u = data_term * (Ix * Iz + gamma * (Ixx * Ixz + Ixy * Iyz));
	numerator_v = data_term * (Iy * Iz + gamma * (Iyy * Iyz + Ixy * Ixz));
	denominator_u = data_term * (Ix * Ix + gamma * (Ixy * Ixy + Ixx * Ixx));
	denominator_v = data_term * (Iy * Iy + gamma * (Ixy * Ixy + Iyy * Iyy));

3.4.6加入平滑项的矩阵中间量

denominator_u,v： 加入平滑项，再预先求倒数（SOR迭代时在分母上）。

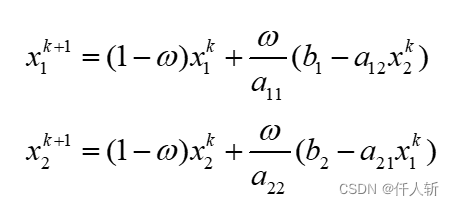
diffusivity_sum = sx[ijs] + sx[ijs + 1] + sy[ijs] + sy[ijs + PSOR_TILE_WIDTH + 1];
denom_u += diffusivity_sum;
denom_v += diffusivity_sum;
inv_denominator_u[ijg] = 1.0f / denom_u;
inv_denominator_v[ijg] = 1.0f / denom_v;

numerator_u,v： ：加入二阶导数，采用拉普拉斯核，

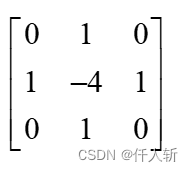
同时预先加入了SOR迭代的中间计算结果:

代码如下：

numerator_u = (s_left * (u_left + du_left) + s_up * (u_up + du_up) + s_right * (u_right + du_right) + s_down * (u_down + du_down) -
	u * (s_left + s_right + s_up + s_down) - numerator_u - numerator_dudv * dv);
numerator_v = (s_left * (v_left + dv_left) + s_up * (v_up + dv_up) + s_right * (v_right + dv_right) + s_down * (v_down + dv_down) -
	v * (s_left + s_right + s_up + s_down) - numerator_v - numerator_dudv * du);

3.4.7流向量的导数

流向量的导数ux，uy，vx，vy ，代表在x和y方向上，流图的导数。流图的导数使用的滤波核为[-1,0,1]。

3.4.8SOR迭代

SOR迭代公式为：

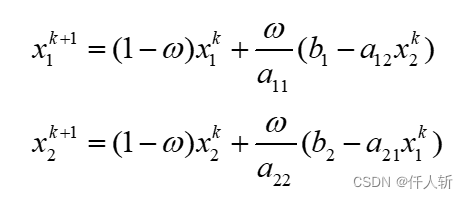
代码实现：

// 更新 du
du = (1.0f - omega) * du + omega * inv_denominator_u * numerator_u;
// 更新 dv
dv = (1.0f - omega) * dv + omega * inv_denominator_v * numerator_v;