python中的小波分解与重构 pywt.wavedec

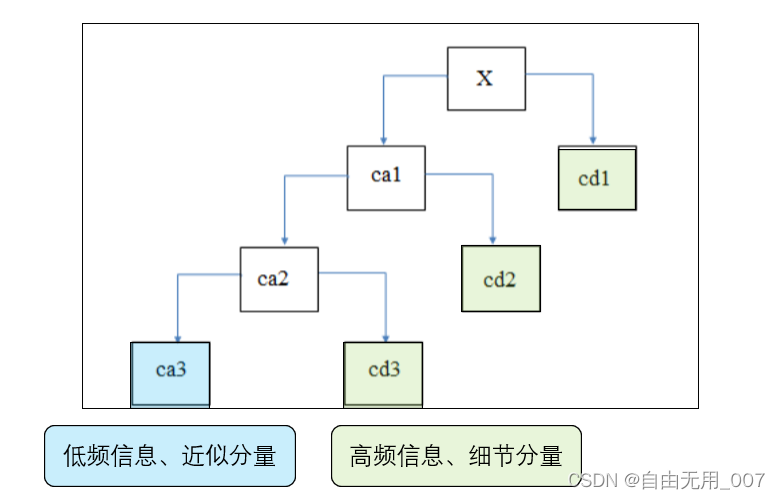
分解重构过程介绍

输入

• 数据
• 小波基
• 分解层数

输出

一个列表，包含了分解后的系数。
近似分量：结果的第一个元素是近似分量 cA_n，
细节分量 ：其余元素是细节分量 cD_n 到 cD_1。
如果是4层分解，cA_4,cD_4,cD_3,cD_2,cD_1 会得到5组系数。

coeff_all = pywt.wavedec(data, wl, level=level_n)```

这里data数据长度16384，采样频率1042，进行4层分解，采用“db1”小波基
得到的coeff_all 有五组
cA_4,系数个数1024
cD_4,系数个数1024
cD_3,系数个数2048
cD_2,系数个数4096
cD_1,系数个数8192，floor((n-1)/2)+N =floor((16384-1)/2)+2

为什么几组系数的数量不同呢？这与小波变换的原理有关：

小波系数的个数与使用的小波基有关。

DWT理论告诉我们每分解一层小波系数减半，但理论实现的算法由于加入了FB（滤波器）理论所以并不能精确的减半，其分解后小波系数的个数可以用floor((n-1)/2)+N 这个公式计算，floor表示向下取整，n是原始信号的长度，N是滤波器长度的一半。例如使用db3进行DWT，假设原始信号长度为1024，db3滤波器长度为6，则N＝3，那么系数长度为floor(511.5)+3=511+3=514。

db1滤波器长度为2，db2滤波器长度为4，db3滤波器长度为6，db4滤波器长度为8。
这里data数据长度16384，采样频率1042，进行4层分解，采用“db6”小波基
得到的coeff_all 有五组

cA_4,系数个数1034
cD_4,系数个数1034
cD_3,系数个数2057
cD_2,系数个数4104
cD_1,系数个数8197，floor((n-1)/2)+N =floor((16384-1)/2)+6

总之，小波分解的不同层次对应不同频率范围，而系数的数量随着分解层数变化。

频段划分

一个原始信号采样频率为1042hz，由采样定理得该信号的最大频率为521hz，那么对该信号做4阶的DWT，

1. 一阶细节的频段为260－521hz，逼近的频段为小于260hz
2. 二阶细节的频段为130－260hz，逼近的频段为小于130hz
3. 三阶细节的频段约为65－130hz，逼近的频段为小于65hz
4. 四阶细节的频段约为32.5－65hz，逼近的频段为小于32.5hz

分解效果如下