机器学习：支持向量机SVM原理与理解

引言

——“举牌子：Support Vector Machines ”

• 一直在犹豫要不要写SVM，因为网上已经有很多详细的SVM原理的解释甚至详细推导，而这东西又庞大复杂，想了解的话直接可以参考。说实话，SVM确实到现在也不是说很懂，感觉最恐怖的是对偶问题后的KKT推导、Mercer定理以及最后的参数求解。随便拿出来一个都是及其晦涩的数学问题。无奈水平不行，只能囫囵吞枣。
• 之所以决定要敲一下SVM的知识，大概是觉得从头到尾写一遍心里才踏实。将来回头看看，自己好像“用心”学过一遍SVM的样子。毕竟这辈子能学几个SVM呢？
• 最后一点，也是最能说服自己的一点，就是想近距离探索SVM的数学之美，向SVM的创始人及研究者致敬，向网络上的写过SVM的博主们学习。
• 下面就进入这个被冠以“迄今为止最强有监督学习分类器”、“让应用数学家真正得到应用”以及“某届G20会场外，被外国小哥高举的Support…”等称号的传奇机器学习算法——SVM。

---

初识SVM

• 关于SVM最早的一篇文章是由 Bernhard E. Boser等人在1992年发表的A training algorithm for optimal margin classifiers，感兴趣可以拜读一下这篇文章。瞻仰一下0.0（数据挖掘：理论与算法PPT中摘的图，图中引用数据截至2016）：
  
  
• 简单的概括SVM：就是寻找具有最大边缘（间隔）的超平面，位于间隔里面的平行的超平面，都能实现对数据点的线性可分。同时，面对线性不可分的情况，需要适当放宽这个间隔，引入软间隔和松弛因子。而面对更复杂的低维线性不可分的情况，通过使用核函数将数据点映射到高维，进行寻找超平面进行划分。
• 初识SVM主要介绍最大边缘超平面以及支持向量的概念。

---

1. 从线性分类器到最大边缘超平面

(1) 线性分类器

• 对于一个二维空间线性可分问题如下图所示：

• 解决上图蓝点和红圈的二分类问题，就是要找到一个超平面 $\vec w\cdot \vec x + b = 0$使得： $$\left\{ \begin{aligned} \vec w\cdot \vec x+b >0 \qquad \vec x \in \{红圈数据点\} \\ \vec w\cdot \vec x+b >0 \qquad \vec x \in \{蓝圈数据点\} \end{aligned} \right.$$ 其中，$\vec w\cdot \vec x=\sum_i w_ix_i$表示向量$\vec w={(w_1, w_2)}$ 与$\vec{x} = (x_1, x_2)$ 内积，这里的数据点用向量$\vec x$形式表示。向量$\vec w$的方向与超平面垂直。简单证明：设超平面上有两个点$\vec x_1, \vec x_2$，则$\{\vec w \cdot \vec x_1 +b = 0=\vec w \cdot \vec x_2 +b\} \Rightarrow \vec w \cdot (\vec x_1 - \vec x_2) = 0$，即向量$\vec w$与超平面垂直。
• 该超平面与分类判决准则可以构成一个线性分类器： $$f( x, w, b)=sign(g(x))=sign(w\cdot x +b)$$ 其中，$sign(\cdot)$表示符号函数。注：为了方便起见，从这里开始$w$和$x$分别表示向量$\vec w$和$\vec x$（不想每次都要敲\vec -.-，前面那样写主要是想说一下$w$的方向问题。）

(2) 点到超平面的距离

• 设二维空间存在一个超平面实现二类可分如下图所示：
  

  

• 图中的斜线表示超平面$g(x) = w \cdot x+b = 0$，二维平面上一点$X$在超平面的距离投影为$X'$，则二者关系可表示为$X=X'+\lambda w（w表示超平面的梯度向量也就是(1)中的\vec{w}）$。将$X$带入到$g(x)$得：

  $$\begin{aligned}g(X) & =w\cdot X +b \\ &=w \cdot(X'+\lambda w) + b \\& = w\cdot X' +b + \lambda w\cdot w \\ &=0+ \lambda w\cdot w = \lambda w\cdot w \end{aligned}$$

• 点到超平面的距离即是$X$与$X'$之间的距离：

  $$||X-X'||=||\lambda w|| = \frac{|g(X)|}{w\cdot w} \cdot ||w||= \frac{|g(X)|}{||w||}$$ 该公式也就是高等数学中的点到平面的距离公式，只不过这里点和平面表达式的系数都用向量表示了。这里没有从函数间隔和几何间隔的角度引入距离。同理直接带入原点坐标可得原点到超平面的距离为$\frac{|b|}{||w||}$。

(2) 最大边缘超平面

• 对于二分类问题，我们的目的就是寻找一个超平面能够实现能正确地进行划分。对于有限的训练集（数据点集）而言，存在无数个这样的超平面。
• 而有的超平面虽然能够对测试集进行很好的划分，但会出现测试数据明明很靠近一个正类却被划分到负类的情况出现。
• 因此我们要选择一个最好的超平面，在划分的时候，不偏不倚，留足两边的空余，从而达到均衡地划分。继而该超平面应用在测试集上时，能够实现稳定平衡地划分，而该平面则被称为最大边缘超平面，所谓边缘就是超平面两边的空余。如下图所示：

• 

• 下面来定量地求这个边缘宽度，假设二维空间存在二分类的数据点，设$g(x) = w\cdot x+b$，对于下图而言：

• 设正类($y_i = +1$)为红色数据点满足$g(x) = w\cdot x_i+b \ge1$，负类($y_i = -1$)为蓝色数据点满足$g(x) = w\cdot x_i+b \le-1$。设分类超平面为$g(x)= w\cdot x+b =0$，则边界上的点到该分类超平面的距离之和为$\frac{|1|}{||w||} + \frac{|-1|}{||w||}=\frac{2}{||w||}$。我们要求使得该距离之和最大的一组超平面参数。则整个过程用数学公式描述为： $$max \frac{2}{||w||} \\ s.t. \ \ y_i(w\cdot x_i +b) \ge 1$$ 问题等价于 $$min \ \frac{1}{2}||w||^2 \\ s.t. \ \ y_i(w\cdot x_i +b) \ge 1$$ 显然，这是个带有约束条件的求极值问题，问题求解在后面。

---

2. 从线性不完全可分到软间隔与松弛变量

(1) 线性不完全可分

• 线性不完全可分（这其实是自己理解的说法）：由于噪声存在或者数据本身分布有偏差（异常分布的点），现实中大多数情况下，很难实现二类问题的完美划分。如下图所示：
• 
• 图中，我们很难找到（或者说不存在）一个具有最大边缘(max margin)能够实现红蓝数据点完全分隔且最大间隔内没有数据点分布的超平面。从而造成原来的约束条件无法被满足，无法求解。

(2) 软间隔与松弛变量

• 针对线性不完全可分的问题，需要引入软间隔(soft margin)的概念：在原来的约束条件上加上一个参数适当放宽原判别准则（限制条件）： $$y_i(w\cdot x_i+b)\geq1-\xi_i$$ 其中，$\xi_i \ge 0$称为松弛变量。相应地，由于引入了松弛变量，目标函数也得到改变： $$\Phi(w) = \frac{1}{2}||w||^2+C\sum_i \xi_i$$ 其中，$C\sum_i \xi_i$为惩罚函数项，对一个异常的点的惩罚（函数）就是这个点到其正确位置（分类判决边界）的距离 （如下图所示）：
  
  
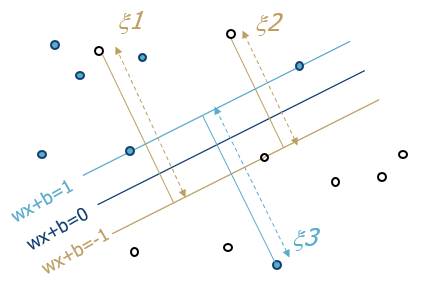
• $C$为惩罚因子表示异常分布的点对目标函数的贡献权重，C越大表示异常分布的点对目标函数$\Phi(w)$的影响就越大，使得目标函数对异常分布点的惩罚就越大。
• 因为我们需要$\frac{1}{2}||w||^2$尽可能小，同时误分类的异常点尽可能的少。C是协调两者关系的正则化惩罚系数。在实际应用中，需要调参来选择。
• 更多关于软间隔的理解与知识见参考资料。
• 至此，我们同样需要求解一个带约束条件的求极值问题： $$\begin{aligned} &min \ \ \frac{1}{2} ||w||^2 + C\sum_i \xi_i \\ &s.t.\ \ y_i(w\cdot x_i +b) \ge 1-\xi_i \\ &\qquad \xi_i \ge 0\end{aligned}$$

---

3. 从线性不可分到特征空间映射与核函数

(1) 线性不可分

• 线性不可分定义就不说了直接上图0.0：
  
  
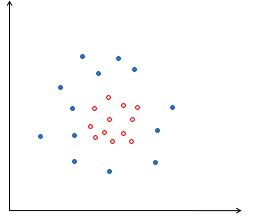
• 对于上图的二分类数据点，普通线性分类器不行，最大间隔超平面和软间隔超平面也无能为力。
• 面对这样的线性不可分问题，通常的思路是找出一个非线性分类边界（比如组合分类器）来实现分类。
• SVM则另辟蹊径，将数据点从原始空间映射到特征空间，而数据在特征空间往往就能实现线性可分。

(2) 特征空间映射

• 原始空间的线性不可分的数据点，经过映射函数$\varphi(x)$到特征空间（往往是低维到高维的映射），往往就能实现线性可分。下面用图举例说明：
• ① 一维空间向二维空间映射
  
  
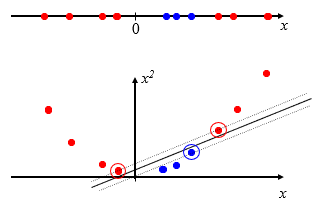
• 上图，一维空间不可分，映射到二维空间$y = x^2$就可以找到一条直线，实现二类完全可分。
• ② 二维空间向二维特征空间映射
• 
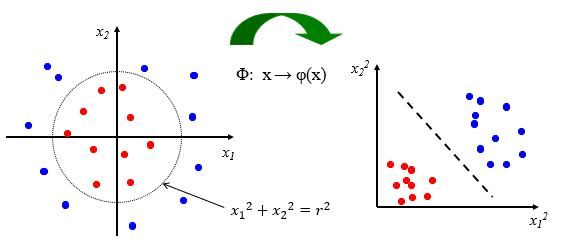
• 上图，二维空间不可分，但变换一下坐标空间，也能实现线性可分。
• ③ 二维空间向三维空间的映射
  
  
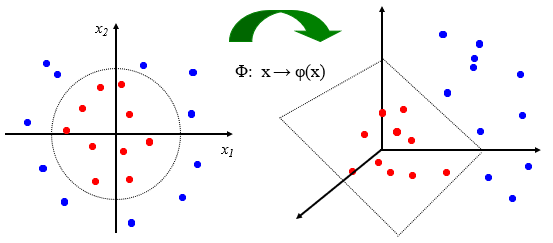
• ②中的二维空间数据点也能映射到三维空间，同样可以找到一个超平面能够实现在三维空间的线性可分。

(3) 核函数

• 原始空间向特征空间的映射需要借助映射函数$\varphi(x)$。例如对于数据点$x_i$，映射到特征空间就变成了$\varphi (x_i)$。而SVM的一大巧妙之处就是映射后的特征空间数据点内积的计算等价于低维空间数据点在映射函数对应的核函数中的计算。
• 这大大降低了运算量，因为有的时候高维空间的计算很复杂，下图是一个将$m$维向量的映射到特征空间的映射函数的例子：
• 

• 映射后的维度大概是$\frac{m^2}{2}$维。则计算映射后的数据内积$\Phi(x_i)^T \cdot \Phi(x_j)$的时间复杂度为$O(n^2)$。而如果使用核函数，则计算复杂度会降低为$O(n)$，例如：

  $$K(a, b) =(a^T \cdot b + 1)^2= \Phi(a)^T \cdot \Phi(b)$$ ，其中$a, b$为$m$维的向量，$\Phi(a)$为$a$经过上面的映射函数后的$\frac{m^2}{2}$维向量，看以看出核函数$K(a, b) =(a^T \cdot b + 1)^2$计算的时间复杂度为$O(n)$。后面会举例加以说明。

• 常用的核函数主要有：

• ① 多项式核函数： $$K(x_i, x_j)=(x_i \cdot x_j +1)^d$$ 该核函数对应的映射函数为前面的$\Phi(x)$，一个$n$维的向量映射后的特征空间向量$\Phi(x)$的维度为$C_{n+d}^d$。
• ② 高斯核函数： $$K(x_i, x_j)=exp\left(-\frac{||x_i-x_j||^2}{2\sigma^2}\right)$$ 当$x_i$和$x_j$很接近时，核函数的值约为1；相差很大时，核函数的值约为0。高斯核函数又称为径向基函数。能把原始有限维空间的向量映射到无穷维的特征空间。
• ③ S型核函数： $$K(x_i, x_j)=tanh(kx_i \cdot x_j +c)$$ 类比高斯核函数能够描述两个向量之间的相似度（0~1之间）。双曲正弦函数$tanh(\cdot)$（双极性sigmoid函数）也能作为核函数。同样地，也存在单极性sigmoid核函数。
• 还有很多其他的核函数，Mercer定理可以判断核函数的有效性。如果我们能够判断出核函数是有效的，甚至不需考虑与之对应的特征映射的函数$\Phi(x)$(实际上$\Phi(x)$很难求)，就能解决特征空间向量的内积的问题。

---

探索SVM数学之美

• 前面已经大概了解了SVM工作的基本原理，进一步了解SVM的工作原理以及求解问题，则需要深入探索SVM的数学原理。事实上，SVM中有很多晦涩难懂的数学知识，同时也有着让人拍案叫绝的数学推导。
• 下面将介绍SVM的基本数学推导及求解步骤，具体深层次的数学问题可以看附的参考资料。

---

线性可分问题的SVM求解

(1) 原始问题转化成对偶问题

• 在线性可分的SVM问题中，我们需要解决一个带有约束条件的求极值问题： $$\begin{aligned} & min\ \ \frac{1}{2}||w||^2 \\ & s.t. \ \ y_i(w\cdot x_i +b) \ge 1\end{aligned}$$
• 带有约束条件（等式约束）的求极值问题一般使用拉格朗日乘法。而上述问题的约束条件含有不等式，则需要将原问题转化为带有KKT条件的广义拉格朗日乘法的对偶问题。主要过程如下：
• 将约束条件表示为$h(x)=-y_i(w\cdot x_i +b)+1\leq 0$，原问题的拉格朗日乘法表达式为： $$\begin{aligned}L_P(w,b,\alpha) &=\frac{1}{2}||w||^2+ \alpha h(x) \\ &= \frac{1}{2}||w||^2 - \sum_i \alpha_iy_i(w\cdot x_i+b)+\sum_i \alpha_i \end{aligned}$$ 求原问题$L_P$的极小值，分别对$w$和$b$求导得： $$\begin{aligned} & \frac{\partial L_P}{\partial w}=w-\sum_i \alpha_i y_i x_i = 0 \Rightarrow w = \sum_i \alpha_i y_i x_i \\ &\frac{\partial L_P}{\partial b} =\sum_i \alpha_iy_i = 0\end{aligned}$$ 带回$L_P$得到相应得对偶问题$L_D$： $$L_D(\alpha)=\sum_i \alpha_i - \frac{1}{2}\sum_{i,j}\alpha_i \alpha_j y_i y_j (x_i)^Tx_j$$ 满足的$KKT$条件为: $$\begin{aligned} \ \ & \ \alpha_i \geq 0 \qquad (1)\\ & \sum_i \alpha_i h(x_i)= 0 \qquad (2) \\ &\ h(x_i)\leq 0 \qquad (3)\end{aligned}$$ 同时，$L_D$也受约束于 $$\sum_i \alpha_iy_i = 0$$ 此时，由原问题$L_P$关于$w$和$b$求极小值转化为对偶问题$L_D$关于$\alpha$求极大值。且$L_D$只包含变量$\alpha_i$。

(2) 引入支持向量求解$w$和$b$

• 根据对偶问题以及约束条件，求出$\alpha_i$即可得到$w$和$b$，到这里我们就需要引入支持向量了。所谓支持向量就是分布在分类判决超平面（$w\cdot x_s +b = \pm 1$）的点$x_s$（用向量表示）。可以形象地理解为支撑了两个用于分类判决的超平面。
• 支持向量能够简化$w$和$b$的计算， 从KKT条件可得，只有支持向量$x_s$对应的$\alpha_i>0$，其他数据点$x_i$对应的$\alpha_i$都为0。因此计算时只需考虑支持向量： $$w = \sum_i \alpha_i y_i x_i=\sum_{s \in S} \alpha_s y_sx_s$$ 其中，$S$为支持向量的集合。
• 对于$b$： $$\begin{aligned} & y_s(w \cdot x_s +b)=1 \\ & y_s(\sum_{k\in S}\alpha_k y_k x_k^T \cdot x_s +b)=1 \\& y_s^2(\sum_{k\in S}\alpha_k y_k x_k^T \cdot x_s +b)=y_s \\& b=y_s - \sum_{k\in S}\alpha_k y_k x_k^T \cdot x_s \\取个平均值：& b = \frac{1}{|S|} \sum_{s \in S}(y_s - \sum_{k\in S}\alpha_k y_k x_k^T \cdot x_s)\end {aligned}$$
• 下面考虑一个简单的计算例子：
  
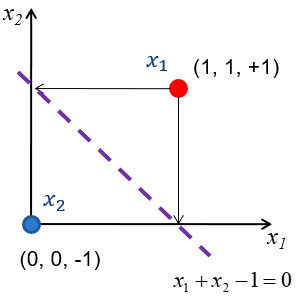
• 图中我们已知两个支持向量$x_1=(1,1), x_2=(0,0)$，对应的类别值分别为$y_1=+1, y_2=-1$。则根据原问题的约束条件得: $$\sum_{i=1}^2 \alpha_i y_i = 0 \Rightarrow \alpha_1=\alpha_2 \qquad (1)$$ 考虑对偶问题： $$L_D=\sum_{i=1}^2 \alpha_i-\frac{1}{2}\sum_{i,j=1}^2\alpha_i \alpha_j y_i y_j (x_i)^Tx_j = \alpha_1 +\alpha_2 -\alpha^2=2\alpha_1-\alpha_1^2$$ 对$L_D$求极大值，则得$\alpha_1=\alpha_2 = 1$。
• 带入求$w$和$b$： $$w=\sum_{i=1}^2 \alpha_i y_i x_i = (1,1) \\ b = -w \cdot x_1+1=-1$$
• 从而得到最大边缘超平面为： $$g(x)=w\cdot x+b = x_1 +x_2 -1=0$$
• 最大边缘间隔为：$M=\frac{2}{||w||}=\sqrt{2}$
• 这只是一个简单的示例，而且问题中只出现了支持向量对应的数据点，没有包含其他数据点。实际问题中求解很复杂，包含其他数据点具体求解$\alpha_i$需要用到SMO算法，这里不再展开。 另外关于拉格朗日对偶问题的转化更多详细信息见参考资料。

(3) 使用SVM判别未知数据点

• 还剩下一个问题，当我们计算出了$\alpha_i$，使用SVM判别一个新数据点$x^*$的分类，需要计算出$w$吗？答案是否定的，只需计算： $$\begin{aligned}y^*=w \cdot x^* +b&=\sum_{s\in S}\alpha_s y_s x_s^Tx^* +b \\&= \sum_{s\in S}\alpha_s y_s \langle x_s, x^*\rangle +b \end{aligned}$$ 其中，$\langle x_s, x^*\rangle$表示内积计算。
• 该计算说明，给定一个新的数据点$x^*$(向量表示)，我们只需计算其与支持向量的内积以及其他必要的计算。就能得出其分类判别值$y^*$，从而判断其所属类别。

---

带有软间隔的SVM求解

(1) 原始问题转化成对偶问题

• 对于线性不完全可分的软间隔SVM，同样需要求解一个带约束条件的求极值问题： $$\begin{aligned} &min \ \ \frac{1}{2} ||w||^2 + C\sum_i \xi_i \\ &s.t.\ \ y_i(w\cdot x_i +b) \ge 1-\xi_i \\ &\qquad \xi_i \ge 0\end{aligned}$$ 将约束条件表示为 $$\left\{\begin{aligned} &h(x,w,b)=-y_i(w\cdot x_i +b)+1-\xi_i \leq 0\\ & f(\xi)=-\xi_i \leq 0\end{aligned} \right.$$ 利用拉格朗日乘法得到的一个原始问题为： $$L_P(w,b,\xi,\alpha,\beta)=\frac{1}{2}||w||^2 + C\sum_i \xi_i -\sum_i \alpha_i [y_i(w\cdot x_i +b)-1+\xi_i] - \sum_i \beta_i \xi_i$$ 对$L_P$求极(小)值得： $$\begin{aligned} & \frac{\partial L_P}{\partial w}=0\Rightarrow w = \sum_i \alpha_i y_i x_i \\ &\frac{\partial L_P}{\partial b} =0 \Rightarrow\sum_i \alpha_iy_i = 0 \\ & \frac{\partial L_P}{\partial \xi_i} =0 \Rightarrow C = \alpha_i + \beta_i \end{aligned}$$ 带回$L_P$将原始问题转化为对偶问题$L_D$得： $$L_D(\alpha)=\sum_i \alpha_i - \frac{1}{2}\sum_{i,j} \alpha_i \alpha_j y_i y_j x_i^T x_j$$ 约束条件为： $$\begin{aligned} s.t. \ \ & C \ge \alpha_i \ge 0 \\ & \sum_i \alpha_i y_i = 0\end{aligned}$$ 这与不带惩罚函数以及软间隔的线性可分SVM的对偶问题及其相似，唯一的不同就是约束条件$\alpha_i$多了（$C \ge \alpha_i$）的限制。
• 由KKT条件得： $$\left\{\begin{aligned} &\alpha_i=0 \ \ \Rightarrow \ \ y_i(w\cdot x_i +b) \geq 1 \qquad（1）\\ &\alpha_i=C \ \ \Rightarrow \ \ y_i(w\cdot x_i +b) \geq 1 \qquad（2）\\ &0<\alpha_i<C \ \ \Rightarrow \ \ y_i(w\cdot x_i +b) = 1 \qquad（3）\end{aligned} \right.$$ 上式(1)表明，在两个分类判决超平面外的数据点的$\alpha_i=0$；而位于间隔内的异常点的$\alpha_i=C$；最后位于两个分类判决超平面的数据点即支持向量的$0<\alpha_i<C$。因此，在后续计算$w$和$b$的时候主要考虑支持向量以及位于软间隔内的异常数据点。

(2) SMO算法求解对偶问题

• 上面通过对原问题$L_P$的求极小值，转变成了一个求极大值的对偶问题$L_D$。即求解使得$L_D$最大的一系列$\alpha_i$的值。
• $L_D$包含一簇未知数，普通的求极值方法并不适用该问题，所以我们需要借助一些算法工具。SMO算法能够有效地求解该对偶问题。
• SMO算法Sequential Minimal Optimization A Fast Algorithm for Training Support Vector Machines由Microsoft Research的John C. Platt在1998年提出，并成为最快的二次规划优化算法，特别针对线性SVM和数据稀疏时性能更优。
• 关于SMO算法的具体工作原理这里不在展开，参考资料有两篇文章讲的很详细能够帮助更好的理解SMO算法。

---

线性不可分问题的SVM求解

(1) 特征空间的内积计算

• 前面已经提到，SVM在处理线性不可分问题时，把原始空间的数据点映射到特征空间，然后就能够通过在特征空间寻找一个超平面将特征空间里的数据点进行线性可分。
• 而从前面线性可分SVM以及带有软间隔SVM求解可知，无论是求解对偶问题，求解超平面关键参数$w$和$b$，以及对未知新数据点$x^*$的类别判别。都牵扯到一个关键的计算$x_i^T \cdot x_j$，即所谓的内积计算$\langle x_i, x_j\rangle$。
• 同样地，当数据点$x_i, x_j$通过映射函数$\varphi(\cdot)$映射到特征空间得到特征（高维）数据点$\varphi(x_i), \varphi(x_j)$时，也需要进行内积运算。实际上，将数据点映射到特征空间的求解和线性可分SVM相同。关键的一步就是特征空间的内积计算。

• 而前面同样也提到，SVM的一点巧妙之处就是能够利用核函数，把特征（一般是高维）空间的内积计算转变为在原始低维空间内数据点的计算，从而大大降低的运算复杂度。

• 下面举简例说明核函数的简化计算：

• 假设原始二维空间有两个数据点$a=(a_1, b_1)， b=(b_1, b_2)$，映射函数为$\varphi(x)=\left[ \begin{aligned} 1 \\ \sqrt{2}x_1 \\ \sqrt{2}x_2 \\ x_1^2 \\x^2\\ \sqrt{2}x_1x_2 \end{aligned} \right]$，则经过映射后，$a$和$b$在特征空间的数据点为$\varphi(a)=[1, \sqrt{2}a_1, \sqrt{2}a_2, a_1^2, a_2^2, \sqrt{2}a_1 a_2]^T, \varphi(b)=[1, \sqrt{2}b_1, \sqrt{2}b_2,$ $b_1^2,b_2^2, \sqrt{2}b_1 b_2]^T$。
• 特征空间的内积计算为： $$\begin{aligned} \varphi(a)^T \cdot \varphi(b) & = 1+ 2a_1b_1 + 2a_2b_2 + (a_1b_1)^2 + (a_2b_2)^2 + 2a_1a_2b_1b_2 \\ &= 1+ 2a_1b_1 + 2a_2b_2 + (a_1b_1 + a_2b_2)^2 \end{aligned}$$
• 从前面多项式核函数可知，该映射函数对应的核函数为$K(x_i,x_j)=(1+x_i^T\cdot x_j)^2$，则： $$\begin{aligned} K(a, b) & =(1+([a_1, b_1] \cdot \left[ \begin{aligned} b_1 \\ b_2 \end{aligned} \right]))^2 \\ &=(1+ a_1b_1 + a_2b_2)^2 \\ &=1+ 2a_1b_1 + 2a_2b_2 + (a_1b_1 + a_2b_2)^2 \end{aligned}$$ 从而得： $$\varphi(a)^T \cdot \varphi(b)=K(a, b)$$ 由此可以看出，核函数可以利用原始空间的数据样本点内积来简化特征高维空间的内积计算。

(2) 特征空间对未知数据点的分类判别

• 将数据点从原始空间映射到特征空间以后，往往就会变得线性可分。这时可以按照映射过后的特征数据点去解决对偶问题，从而求解超平面的关键参数$W$和$B$。
• 假设求得特征（高维）空间的判决超平面为$W^T \varphi(x) +B=\pm1$，则对于一个未知原始空间的数据点$x^*$该如何判别其所属类别值。需要将其带入映射函数$\varphi(\cdot)$，然后按照判决公式求解类别值吗？答案同样也是否定的。
• 事实上，有的时候$\varphi(\cdot)$无从所知或者很难知道其具体形式。所以，从$\varphi(\cdot)$出发求解则会非常麻烦。这时候，核函数就发挥关键作用了。
• 给定一个未知分类原始空间数据点$x^*$，带入特征空间的分类判别公式得： $$\begin{aligned}W^T \cdot \varphi(x^*)+B &=\left( \sum_i \alpha_i Y_i \varphi(x_i)\right)^T \cdot \varphi(x^*) +B \\ &= \sum_i \alpha_i Y_i \varphi(x_i)^T\cdot \varphi(x^*) + B \\ &= \sum_i \alpha_i Y_i K(x_i, x^*) + B\end{aligned}$$ 可以看出，类别值的最终判决结果只需在原始空间利用核函数即可计算出来，而无需考虑映射函数的参与。

---

敬畏SVM

——“人要常怀敬畏之心”

• 写到这里，关于支持向量机的大致内容算是完结了。这篇跨越五一假期的烂文总算是写完了0.0…..态度也由一开始的致敬变成了敬畏。之所以敬畏，是发现自己到现在还不算完全理解SVM，不仅仅敬畏SVM，同时敬畏经典的数学方法、敬畏复杂难懂的算法以及敬畏富有奇淫巧技的数学家。

---

难点整理

• 经过从头到尾摸索一遍SVM，大致懂了SVM的工作原理。但其中还有很多难点值得思考，由于时间和精力有限就不在深究。主要有3个难点令我印象深刻，这一点在参考资料中也有所体现：
• 一是拉格朗日乘法原始问题到对偶问题转变，以及随之产生的KKT条件。
• 二是关于软间隔的理解，惩罚函数的工作原理以及惩罚因子的确定问题。
• 三是结合KKT条件以及原始问题的约束条件的SMO算法求解问题。

总结与理解

• 这里就不总结复杂的计算原理了，也理解不了。。

• 从基本原理上进行理解和总结：

  • SVM或者从本质上说是线性SVM，其主要目的是寻找一个能够划分类别的（线性）超平面使得该超平面的两边的数据点（样本点）都属于一个类。
  • 对于在原始空间线性可分问题（包括线性完全可分和线性不完全可分），SVM通过有监督的方式利用原始数据样本点（或者说只是一些特殊的数据点：支持向量以及软间隔的异常样本点），去求解线性超平面的参数$w$（$w$其实也没必要求，只需求$\alpha_i$）和。从而最终能够跟据判决分类超平面对未知分类的样本点进行分类。
  • 而对于原始空间线性不可分问题，通常将原始数据样本点映射到特征空间（一般是高维空间）中。然后在高维空间中寻找一个线性超平面，使得该超平面能够实现类别的划分。同时，引入核函数来简化映射后的数据点在高维空间的内积计算。而对于未知分类原始样本点，也能直接带入核函数结合高维空间的判决超平面最终得知其所属类别。

• 再抛去一层基本原理来理解SVM：

  • SVM(支持向量机)之所以称为支持向量机，大概是因为支持向量起到了最为关键的作用。 试想再偌大的样本点中，我们找到了一些分布在两类边界的样本点（支持向量），是不是基本就能确定剩余的样本点类别了。
  • SVM常常会被拿来和Logistic回归分类做比较，在我看来，SVM和Logistic虽说都是寻找一个线性分类界限，但出发点不一样。SVM是以训练集两个类的边界（支持向量）来考虑划分，而Logistic是从训练集的全局来考虑划分。这也就是为什么Logistic受噪声和离群点的影响比较大。当出现一个离群点时，Logistic划定的边界很有可能会改变。而SVM这边划分的边界却可能丝毫不动（因为你离群点并不影响我支持向量）。
  • 举个很形象的例子来理解SVM：楚汉相争，以楚河汉界为界。左边是刘邦的地盘，右边是项羽的地盘。假如我们原本不知道楚河汉界，怎么划定一个界限左边是刘邦的士兵而右边是项羽的士兵。最容易的方法就是找到两边的哨兵，找到了刘邦的哨兵，则可以判断出哨兵左边驻扎的士兵都是刘邦的。同理，项羽的哨兵右边驻扎的士兵都是项羽的。通常由哨兵划分的界限应该是双方能够拉扯的最大空间。这里哨兵即是支持向量，而双方所能拉扯的最大空间楚河汉界就是最大边缘超平面。
  • 不如就畅所欲言（瞎说0.0），假如有几个误入楚地的汉兵或者潜入楚地当间谍的汉兵。他们身在楚地心在汉，而对于他们而言，仅凭楚河汉界将他们断定为楚兵或楚人未免太苛刻了。他们内心在呐喊：“我们是汉兵（汉人），只不过身在楚地”。因此应该有一个放宽的界限或者说是他们内心的“楚河汉界”，来进行划分汉兵和楚兵。而这个放宽的界限或者说内心的“楚河汉界”就是所谓的软间隔。
  • 假如在楚河汉界还没形成之前，一群壮汉在一起准备参军，不知道谁去投靠刘邦谁去投靠项羽。或者一群楚兵和汉兵乔装混在一起，分不出哪个是刘邦的人，哪个是项羽的人。随着刘邦和项羽的一声令下，双方士兵快速分离聚拢，形成两军对阵的架势。这时候从中间画一条界限，就能很明显的划分出哪边是刘邦的人哪边是项羽的人。刘邦和项羽的一声令下就是所谓的映射函数。将汉兵和楚兵拉扯到战场上这个特征空间里。

---

参考资料

清华大学，袁博副教授：【数据挖掘：理论与算法】 课程
如何通俗地讲解对偶问题？尤其是拉格朗日对偶lagrangian duality？ - 彭一洋的回答 - 知乎
拉格朗日乘子法、KKT条件、拉格朗日对偶性
SVM支持向量机三（软间隔处理规则化和不可分情况）
支持向量机原理(二) 线性支持向量机的软间隔最大化模型
支持向量机（三）核函数
支持向量机（五）SMO算法
解密SVM系列（三）：SMO算法原理与实战求解