Computational Optimal Transport 笔记——第三章(2)
常用定义
树的等价命题
3.Algorithmic Foundations
3.5 A Heuristic Description of the Network Simplex
network simplex依赖于两个简单的原则:每个可行的原始解可以对应一个互补对 ( f , g ) (f,g) (f,g)。如果这个互补对是可行的,则我们达到最优值。如果不是,可以考虑更新 P P P,使得 P P P仍然是可行的,同时它的互补对 ( f , g ) (f,g) (f,g)也被更新,它更接近可行区域。
3.5.1 Obtaining a Dual Pair Complementary to P
Simplex 首先将任意极值解
P
P
P关联一对互补对偶变量(f, g)。通过找两个向量
f
f
f和
g
g
g,对于
S
(
P
)
S(P)
S(P)中的任意
(
i
,
j
′
)
(i,j')
(i,j′),
f
i
+
g
j
=
C
i
,
j
f_i+g_j=C_{i,j}
fi+gj=Ci,j。并且保证
(
f
,
g
)
(f,g)
(f,g)是可行的。
令
s
s
s是
S
(
P
)
S(P)
S(P)的势。因为
P
P
P是极值点,因此
s
≤
n
+
m
−
1
s \leq n+m-1
s≤n+m−1。由于
G
(
P
)
G(P)
G(P)没有圈,
G
(
P
)
G(P)
G(P)是一个树或者一个森林,如图3.3所示。

对于
(
f
,
g
)
(f,g)
(f,g) 的目标是与
P
P
P互补,即应该满足在
n
+
m
n+m
n+m个变量上的
s
s
s个线性等式约束

其中
S
(
P
)
S(P)
S(P)的元素被列举为
(
i
1
,
j
1
′
)
,
.
.
.
,
(
i
s
,
j
s
′
)
(i_1, j'_1), ..., (i_s, j'_s)
(i1,j1′),...,(is,js′)。
因为
s
≤
n
+
m
−
1
<
n
+
m
s\leq n+m-1<n+m
s≤n+m−1<n+m,线性系统(3.6)总是不确定的。即在
G
(
P
)
G(P)
G(P)中对偶变量是不确定的。
考虑在
G
(
P
)
G(P)
G(P)中的一棵树。假设这个树在源点中有
k
k
k个节点
i
1
,
.
.
.
,
i
k
i_1,...,i_k
i1,...,ik,在目标节点处有
l
l
l个节点
j
1
′
,
.
.
.
,
j
l
′
j'_1,...,j'_l
j1′,...,jl′,令
r
=
d
e
f
.
k
+
l
r\xlongequal{def.} k+l
rdef.k+l,则有
r
−
1
r-1
r−1条边,对应于
f
f
f中的
k
k
k个变量、
g
g
g中的
l
l
l个变量,
r
−
1
r-1
r−1个线性等式。为了消除不确定性,我们可以在树中选择任意的根节点,并且将对应的对偶变量赋值为
0
0
0。
此时一棵树中有
r
−
1
r-1
r−1个变量&
r
−
1
r-1
r−1个约束,可以求解出树中所有的对偶变量。
从根节点开始我们可以使用广度优先或深度优先搜索遍历树,以获得一系列简单的变量赋值,这些赋值决定了树中所有其他双变量的值,例如图 3.4。这个过程对于图
P
P
P中所有的树都可重复进行,以获得与
P
P
P互补的对偶变量对
(
f
,
g
)
(f,g)
(f,g)。

3.5.2 Network Simplex Update
如果通过3.5.1的算法得到的对偶对 ( f , g ) (f,g) (f,g)是可行的,也就说对于所有的 i , j i,j i,j,我们都有 f i + g j ≤ C i , j f_i+g_j \leq C_{i,j} fi+gj≤Ci,j,根据Proposition 3.3我们得到的结果是最优的。如果存在 i , j i,j i,j有 f i + g j > C i , j f_i+g_j >C_{i,j} fi+gj>Ci,j,则网络单纯形算法发挥作用。我们首先初始化图G为 G ( P ) G(P) G(P),对应于可行解 P P P并且增加了不满足条件的边 ( i , j ′ ) (i,j') (i,j′)。会有接下来两种情况:
- G仍然是一个森林( 当增加的 ( i , j ′ ) (i,j') (i,j′)存在于两棵子树之间)。在3.5.1中提出的方法仍然可以被使用在图G上,来获得新的互补对偶向量 ( f , g ) (f,g) (f,g)。可以注意到这个增加的边(约束)移除了在 n + m n+m n+m个对偶变量之间的部分不确定性,没有对原始变量 P P P进行任何改变。这个更新被称作"degenerate"(退化),因为虽然 P i , j P_{i,j} Pi,j仍然为0,但是 ( i , j ′ ) (i,j') (i,j′)进入了图G中。 G ( P ) G(P) G(P)包含在 G G G中。
- G有一个圈。我们需要去移除
G
G
G中的边,确保
G
G
G 仍然是一个森林,同时也更新
P
P
P使得
P
P
P是可行的,并且
G
(
P
)
G(P)
G(P)包含在
G
G
G中。通过如下方法实现:增加
P
i
,
j
P_{i,j}
Pi,j(不满足条件的边
(
i
,
j
′
)
(i,j')
(i,j′)对应的权重)的值并且改进在圈中的
P
P
P中的其他元素,与Proposition 3.4中证明的过程类似的。具体的过程如下。我们记图
G
G
G中的圈为
(
i
1
,
j
1
′
)
,
(
j
1
′
,
i
2
)
,
(
i
2
,
j
2
′
)
,
.
.
.
,
(
i
l
,
j
l
′
)
,
(
j
l
′
,
i
l
+
1
)
(i_1,j'_1), (j'_1,i_2), (i_2,j'_2),...,(i_l,j'_l),(j'_l,i_{l+1})
(i1,j1′),(j1′,i2),(i2,j2′),...,(il,jl′),(jl′,il+1),其中
i
1
=
i
l
+
1
=
i
i_1=i_{l+1}=i
i1=il+1=i,
j
1
=
j
j_1=j
j1=j,来强调圈是从增加的边
(
i
,
j
)
(i,j)
(i,j) 处开始的.
接下来,增加所有正向边 { i , j } \{i,j\} {i,j},减少所有反向边 { j k ′ , i k + 1 } \{ j'_k, i_{k+1} \} {jk′,ik+1},获得一个更新的结果 P ~ \tilde{P} P~。下式中 θ = min k P i k + 1 , j k \theta=\min_k P_{i_{k+1},j_k} θ=minkPik+1,jk,令 k ∗ = arg min k P i k + 1 , j k k^{*}=\arg \min_k P_{i_{k+1},j_k} k∗=argminkPik+1,jk。相当于在图 G G G中移除边 ( i k ∗ + 1 , j k ∗ ) (i_{k^{*}+1}, j_{k^{*}}) (ik∗+1,jk∗),使用3.5.1的方法计算新的对偶变量。

3.5.3 Inprovement of the Primal solution
虽然这未必是我们最初的动机,但可以看出,以上的操作只会提高P的成本。如果加入的边没有形成一个圈,也就是第一种情况,原始的解并未改变,当形成了圈,也就是第二种情况,
P
P
P被更新为
P
~
\tilde{P}
P~,并且如下有如下公式
我们现在使用在上节迭代中形成的对偶向量
(
f
,
g
)
(f,g)
(f,g)。他们满足
f
i
k
+
g
j
k
=
C
i
k
,
j
k
f_{i_k}+g_{j_k}=C_{i_k,j_k}
fik+gjk=Cik,jk和
f
i
k
+
1
+
g
i
k
=
C
i
k
+
1
,
j
k
f_{i_{k+1}}+g_{i_k}=C_{i_{k+1},j_{k}}
fik+1+gik=Cik+1,jk对于所有G中的初始边都成立,并且有
因为
C
i
,
j
<
f
i
+
g
j
C_{i,j}<f_i+g_j
Ci,j<fi+gj,因此这一项是负的。因此如果
θ
>
0
\theta>0
θ>0,我们有
如果
θ
=
0
\theta=0
θ=0,图
G
G
G被改变,但是
P
P
P并未改变。
n
e
t
w
o
r
k
s
i
m
p
l
e
x
a
l
g
o
r
i
t
h
m
network simplex algorithm
networksimplexalgorithm 可以被总结如下:初始化算法,使用NW corner rule 得到极值解
P
P
P,用
G
(
P
)
G(P)
G(P)初始化图
G
G
G。计算与
P
P
P互补的对偶变量
(
f
,
g
)
(f,g)
(f,g)(使用3.5.1描述的树结构求解)。接下来分两种情况讨论:
- 寻找不满足约束 C − f ⊕ g ≥ 0 C-f\oplus g \geq 0 C−f⊕g≥0的索引对。如果没有则 P P P是最优解,停止算法。如果有,进行第二步。
- 将满不足约束的一对边
(
i
,
j
′
)
(i,j')
(i,j′)加入到
G
G
G中。如果
G
G
G仍然没有圈,则按照
3.5.1
3.5.1
3.5.1更新
(
f
,
g
)
(f,g)
(f,g)。如果有圈,在圈内操作,保证
(
i
,
j
′
)
(i,j')
(i,j′)被标记为正,移除有最小流值得边,如图3.5一般更新
P
P
P和
G
G
G,建立相应的互补对
(
f
,
g
)
(f,g)
(f,g)。返回第一步。
被证明,此算法是多项式时间复杂度算法。
3.6 Dual Ascent Methods
不同于 network simplex,dual ascent methods 在每次迭代中保持对偶可行解,并且通过在
f
f
f和
g
g
g上加稀疏向量,使得对偶问题的目标函数值逐渐增加。
Definition 3.2 对于
S
⊂
[
n
]
S \subset [n]
S⊂[n],
S
′
⊂
[
m
]
′
=
d
e
f
.
1
′
,
.
.
.
,
m
′
S' \subset [m]'\xlongequal{def.} {1',...,m'}
S′⊂[m]′def.1′,...,m′,
1
s
∈
R
n
1_s \in R^n
1s∈Rn索引在S中的元素为1其余元素为0,对于
1
S
′
∈
R
m
1_{S'} \in R^{m}
1S′∈Rm有相同的定义。
在下文中,
(
f
,
g
)
(f,g)
(f,g)是在
R
(
C
)
R(C)
R(C)中可行对偶对,即对于所有的
(
i
,
j
′
)
∈
[
n
]
×
[
m
]
′
,
f
i
+
g
j
≤
C
i
,
j
(i,j') \in [n] \times [m]', f_i+g_j \leq C_{i,j}
(i,j′)∈[n]×[m]′,fi+gj≤Ci,j。我们称
(
i
,
j
′
)
(i,j')
(i,j′)是平衡对,如果
f
i
+
g
j
=
C
i
,
j
f_i+g_j=C_{i,j}
fi+gj=Ci,j,其他的称为不活跃的。接下来我们说明一个可行对偶对
(
f
,
g
)
(f,g)
(f,g)可以被以
S
S
S和
S
′
S'
S′的集合为索引的稀疏向量扰动,仍然是可行的。
Proposition 3.5 如果对于所有的
i
∈
S
i \in S
i∈S,
(
i
,
j
′
)
(i,j')
(i,j′)是平衡的(意味着
j
′
∈
S
′
j' \in S'
j′∈S′)
,
对
于
足
够
小
的
对于足够小的
对于足够小的\varepsilon>0$是可行的对偶变量,
都有
(
f
~
,
g
~
)
=
d
e
f
.
(
f
,
g
)
+
ε
(
1
S
,
−
1
S
′
)
(\tilde{f}, \tilde{g})\xlongequal{def.} (f,g)+\varepsilon (1_S,-1_{S'})
(f~,g~)def.(f,g)+ε(1S,−1S′).
在3.5.1中 network simplex的迭代背后的动力被获得。为了取得这个目标,
P
P
P逐步被更新以至于它的互补对偶对达到可行解。一个对称的方法,从可行对偶变量开始来获得可行初始问题的解
P
P
P,推动了dual ascent methods。接下来的proposition是dual ascent methods 的主要推动,它保证了
(
f
,
g
)
(f,g)
(f,g)的可行上升方向的存在性。
Proposition 3.6要不然
(
f
,
g
)
(f,g)
(f,g)是问题3.4的最优解

否则存在
S
⊂
[
n
]
,
S
′
⊂
[
m
]
′
S \subset [n], S' \subset [m]'
S⊂[n],S′⊂[m]′使得
(
f
~
,
g
~
)
=
d
e
f
.
(
f
,
g
)
+
ε
(
1
S
,
−
1
S
′
)
(\tilde{f}, \tilde{g})\xlongequal{def.} (f,g)+\varepsilon (1_S,-1_{S'})
(f~,g~)def.(f,g)+ε(1S,−1S′) 是可行的 (对于任意小的
ε
\varepsilon
ε)并且有更好的目标函数值。
dual ascent method 通过由集合
S
,
S
′
S,S'
S,S′产生的任意向量更新可行解
(
f
,
g
)
(f,g)
(f,g)。当集合
(
S
,
S
′
)
(S,S')
(S,S′)由Proposition 3.6的证明过程构造。步长
ε
\varepsilon
ε在Proposition 3.5被定义。我们推导了一种方法称为 primal-dual method。对于匹配问题,此方法退化为 Hungarian algorithm。
两种算法的不同点:
- Simplex-type methods总是保证目前的解是可行集合的极值点,寻找满足 R ( C ) R(C) R(C)的对偶解。然而dual ascent 没有做这个假设,迭代可以自由生成位于可行集内部的解。
- dual network simplex通过更新 ( f , g ) (f,g) (f,g)来产生一个初始问题的解 P P P满足边界约束但是在收敛时是非负的。dual ascent 建立 P P P,它是非负的,但是不需要满足约束条件。
3.7 Auction Algorithm(拍卖算法)
Complementary slackness(互补松弛性)可以注意到在optimal assignment problem,对于 optimal transport problem提出的原始对偶条件是更加容易公式化,因为任何极值解
P
P
P都是排列矩阵
P
σ
P_{\sigma}
Pσ,对于给定的
σ
\sigma
σ。给定最优的原始的
P
σ
∗
P_{\sigma^{*}}
Pσ∗和对偶解
f
∗
,
g
∗
f^{*}, g^{*}
f∗,g∗,我们有:
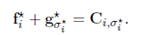
由于在3.2中阐明的 C-transforms 原则, 一个人可以选择
f
∗
=
g
C
ˉ
f^{*}=g^{\bar{C}}
f∗=gCˉ。因此,我们有
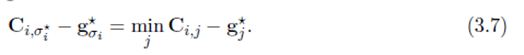
相反,如果存在满足满足如下条件的向量
g
g
g和排列
σ
\sigma
σ,则他们都是最优的,也就是说
σ
\sigma
σ是最优分配,
g
C
ˉ
g^{\bar{C}}
gCˉ和
g
g
g是最优的对偶对。
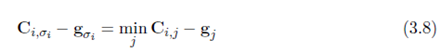
Partial assignment and
ε
−
\varepsilon-
ε− complementary slackness auction algorithm 的目标是迭代地更新三元组
S
,
ξ
,
g
S, \xi, g
S,ξ,g,其中
S
S
S是
[
n
]
[n]
[n]的子集,
ξ
\xi
ξ是一个部分分配向量,也就是从
S
S
S到
[
n
]
[n]
[n]的单射,
g
g
g是一个对偶向量。对偶向量
g
g
g收敛于满足近似互补松弛条件(3.8),
S
S
S增长逐步包含
[
n
]
[n]
[n],
ξ
\xi
ξ收敛于一个排列。在每次迭代以后算法保持一下三个性质:
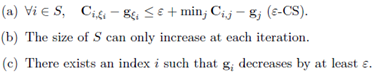
算法更新 给定一个点
j
j
j,auction algorithm 不仅使用了在一般 C-transform 中的最优值,而且使用了 second best 来定义接下来在
g
g
g上的更新,对于索引
i
∉
S
i \notin S
i∈/S,
S
S
S和
ξ
\xi
ξ。
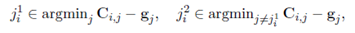
- 更新
g
g
g:将
g
g
g中
j
i
1
j_i^{1}
ji1的元素移动
ε
\varepsilon
ε、最小和第二小的调整的cost (
C
i
,
j
−
g
j
j
{C_{i,j}-g_j}_j
Ci,j−gjj)的加和
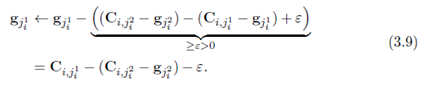
- 更新
S
S
S和
ξ
\xi
ξ:如果存在一个索引
i
′
∈
S
i' \in S
i′∈S有
ξ
i
′
=
j
i
1
\xi_{i'}=j_{i}^{1}
ξi′=ji1,移除它
设 ξ i = j i 2 \xi_{i}=j_i^2 ξi=ji2并且在 S S S中加入 i i i。(感觉原始文献中存在问题,自己修改了一下公式)

算法性质 算法从空的分配点集 S = ϕ S=\phi S=ϕ、空的部分分配向量 ξ \xi ξ,和 g = 0 n g=0_{n} g=0n开始,当 S = [ n ] S=[n] S=[n]时停止,循环执行上述两个步骤,直到终止。从公式(3.9)中可以明显地看出特性(b)和(c)成立。 ε − \varepsilon- ε−互补松弛在第一次迭代( S = ϕ S=\phi S=ϕ)是成立。通过下述的proposition可以知道特性(a)成立。
Proposition 3.7 auction algorithm在每步迭代中保存了 ε − \varepsilon- ε− 互补松弛。
Proposition 3.8 auction algorithm最多执行 N = n ∥ C ∥ ∞ / ε N=n \Vert C \Vert _{\infty}/ \varepsilon N=n∥C∥∞/ε步。
remark 3.3这个算法终止前进行了 N 3 ∥ C ∥ ∞ / ε N^3 \Vert C \Vert_{\infty}/\varepsilon N3∥C∥∞/ε此简单的操作。当使用 ε − \varepsilon- ε−scaling method时,复杂度会减少 N 3 ∥ C ∥ ∞ N^3 \Vert C \Vert_{\infty} N3∥C∥∞(在每次迭代中减少 ε \varepsilon ε的数值)。
Proposition 3.9 auction algorithm 找到了一个分配,它的费用是 n ε n\varepsilon nε次优的。
综上所述 auction algorithm可以被视为一个使用 C-transform机制的方法。接下来我们将探讨另一种基于正则化的方法,即所谓的Sinkhorn算法,它与auction算法也有相似之处。最后请注意,在欧几里得空间的低维规则网格上,可以将这些经典线性求解器与多尺度策略相结合,以获得显著的加速效果






















 1476
1476











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








