符号说明
f ⊕ g = ( f i + g j ) i , j f \oplus g=(f_i+g_j)_{i,j} f⊕g=(fi+gj)i,j
测度的累积分布函数(广义分位函数): 对于 R R R 上的测度 α \alpha α ,引入 $ R \to [0,1]$ 的 累计分布函数
2.5 对偶问题
Kantorovich问题是有约束的凸最小值问题,它可以很自然地与所谓的对偶问题配对。这个对偶问题是一个有约束的凹最大值问题。接下来的命题解释了原始问题和对偶问题的关系。
命题 2.4 Kantorovich问题有对偶
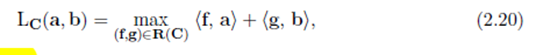
可行的对偶变量为
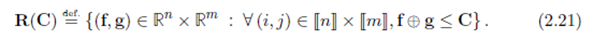
这个对偶变量被称作“Kantorovich potentials”(Kantorovich势)
证明过程:通过拉格朗日对偶问题证得。
在证明过程中可得,优化运输计划的支撑集可以缩小到
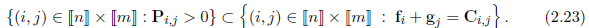
Remark 2.21 接着在 Remark 2.10 中对Kantorovich problem的解释,我们对偶进行直观的解释。一个operator希望在最小可能cost的情况下,从仓库到工厂移动全部的资源。operator可以通过求解
L
C
(
a
,
b
)
=
min
P
∈
U
(
a
,
b
)
<
C
,
P
>
=
d
e
f
.
∑
i
,
j
C
i
,
j
P
i
,
j
L_{C}(a,b)=\min_{P \in U(a,b)} <C,P> \xlongequal{def.} \sum_{i,j} C_{i,j}P_{i,j}
LC(a,b)=P∈U(a,b)min<C,P>def.i,j∑Ci,jPi,j
按照
P
∗
P^{*}
P∗中的指示,将
<
P
∗
,
C
>
<P^{*}, C>
<P∗,C>支付给运输公司。
物流外包 。 假设operator没有可计算的方法来求解上述线性规划问题。他决定将任务外包给小贩。小贩的价格规则:小贩将物流任务分解为搜集和快递物品两部分,在仓库
i
i
i搜集以单位的资源的搜集价格为
f
i
f_i
fi,无论从哪个仓库得到的物品只要是送到工厂
j
j
j的一单位资源的价格为
g
j
g_j
gj。总共,在仓库
i
i
i有
a
i
a_i
ai单位的物品,工厂
j
j
j需要
b
j
b_j
bj,小贩需要被支付的价格为
<
f
,
a
>
+
<
g
,
b
>
<f,a>+<g,b>
<f,a>+<g,b>
Setting price. 注意到被小贩使用的价格系统很自然地允许非负价格系统。如果小贩对仓库使用价格向量
f
f
f,对工厂的价格向量
g
g
g,通过以任意的数量减少
f
f
f中的所有元素并且以相同的数量增加
g
g
g中的所有元素,整体的支付价格不变(因为在仓库里的所有资源数量等于送到工厂的数量)。换句话来说小贩可以通过付钱让operator搜集商品,但是通过提高运送费补偿损失。众所周知,小贩希望收取尽可能多的费用,设置向量
f
f
f和
g
g
g尽可能的大。
Checking prices. 在缺少其余的可以竞争的小贩的情况下,operator必须检查小贩价格的合理性。可能的方法是operator计算价格
L
C
(
a
,
b
)
L_{C}(a,b)
LC(a,b)(通过求解2.11),检查小贩的价格至少不超过这个价格。但是,operator在一开始就负担不起如此冗长的计算。但是,有一种非常有效的方法来检查小贩是否提供了一个具有竞争性的策略。回忆,
f
i
f_i
fi是在
i
i
i处搜集一个单位的价格,
g
j
g_j
gj是运送到
j
j
j处的价格。因此小贩从
i
i
i运送一单位的资源到
j
j
j的价格为
f
i
+
g
j
f_i+g_j
fi+gj。同时,operator知道从通过运输公司从运送1单位的资源从
i
i
i到
j
j
j的价格
C
i
,
j
C_{i,j}
Ci,j。如果对于任何对
(
i
,
j
)
(i,j)
(i,j),
f
i
+
g
j
f_i+g_j
fi+gj严格大于
C
i
,
j
C_{i,j}
Ci,j,operator可以拒绝小贩的价格。
对偶问题的最优价格 因此operator对检查每个
(
i
,
j
)
(i,j)
(i,j)对的价格
f
i
+
g
j
≤
C
i
,
j
f_i+g_j \leq C_{i,j}
fi+gj≤Ci,j十分感兴趣。假设小贩提供的价格向量确实满足
n
×
m
n \times m
n×m个不等式,operator可以得出结论:小贩的建议是吸引人的,他接受这个offer。因为对于任何运输计划
P
P
P,都有费用
<
P
,
C
>
=
∑
i
,
j
P
i
,
j
C
i
,
j
<P,C>=\sum_{i,j} P_{i,j}C_{i,j}
<P,C>=∑i,jPi,jCi,j,operator可以通过应用这个
n
×
m
n \times m
n×m个不等式在任意的运输计划
P
P
P上(包括最优的
P
∗
P^{*}
P∗)可得出结论,边缘约束说明
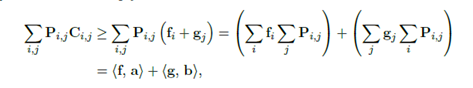
因此,请注意,任何试图自己完成工作的行为都必然比小贩的价格更昂贵。
众所周知,小贩需要找到价格集合
f
,
g
f,g
f,g最大化
<
f
,
a
>
+
<
g
,
b
>
<f,a>+<g,b>
<f,a>+<g,b>,并且有约束
f
i
+
g
j
≤
C
i
,
j
f_i+g_j \leq C_{i,j}
fi+gj≤Ci,j。得到(2.20)的等式。后面我们可以得到,小贩获得的最大价格与operator通过计算
L
C
(
a
,
b
)
L_{C}(a,b)
LC(a,b)可能花费相等。
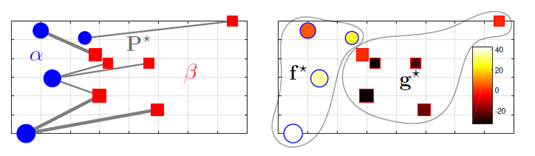
图2.8说明了来自相同的运输问题的原始和对偶解,在左边,蓝色的点代表仓库,红色的点代表工厂,点的区域代表了概率权重
a
,
b
a,b
a,b,他们之间的连线代表了最优运输,线宽与运输的数量呈比例。小贩的最优价格在右边图中体现。价格被选择,是的他们的均值为0。最高的相对价格来自于在左下方单独的仓库搜集物品和在右上方的仓库运输物品。
Remark 2.22(任意度量间的对偶问题)为了将原始-对偶结构运用到任意测度间,度量在对偶方面与连续函数搭配(测度仅可以通过连续函数的积分来访问)。对偶性在下面的命题中得到形式化表述,在处理离散测度时可归结为命题2.4。
命题 2.5有其中对偶隐变量集为
( f , g ) (f,g) (f,g)是连续变量对,在离散情况下也被称作"Kantorovich potentials"
在离散情况(2.20)对应于连续隐变量的样本组成的对偶向量, ( f i , g j ) = ( f ( x i ) , g ( y j ) ) (f_i, g_j)=(f(x_i), g(y_j)) (fi,gj)=(f(xi),g(yj))。primal-dual optiamlity条件让我们回溯到优化计划的支撑集,(2.23)可以一般化为
注意,与原始问题(2.15)相比,证明(2.24)存在非平凡的解,因为约束集合 R ( c ) \mathcal{R}(c) R(c)不是紧的,最小化函数不是强制的。使用c-transform机制(第五章)在 c ( x , y ) = d ( x , y ) p , p ≥ 1 c(x,y)=d(x,y)^p, p \geq 1 c(x,y)=d(x,y)p,p≥1 时,可证明 ( f , g ) (f,g) (f,g)是必须的 Lipschitz 正则化(使我们通过紧的代替约束)。
Remark 2.23(无约束的对偶)当 ∫ X d α = ∫ Y d β = 1 \int_{\mathcal{X}}d\alpha=\int_{\mathcal{Y}}d\beta=1 ∫Xdα=∫Ydβ=1时,约束对偶问题可以写成无约束的形式
其中 ( f ⊕ g ) ( x , y ) = f ( x ) + g ( y ) (f\oplus g)(x,y)=f(x)+g(y) (f⊕g)(x,y)=f(x)+g(y),在这里,最小值应该被认为是与度量 α ⊗ β \alpha \otimes \beta α⊗β相关的最重要的上限值,即如果在 α \alpha α和 β \beta β是0测度集上 f f f和 g g g被更新,结果并不改变。这个可替换的对偶公式是Francis
Bach提出的。可通过原始问题(2.15)加上约束 ∫ d π = 1 \int d\pi=1 ∫dπ=1得到。
Remark 2.24(Monge-Kantorovich equivalence-Brenier 定理)接下来的定理通常被认为是Brenier提出的,并且确保在 p = 2 p=2 p=2 和 R d R^{d} Rd 中,如果两个输入测度中至少有一个有密度,对于二阶矩的测度,那么Kantorovich问题和Monge问题是等价的。
定理 2.1(Brenier)在 X = Y = R d \mathcal{X}=\mathcal{Y}=R^d X=Y=Rd 和 c ( x , y ) = ∥ x − y ∥ 2 c(x,y)=\Vert x-y \Vert^2 c(x,y)=∥x−y∥2 的情况下,若两个输入测度中的一个(记为 α \alpha α)在Lebesgue测度下有密度 ρ α \rho_{\alpha} ρα,在Kantorovich公式(2.15)中的最优值 π \pi π是唯一的并且在图 ( x , T ( x ) ) (x, T(x)) (x,T(x))上,其中 “Monge map” T : R d → R d T: R^d \to R^d T:Rd→Rd。这意味着 π = ( I d , T ) # α \pi=(Id, T)_{\#}\alpha π=(Id,T)#α,即
进一步,map T T T 可以唯一被定义为一个凸函数 φ \varphi φ的梯度 T ( x ) = ∇ φ ( x ) T(x)=\nabla \varphi(x) T(x)=∇φ(x),其中 φ \varphi φ是为唯一的凸函数,有 ( ∇ φ ) # α = β (\nabla \varphi)_{\#} \alpha=\beta (∇φ)#α=β。这个凸函数与对偶隐变量 f f f相关, φ ( x ) = ∥ x ∥ 2 2 − f ( x ) \varphi(x)=\frac{\Vert x \Vert ^2}{2}-f(x) φ(x)=2∥x∥2−f(x)。
这说明在具有非奇异密度的 W 2 \mathcal{W}_2 W2的条件下,Monge problem(2.9)和 its Kantorovich relaxation(2.15)是相等的。这是 Propositon2.1的对于 assignment case(2.1)的连续性描述,这说明优化运输问题的最小化可以在排列矩阵的情况下被取得(要求边缘分布是均匀分布)。 Brenier理论说明优化运输映射一定是一个凸函数的梯度,提供维数大于1时递增函数概念的推广。这是优化运输可以被使用到定义任意维度分位函数的原因,对于分位回归问题的应用十分重要。
Remark 2.25 (Monge-Amp e ˋ \grave{e} eˋre equation)对于有密度的测度,使用(2.8)
获得 φ \varphi φ 是唯一的可以解决如下 Monge-Amp e ˋ \grave{e} eˋre equation 的凸函数
其中 ∂ 2 φ ∈ R d × d \partial^2 \varphi \in R^{d \times d} ∂2φ∈Rd×d 是 φ \varphi φ 的 Hessian。 Monge-Amp e ˋ \grave{e} eˋre operator d e t ( ∂ 2 φ ( x ) ) det(\partial^{2} \varphi(x)) det(∂2φ(x)) 可以被理解为非线性退化拉普拉斯算子。在一个小的限制 φ = I d + ε φ \varphi=Id + \varepsilon \varphi φ=Id+εφ下,可将 Laplacian Δ \Delta Δ 恢复为线性的,因为对于光滑的映射
凸的限制要求 d e t ( ∂ 2 φ ( x ) ) ≥ 0 det(\partial^{2} \varphi(x)) \geq 0 det(∂2φ(x))≥0,对于这个等式有解是必须的。
在一般情况下,主要的困难在于这个解不需要是光滑的,当输入测度是任意的时候,需要寻求 Alexandrov soluntion的机制的帮助。许多的求解方法被提出针对简单的 Monge-Amp e ˋ \grave{e} eˋre equation
f f f是固定的。
特别地,解决各向异性的凸函数要求特别的方法,一般的有限差分是不准确的。
2.6 特殊情况
Remark 2.26 (Binary cost matrix and 1-norm)当 cost matrix
C
C
C 的对角线为0,其余部分为1时,也就是说
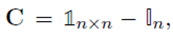
此时在
a
,
b
a, b
a,b之间的 1-Wasserstein 距离 等于他们差的 1-norm,也就是说
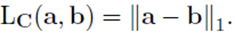
Remark 2.27(Kronecker cost function and total variantion)本部分对 Remark 2.26 扩展到任意测度的情况。对于任意测度的情况,当 c ( x , y ) = 0 c(x,y)=0 c(x,y)=0当且仅当 x = y x=y x=y, c ( x , y ) = 1 c(x,y)=1 c(x,y)=1当且仅当 x ≠ y x \neq y x=y。在两个测度 α , β \alpha, \beta α,β之间的OT距离等于他们总的距离变化量。(详见 Example 8.2)
Remark 2.28(1-D 情况——经验测度)设 X = R \mathcal{X}=R X=R。假设 α = 1 n ∑ i = 1 n δ x i \alpha= \frac{1}{n} \sum_{i=1}^{n} \delta_{x_i} α=n1∑i=1nδxi, β = 1 n ∑ i = 1 n δ y i \beta= \frac{1}{n} \sum_{i=1}^{n} \delta_{y_i} β=n1∑i=1nδyi,假设点是按照顺序排列的
因此有公式
W p ( α , β ) W_p(\alpha, \beta) Wp(α,β) 是 两个向量之间的 l p \mathcal{l}^p lp范数。
Remark 2.29(Histogram equalization)一维的 OT 可以被使用来实现 Histogram equalization(可以被应用到灰度图调色板正则化中,见 Figure 2.10)。用 ( x ˉ i ) i (\bar{x}_i)_i (xˉi)i 和 ( y ˉ j ) j (\bar{y}_j)_j (yˉj)j表示两个输入图像的所有像素的灰度水平(0-黑色,1-白色,所有的数值都在0,1之间)。假设每个图像像素点的数量是相同的,等于 n × m n \times m n×m,对这些色阶进行排序 ,定义 x i = x ˉ σ 1 ( i ) x_i=\bar{x}_{\sigma_1(i)} xi=xˉσ1(i)和 y j = y ˉ σ 2 ( j ) y_j=\bar{y}_{\sigma_2(j)} yj=yˉσ2(j),其中 σ i , σ 2 : { 1 , 2 , . . . , n m } → { 1 , 2 , . . . , n m } \sigma_i, \sigma_2:\{1,2,...,nm\} \to \{1,2,...,nm\} σi,σ2:{1,2,...,nm}→{1,2,...,nm} 是排列函数,有 σ = d e f σ 2 ∘ σ 1 − 1 \sigma \xlongequal{def} \sigma_2 \circ \sigma_1^{-1} σdefσ2∘σ1−1是两个离散分布之间的 optimal assignmet。对于图像处理的应用, ( y ˉ σ ( i ) ) i (\bar{y}_{\sigma(i)})_i (yˉσ(i))i代表了 x ˉ \bar{x} xˉ的据均衡版颜色值,他的经验分布于 y ˉ \bar{y} yˉ中的一个相匹配。通过将 n × m n \times m n×m 规模的图像拉伸成 n m nm nm维的向量,这个图像的均衡版可以被重新获得。
定义了原始图像和均衡图像之间的插值,像素点的经验分布是输入键的 displacement interpolation。
Remark 2.30 (1-D case——Generic case) 对于 R R R 上的测度 α \alpha α ,引入 $ R \to [0,1]$ 的 累计分布函数
他的伪逆
这个函数也被称为 α \alpha α的广义分位函数。 对于任何 p ≥ 1 p \geq 1 p≥1,有
这个等式说明,通过映射
Wasserstein distance 与有 L p L^p Lp norm的线性空间等距,也就是说在实线上对于测度的 Wasserstein distance 是一个 Hilbertain metric。这使得 1-D optimal transport 的几何结构非常简单,但是对于高维的空间的几何结构是非常不同的。
对于 p = 1 p=1 p=1的情况也有简单的公式
这个公式说明 W 1 W_1 W1 是一个范数。一个 optimal Monge map T (满足 T # α = β T_{\#} \alpha =\beta T#α=β)被定义为
图 2.11 说明了通过累积函数计算 1-D OT, 同样也展示了 displacement interpolations,具体计算见 (7.7), Remark 9.6。
Remark 2.31(高斯分布之间的距离) 如果 α = N ( m α , Σ α ) \alpha = \mathcal{N(m_{\alpha}, \Sigma_{\alpha})} α=N(mα,Σα), β = N ( m β , Σ β ) \beta = \mathcal{N(m_{\beta}, \Sigma_{\beta})} β=N(mβ,Σβ) 是两个在 R d R^d Rd上的高斯分布,有如下映射
有 T # ρ α = ρ β T_{\#} \rho_{\alpha}=\rho_{\beta} T#ρα=ρβ。注意到(2.8)的变形被满足,因为
因为 T T T 是线性映射,我们有
因此有
意味着
注意到 T T T 是下述凸函数的梯度
map T T T 和隐函数 ψ \psi ψ 在 Figures 2.12 和 2.13中说明。
在 ρ α \rho_{\alpha} ρα的一阶和二阶矩的计算下,我们可以获得map 的 transport cost
其中 B \mathcal{B} B 被称为在正定矩阵间的 Bures metric,
其中 Σ 1 2 \Sigma^{\frac{1}{2}} Σ21 代表矩阵的平方根。可以证明 B \mathcal{B} B 是 covariance matrices 之间的距离, B 2 \mathcal{B}^2 B2对于两个变量都是凸的。
如果 Σ α = d i a g ( r i ) i \Sigma_{\alpha}=diag(r_i)_i Σα=diag(ri)i和 Σ β = d i a g ( s i ) i \Sigma_{\beta}=diag(s_i)_i Σβ=diag(si)i是对角矩阵,Bures metirc是 Hellinger distance
对于 1-D 高斯分布,对于一维高斯分布,W2就是在二维平面上绘制高斯分布 $(m, \sqrt{\Sigma}) $的均值和标准差的欧几里德距离
Remark 2.32 (椭圆轮廓分布之间的距离)对于给定均值和方差矩阵的两个测度,满足高斯分布的测度之间的Wasserstein距离更小。如果 ρ α \rho_{\alpha} ρα和 ρ β \rho_{\beta} ρβ属于一族,即 ρ α \rho_{\alpha} ρα和 ρ β \rho_{\beta} ρβ对于每个点,使用均值和正定参数可以被写为
对于相同的非负值函数有积分
则优化运输映射是线性映射(2.40)
并且他们的 Wasserstein 距离是(2.41)







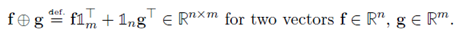
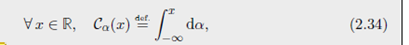
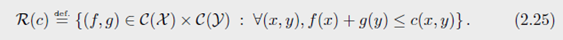
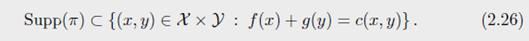
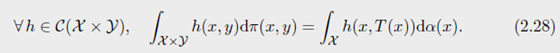
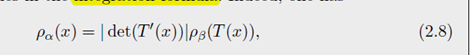
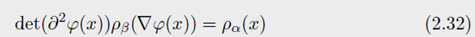
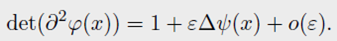
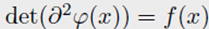
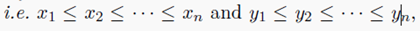
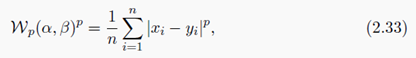

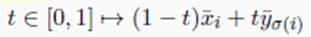

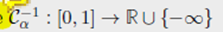
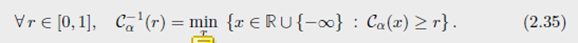
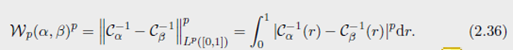
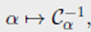
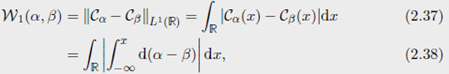



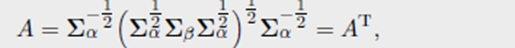
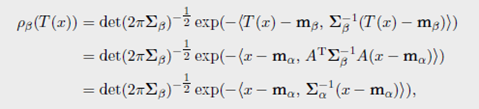
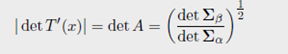

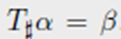
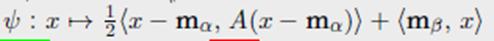

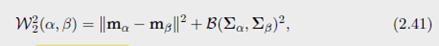
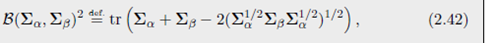
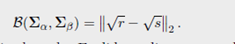

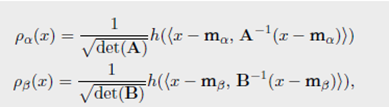
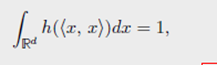
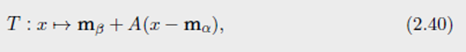
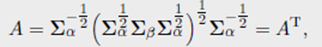
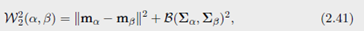














 363
363











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








