Graph Matching Networks（GMNs） 笔记

摘要

文章处理了检索和匹配图结构对象的挑战性问题。文章两个贡献：1. 证明了解决各种基于结构数据的监督预测问题高效模型graph neural networks 可以用来训练来生成向量空间中的图嵌入表示，有利于做相似推理。2. 我们提出了一个崭新的图匹配网络模型，将一对图作为输入，计算相似分数。通过一种新的基于交叉图注意力的匹配机制，对图像进行联合推理。我们证明了我们的模型在不同领域的有效性，包括基于控制流图的功能相似度搜索这一具有挑战性的问题，它在软件系统漏洞检测中起着重要的作用。

贡献

1. 我们证明了GNNs可以用来生成图嵌入，用于相似度学习
2. 我们提出了图匹配网络（graph matching matching），可以通过交叉图注意力匹配来进行计算相似度。
3. 实验表明提出的相似度学习模型可以在一系列应用上实现好的性能，比无结构模型和建立的手工设计基准上实现了更好的性能。

深度图相似学习

给定：

• $G_1=(V_1,E_1)，V_1为顶点集，E_1为边集$
• $G_2=(V_2,E_2)$

计算： 相似度得分：$s(G_1,G_2)$

• 结点特征：$x_i$
• 边特征：$e_{ij}$

3.1 图嵌入模型

模型包含3个部分：（1）编码器
（2）传播层
（3）聚合器

编码器

使用独立的MLP将点和边特征去初始化结点和边的向量表示
$$h_i^{(0)}=ML{P}_{node}(x_i),\forall i\in V$$$$e_{ij}=ML{P}_{edge}(x_{ij}),\forall (i,j)\in E$$

传播层

将顶点表示集合 { h i ( t ) } i ∈ V \{h_i^{(t)}\}_{i\in V} {hi(t)​}i∈V​映射到新的顶点表示

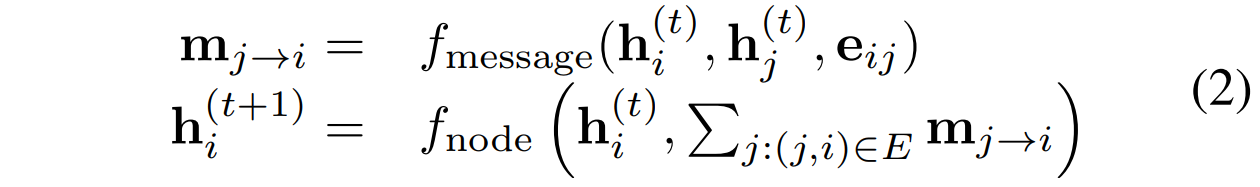
• $f_{message}$是传统串接的input上的MLP
• $f_{node}$是MLP或者是循环神经网络为核心的网络。
  领域的信息聚合可使用简单的$sum,mean,max$或者是用基于attention的权重聚合。

聚合器

经过$T$轮传播之后我们将节点表示集 { h i T } \{h_i^{T}\} {hiT​}作为输入，计算图水平的表示 h G = f G ( { h i ( T ) } ) h_G=f_G(\{h_i^{(T)}\}) hG​=fG​({hi(T)​})，我们用下面的聚合模型
这里用的是门向量去过滤掉不相关的信息。经验上来说，这比简单的相加更加有效。
将配对的$(G_1,G_2)$经过计算得到图表示$h_{G_1},h_{G_2}$，在经过向量空间中的相似度度量函数（欧式距离，cosine，海明相似度）计算相似度。

3.2 图匹配网络（GMN）

与嵌入模型相比，这些匹配模型联合计算对上的相似度评分，而不是首先独立地将每个图映射到一个向量。
提出的模型不仅仅考虑单个图中的边的信息聚合，而且考虑一个图中的一个顶点与另一个图的其他顶点的匹配度向量。即：

• $f_{message}$用来计算边信息$(i,j)\in E_1\cup E_2$
• $f_{nodee}$是MLP或者是循环神经网络为核心的网络。
• $f_{match}$表示图交叉信息，我们用attention模型计算
  - $s_h$是向量空间的相似度度量函数，像欧式或者cosine相似度。所以有

（11）式直观上来说是用来衡量$h_i^{(t)}$与另一个图上与其最近的邻接点的不同。
从(10)式可以看出规范化的系数$a_{j\to i}$依赖于 { h j ( t ) } \{h_j^{(t)}\} {hj(t)​}。

3.2 learning

1. 成对数据（$(G_1,G_2,t)$ t 为标签）

• $t\in -1,1$
• $\gamma$是边缘参数
• $d(G_1,G_2)=||h_{G_1}-h_{G_2}||$是欧式距离
• t=1表示相似，loss使得 $d<1-\gamma$
• t=-1表示不相似，$d>1+\gamma$

2. 三元输入数据$(G_1,G_2,G_3)$
   G1与G2之间的相似度小于G1与G3，所以loss 为
   这个loss 强迫$d(G_1,G_2)+\gamma <d(G_1,G_3)$
3. 图空间搜索汉明相似度改进loss
   由于图空间太大，所以如果将最后图的表示用一个二值向量会更加高效。即 h G ∈ { − 1 , 1 } H h_G\in \{-1,1\}^{H} hG​∈{−1,1}H, 所以我们最小化正例，最大化负例，也就是
   

• $s(G_1,G_2)=\frac{1}{H}{\sum }_{i=1}^{H}tanh(h_{G_{1}i})$, $tanh(h_{G_{1}i})$是近似平均汉明相似度
• 两个loss范围都是[0,1], 将正例的hamming相似度趋于1，负例的趋于-1

4. 实验

1. 图编辑距离
   图数据g1和g2之间的编辑距离定义为将g1转换为g2所需的最小编辑操作数。我们通过对具有n个节点的随机二项图$G_1$和边按概率p来抽样生成训练数据。
   
2. 基于控制流图的二进制函数相似性搜索