2017NOIP普及组真题 3. 棋盘

线上OJ：

一本通:http://ybt.ssoier.cn:8088/problem_show.php?pid=1416

核心思想:

1、由于棋盘格子为100*100, 数目不大，所以可以考虑 dfs 深搜
2、由于本题要求的是走到 最后一个格子时的最小花费。 所以在 dfs 的过程中我们可以进行 优化, 即: 走到每个格子(x,y)时 记录 走到当前格子的 最小花费 val[x][y]。这样如果在 dfs 时走到（x，y）坐标的花费已经大于历史某次走到本坐标的最低花费，则可直接跳过不处理
3、dfs 的核心判断逻辑

step1、走到（x，y）坐标的花费是否已经大于历史走到本坐标的最低花费。如果大于，则直接跳过，执行下一个dfs坐标；如果小于，则更新当前坐标的最低花费，并继续

step2、如果当前已经是最后一个格子(m, m)，则更新val[m][m] 至 ans

step3、对上下左右四个方向进行 dfs

step 3.1、检查坐标是否 越界. 如果不越界, 则继续

step 3.2、如果下一步的格子颜色为空，且上一步走到当前格子已经 使用了魔法，则跳出，进行下一轮

step 3.3、如果下一步的格子颜色为空，但上一轮 没有使用魔法，则本轮可以使用魔法，传入参数为:
$$dfs(nx,ny,cost+2,1,cl)$$
注: cost+2表示花费+2; 1 表示本轮使用了魔法; cl 表示所施魔法颜色与当前地址颜色相同

step 3.4、如果下一步地址有颜色，且与当前地址颜色相同，则传入参数为
$$dfs(nx,ny,cost,0,col[x1][y1])$$
注: 0 表示本轮未使用魔法；col[x1][y1]表示颜色

step 3.5、如果下一步地址有颜色，且与当前地址颜色不相同，则传入参数为
$$dfs(nx,ny,cost+1,0,col[x1][y1])$$
注: cost +1 表示花费+1; ，0 表示本轮未使用魔法 ；col[x1][y1]表示颜色

其中，dfs的定义为:
void dfs(int x, int y, int cost, int used, int cl)

x, y：当前棋盘格子的坐标
cost：走到当前格子的花费
used：从上一步走到当前格子是否使用魔法
cl: 从上一步走到当前格子被赋予的颜色（可能是棋盘自身的颜色，也可能是被魔法赋予的颜色）

题解代码：

解法一、深搜dfs

#include <bits/stdc++.h>
#define N 105
using namespace std;

int n, m; 
int col[N][N], val[N][N];	// col：记录每个格子的颜色    val记录走到每个格子的最低花费 
int vis[N][N]; 	// vis 记录每个格子是否被走过 
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int ans = 1e9; 

/*
x, y：当前棋盘格子的坐标    cost：走到当前格子的花费   
used：从上一步走到当前格子是否使用魔法     
cl: 从上一步走到当前格子被赋予的颜色（可能是棋盘自身的颜色，也可能是被魔法赋予的颜色） 
*/
void dfs(int x, int y, int cost, int used, int cl) 
{
    if(cost >= val[x][y])  return;	// 如果本次走到（x，y）坐标的花费已经大于历史某次走到本坐标的最低花费，则直接跳过不处理 
    else  val[x][y] = cost;	// 否则记录走到本坐标的最低花费 
    
    if (x == m && y == m)	// 如果已经到了坐标（m，m），则更新题解的最小值 
    {
        ans = min(ans, val[m][m]);
        return ;
    } 

    // 分四个方向进行dfs 
    for (int i = 0; i < 4; i ++ ) 
    {
        int x1 = x + dx[i], y1 = y + dy[i];
        
        if (x1 < 1 || x1 > m || y1 < 1 || y1 > m || (vis[x1][y1] == 1) ) continue ; // 如果越界，则进行下一轮 
	
        vis[x1][y1] = 1;
        if (col[x1][y1] == -1) // 如果下一步地址的颜色为空 
        {
            if (used)
            {
                vis[x1][y1] = 0;
                continue ;	// 且上一步走到当前格子已经使用了魔法，则跳出，进行下一轮 
            }			 
            else  // 如果上一轮没有使用魔法，则本轮可以使用魔法 
                dfs(x1, y1, cost + 2, 1, cl);	// 对下一步进行dfs，花费+2,并注明本轮已使用魔法               
        }
        else if (col[x1][y1] == cl)  // 如果下一步地址有颜色，且与当前地址颜色相同
            dfs(x1, y1, cost, 0, col[x1][y1]);	  // 则 cost 花费不变，本来未使用魔法传0  
        else                                // 如果下一步地址有颜色，且与当前地址颜色不相同 
            dfs(x1, y1, cost + 1, 0, col[x1][y1]); // 则 cost 花费+1，本轮未使用魔法传0    

        vis[x1][y1] = 0;			
    }
}

int main() 
{
    scanf("%d%d", &m, &n);
    memset(col, -1, sizeof(col));	// 初始化：棋盘颜色 
    memset(val, 0x3f, sizeof(val));	// 初始化：走到每个棋盘格子的最小花费 
    
    int x, y, c;        
    for(int i = 0; i < n; i++) 
    {
        scanf("%d%d%d", &x, &y, &c);
        col[x][y] = c;	// 存入棋盘颜色 
    }      

    vis[1][1] = 1;
    dfs(1, 1, 0, 0, col[1][1]);	// 走到坐标（1,1）的最小花费为0，没有使用魔法，(1,1)的颜色就是col[1][1] 
    
    if (ans == 1e9) printf("-1"); 
    else printf("%d\n", ans);

    return 0;
}

解法二、广搜bfs

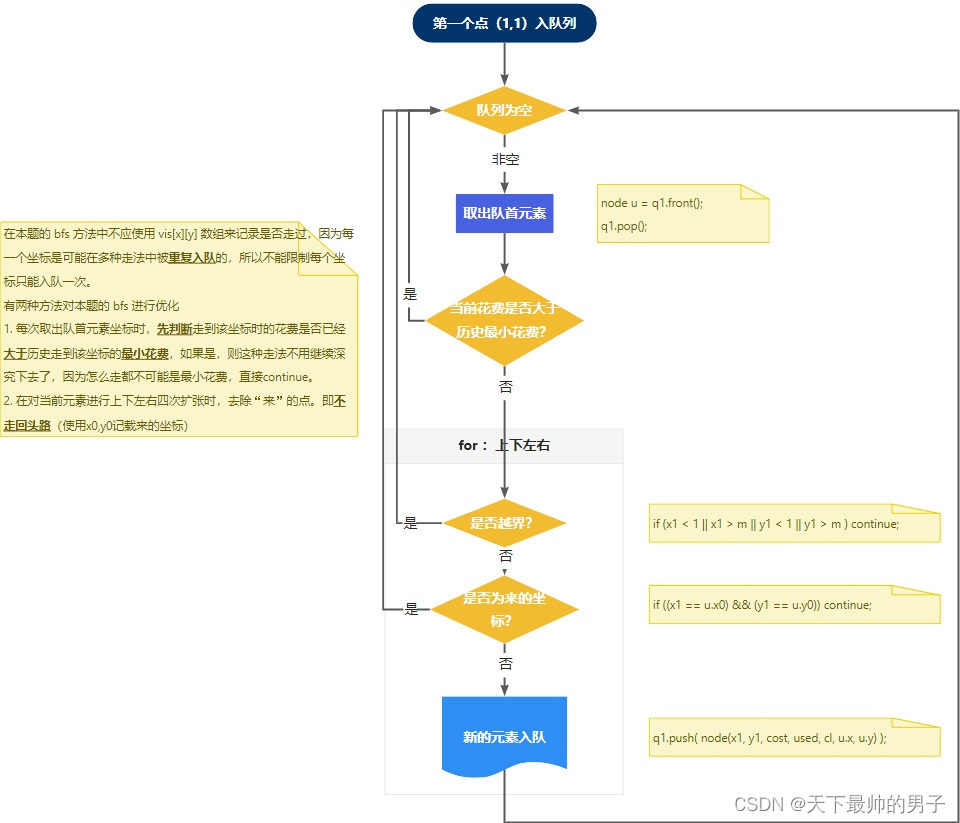
大部分情况下能用 dfs 的，也能用 bfs 来写。与上述的核心思想相同，bfs 的主流程如下

广搜bfs代码见下：

#include <bits/stdc++.h>
#define N 105
using namespace std;

int n, m; 
int col[N][N], val[N][N];	// col：记录每个格子的颜色    val记录走到每个格子的最低花费 
int vis[N][N]; 	// vis 记录每个格子是否被走过 
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int ans = 1e9; 

struct node
{
  int x, y, cost, used, cl, x0, y0;
  node(int a, int b, int z, int u, int v, int m, int n):x(a),y(b),cost(z),used(u),cl(v),x0(m),y0(n){}	//注意这对象征性地大括号不能丢。  当调用 node(a, b)时，相当于新建一个node节点，并赋值
};

/*
x, y：当前棋盘格子的坐标    cost：走到当前格子的花费   
used：从上一步走到当前格子是否使用魔法     
cl: 从上一步走到当前格子被赋予的颜色（可能是棋盘自身的颜色，也可能是被魔法赋予的颜色）
x0, y0: 记载来的坐标 
*/
void bfs(int x, int y, int cost, int used, int cl, int x0, int y0) 
{
    queue<node> q1;
    q1.push( node(x, y, cost, used, cl, x0, y0) );
  
    while( q1.empty() == false )
    {
        node u = q1.front();	// 取出队首，准备 bfs 
        q1.pop();				// 弹出	
  	
        if(u.cost >= val[u.x][u.y])  continue;	// 如果本次走到（x，y）坐标的花费已经大于历史某次走到本坐标的最低花费，则直接跳过不处理 
        else  val[u.x][u.y] = u.cost;	// 否则记录走到本坐标的最低花费 
      
        if (u.x == m && u.y == m)	// 如果已经到了坐标（m，m），则更新题解的最小值 
        {
            ans = min(ans, val[m][m]);
            continue;
        } 

        for (int i = 0; i < 4; i ++ ) 
        {
            int x1 = u.x + dx[i], y1 = u.y + dy[i];
          
            if (x1 < 1 || x1 > m || y1 < 1 || y1 > m ) continue; // 如果越界，则进行下一轮 
            if ((x1 == u.x0) && (y1 == u.y0)) continue;	// 如果是来的坐标，则跳过，不走回头路 
  		
            if (col[x1][y1] == -1) // 如果下一步地址的颜色为空 
            {
                if (u.used) continue ;	// 且上一步走到当前格子已经使用了魔法，则跳出，进行下一轮 
                else 		// 如果上一轮没有使用魔法，则本轮可以使用魔法 
                    q1.push( node(x1, y1, u.cost + 2, 1, u.cl, u.x, u.y) );
            }
            else if (col[x1][y1] == u.cl)  // 如果下一步地址有颜色，且与当前地址颜色相同
                q1.push( node(x1, y1, u.cost, 0, col[x1][y1], u.x, u.y) );
            else                                // 如果下一步地址有颜色，且与当前地址颜色不相同 
                q1.push( node(x1, y1, u.cost + 1, 0, col[x1][y1], u.x, u.y) );			
  		}	    
    }
}

int main() 
{
    scanf("%d%d", &m, &n);
    memset(col, -1, sizeof(col));	// 初始化：棋盘颜色 
    memset(val, 0x3f, sizeof(val));	// 初始化：走到每个棋盘格子的最小花费 
  
    int x, y, c;        
    for(int i = 0; i < n; i++) 
    {
        scanf("%d%d%d", &x, &y, &c);
        col[x][y] = c;	// 存入棋盘颜色 
    }      

    vis[1][1] = 1;
    bfs(1, 1, 0, 0, col[1][1], 0, 0);	// 走到坐标（1,1）的最小花费为0，没有使用魔法，(1,1)的颜色就是col[1][1] 
  
    if (ans == 1e9) printf("-1"); 
    else printf("%d\n", ans);

    return 0;
}

解法三、最短路

本题若采用最短路的核心思想：
1、将有 颜色 的 点 看成 顶点，
2、将点与点之间 可移动的路径 看成边，
3、将移动时的 花费 看成 边的权重。
则本题就变成了：求从点（1,1）到点（m,m）的最小路径。由于是单源最小路径，所以可以使用 dijkstra 算法（算法 O(N^2)，不可处理负边权。但 本题中边权为 0,1,2，所以可以使用）。

按照 dijkstra 的基本步骤（假设起点为 s， val[v]表示从s到v的最短路径（本题中为从s到v的移动最小花费））
step0、初始化val[]：val[s]=0; 其他 val[i] 都是正无穷
step1、每一轮，在 剩余的顶点 中，挑选顶点k，使val[k]是最小的；
step2、标记k点为已访问；
step3、更新与k相连的每个顶点 的最短路径；

注意：由于我们是将有 颜色 的 点 看成 顶点。题目中 只保证(1,1) 一定是有颜色的， 即 起点s 一定 存在。但 未保证目标点(m,m)是有颜色 的，故如果在有色序列中没找到(m,m)点，则需要补充这个点作为顶点，否则 dijkstra 算法跑不到这个点。

在本题中，还有一个关键点是 边权重的初始化 ：

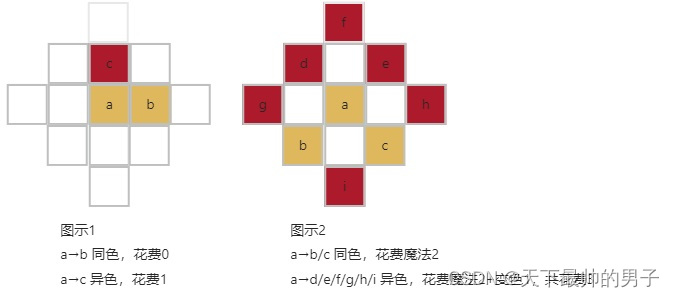
从上述图中可以发现，如果两个点之间可以移动，只有以下几种可能性

1、图示1：两个点均有颜色，且相邻。
则此时两点之间的权重 dis[i][j] 取决于颜色是否相同。如果 i 和 j 的颜色相同，则 dis[i][j] 初始化为 0，否则初始化为 1。
对应代码为：
dis[i][j] = dis[j][i] = (col[i] == col[j] ? 0 : 1);

2、图示2：两个点均有颜色，但需移动一格才能达到。
则此时两点之间的权重 dis[i][j] 依然取决于颜色是否相同。如果 i 和 j 的颜色相同，则 dis[i][j] 初始化为2（因为需要一次魔法），否则初始化为3（因为除了魔法还需要一次变色）。
对应代码为：
dis[i][j] = dis[j][i] = (col[i] == col[j] ? 2 : 3);

dijkstra 最短路代码如下：

#include <bits/stdc++.h>
#define MAXINT 0x3f3f3f3f
#define MAXN 1005 
using namespace std;

bool vis[MAXN];	// 标记每个顶点是否已被访问过 
int n, m, x[MAXN], y[MAXN], s, v, findv;		// 由于本方法使用dijkstra，故使用s记录起点；v记录终点 ;  findv表示终点v是否找到 
int dis[MAXN][MAXN], val[MAXN], col[MAXN];		// dis[i][j]表示从i移动到j的花费（0,1,2）； val[V]表示从起点s到v的最小花费（最短路径）

/*
Dijkstra 算法 O(N^2):单源最短路（不可处理负边权，本题中边权为 0,1,2）
设起点为 s， val[v]表示从s到v的最短路径（本题中为从s到v的移动最小花费）
初始化val[]：val[s]=0; 其他都是正无穷
每一轮，在剩余的顶点中，挑选顶点k，使val[k]是最小的；标记k点为已访问；更新与k相连的每个顶点的最短路径 
*/
void dijkstra()	
{
    int minval, k;
    for(int i = 1; i <= n - 1; i++) 	// 对剩余的 n-1 个顶点进行 n-1 轮 dijkstra 算法 
    {
        minval = MAXINT;
        // 在剩余的顶点中，挑选顶点k，使val[k]是最小的
        for(int j = 1; j <= n; j++)                 
            if( (vis[j] == 0) && (val[j] < minval) )
            {
                minval = val[j];
                k = j;
            }

        vis[k] = 1;  // 标记k点为已访问 
    	
        // 更新与k相连的每个顶点的最短路径 
        for(int j = 1; j <= n; j++)
            val[j] = min(val[k] + dis[k][j], val[j]);			
    }
}

int main()
{
    memset(dis, 0x3f, sizeof(dis));	// 初始化 dis 为正无穷 
    memset(val, 0x3f, sizeof(val));	// 初始化 val 为正无穷 
    memset(col, -1,   sizeof(col));	// 初始化所有颜色为 -1 
    scanf("%d%d",&m, &n);     

    for(int i = 1;i <= n; i++)
    {
        scanf("%d%d%d", &x[i], &y[i], &col[i]);

        if( x[i] == m && y[i] == m)
        {
            findv = 1;		// 找到目标点 v 
            v = i;
        }
    }
	
    if(findv == 0)	// 题中只保证(1,1)一定是有颜色的，即起点s一定存在。但未保证目标点(m,m)是有颜色的，故如果在有色序列中没找到(m,m)点，则需要补充这个点作为顶点，否则 dijkstra 找不到 
    {
        v = ++n;	// 顶点数量先+1 
        x[v] = y[v] = m;// 新增加的顶点坐标为目标点v即(m,m) 
    }
	
    // 基于有颜色的 n 个点，初始化这些点之间的边（也就是这些点之间移动的花费） ，通过画图分析可得知，只有当两个点相邻或者仅相差一步时，才能移动（也就是有边） 
    for(int i = 1; i < n; i++)
    {
        for(int j = i + 1; j <= n; j++)
        {
            if( abs(x[i] - x[j]) + abs(y[i] - y[j]) == 1)	// 如果i点和j点相邻：若i和j颜色相同，则移动时花费为0；若颜色不同，则移动时花费为1 
                dis[i][j] = dis[j][i] = (col[i] == col[j] ? 0 : 1);
            else if (abs(x[i] - x[j]) + abs(y[i] - y[j]) == 2) // 如果i点和j点相差一个空白格子：若i和j颜色相同，则移动时花费为2（仅需用魔法把空白格子变成相同颜色，此时花费为2）；若i和j颜色不同，则移动时花费为3（魔法花费2，最后异色格子之间的移动花费还有1） 
                dis[i][j] = dis[j][i] = (col[i] == col[j] ? 2 : 3);
		}
    }
	
    if(findv == 0)	// 如果目标点(m,m)是手动新增的，说明目标点为白色，需补充计算该点周围可能存在的边。此时只有一种可能，即 (m,m) 周边的点一定是有颜色的，否则无法通过两次魔法走到目标点v(m,m) 
        for(int i = 1; i <= n-1; i++)
            if( abs(x[i] - x[v]) + abs(y[i] - y[v]) == 1)
                dis[i][v] = dis[v][i] = 2;
	
    // 初始化val[]
    for(int i = 1; i <= n; i++)  val[i] = dis[1][i]; // 先用 dis[1][i] 初始化val[i]。后续在dijkstra中，val[i]会每一轮被更新一次 
    val[1] = 0;	 // 起点s到自己的花费为0 
	
    vis[1] = 1;  // 从起点1开始进行 dijkstra，故标记 vis[1]为已访问过 
    dijkstra(); 
	
    if(val[v] < 0x3f3f3f3f)	printf("%d\n", val[v]);
    else	printf("-1"); ;	
	
    return 0;
}