动态规划是什么?
动态规划(英语:Dynamic programming,简称DP)是通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。 动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法
背包九讲
1. 0-1背包
题目
有N件物品和一个容量为V的背包。第i件物品的体积是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大
这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
转移方程解析
dp[i][j]表示 只看前i个物品(i = 1...n),总体积为j情况下(j = 0...v),总价值最大是多少
result = max{ dp[n][0~v] }
dp[i][j]每次会有两个选择
1不选第i个物品,dp[i][j] = dp[i-1][j] 2选择第i个物品,dp[i][j] = dp[i-1][j - v[i]] + w[i]
所以我们得出转移方程:dp[i][j] = max{ dp[i - 1][j],dp[i - 1][j - v[i]] + w[i] }
for(int i = 1; i <= N; i++) {
for(int j = 1; j <= V; j++) {
dp[i][j] = dp[i-1][j];
if (j >= v[i]) {
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - v[i]] + w[i]);
}
}
}
System.out.println(dp[m][n]);优化二维变一维
分析下二维的过程
数据:背包总体积:7
| 价值 | 1 | 6 | 10 | 16 |
| 体积 | 1 | 2 | 3 | 5 |

发现一个特点,在决策dp[i][j]总价值最大值时,用的始终是dp[i-1],也就是二维表格中的上一行。且上一行的列不会超过当前所在列
那我们是不是可以使用一维数组,且从后往前往复遍历,避免了“i-1”行数据不被覆盖,满足上述的特点
index:0
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
构建 index :1
dp[7] = dp[7 - v[1]] + w[1] = dp[5] + 6 = 7
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 7 |
dp[6] = dp[6 - v[1]] + w[1] = dp[4] + 6 = 7
| 0 | 1 | 1 | 1 | 1 | 1 | 7 | 7 |
......
| 0 | 1 | 6 | 7 | 7 | 7 | 7 | 7 |
优化后的转移方程
dp[j] = max{ dp[j],dp[j - v[i]] + w[i] }
一维代码实现
for(int i = 1; i <= n; ++i) {
for(int j = V; j >= v[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - v[i]] + w[i]);
}
}2. 完全背包
题目
有N件物品和一个容量为V的背包,每种物品都有无限件可用。第i件物品的体积是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大
暴力解法
接着0-1背包问题,只要在放入时,增加可以添加多个物品的循环就可以了
for(int i = 1; i <= N; ++i) {
for(int j = V; j >= v[i]; j--) {
for (int k = 0; k*v[i] <= j; k++) {
dp[j] = Math.max(dp[j], dp[j - k *v[i]]+ k*w[i]);
}
}
}两层循环优化
我们思考一个问题,0-1背包时,为什么要从后往前遍历?
因为,在拆解问题时,将当前物品的是否放入建立与上一个物品最大价值之上,从后遍历是为了保留上个物品记录,且不让本次的数据“污染”上一次的记录。
但完全背包,是建立在上轮+本轮放入相同物品的基础上算总价值。试想一下,如果将遍历改为从前遍历是不是刚好符合完全背包的场景
for(int i = 1; i <= m; ++i) {
for(int j = v[i]; j <= n; j++) {
dp[j] = Math.max(dp[j], dp[j - v[i]]+ w[i]);
}
}3. 多重背包
题目
有N件物品和一个容量为V的背包,每件体积最多有si件。第i件物品的体积是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大
暴力解法
for(int i = 1; i <= m; ++i) {
for(int j = n; j >= v[i]; j--) {
for (int k = 0; k <= s&& k*v[i]<=j; k++) {
dp[j] = Math.max(dp[j], dp[j - k *v[i]]+ k*w[i]);
}
}
}二进制优化
该问题可以转化为0-1背包问题,将每种物品的si件,当做0-1背包中单独的物品,然后用0-1背包来解
但这有个问题,复杂度太高,假如有2000种物品,每种1000件,这样就会变成200w件的0-1背包问题
我们知道,数字都可以用二进制的数来表示,就是1、2、4、8.... 可以组合数任意数字,所以可以将1000件,用二进制的思想,拆成log2n件物品。最后的数字需要处理下,例如12件:可以变成1、2、4、5。 5 = 12-4-2-1
代码实现
for(int i = 1; i <= m; ++i) {
int v = in.nextInt(), w = in.nextInt(), s = in.nextInt();
for (int j = 1; j < s; j*=2) {
s-=j;
goods.add(new Good(j*v, j*w));
}
if (s > 0) {
goods.add(new Good(s*v, s*w));
}
}
for (Good good : goods) {
for (int j = n; j >= good.v; j--) {
dp[j] = Math.max(dp[j], dp[j-good.v] + good.w);
}
}4. 混合背包
题目
有N件物品和一个容量为V的背包,物品一共有三类:
●第一类物品只能用1次(01背包) ●第二类物品可以用无限次(完全背包) ●第三类物品最多只能用 si次(多重背包)
第i件物品的体积是v[i],价值是w[i]。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大
解题
这道题很简单,既然有综合了三种背包问题,我们就讲三个背包放在一起做就可以了。多重背包可以使用二进制转换为0-1背包问题,所以分两个部分:
1. 将三种物品放在一起,同时放一起将多重背包转为0-1背包
2.0-1背包/完全背包使用不同的转移方程
代码实现
for(int i = 1; i <= m; ++i) {
int v = in.nextInt(), w = in.nextInt(), s = in.nextInt();
// 0-1背包
if (s < 0) {
goods.add(new Good(-1, v, w));
}
// 完全背包
else if (s == 0) {
goods.add(new Good(0, v, w));
}
// 多重背包
else {
for (int j = 1; j <= s; j*=2) {
s-=j;
goods.add(new Good(-1,j*v, j*w));
}
if (s > 0) {
goods.add(new Good(-1,s*v, s*w));
}
}
}
for (Good good : goods) {
// 0-1背包倒序遍历
if (good.s < 0) {
for (int j = n; j >=good.v; j--) {
dp[j] = Math.max(dp[j], dp[j-good.v] + good.w);
}
}
// 完全背包正序遍历
else {
for (int j = good.v; j <= n; j++) {
dp[j] = Math.max(dp[j], dp[j-good.v] + good.w);
}
}
}5. 二维费用的背包
题目
有N件物品和一个容量为V的背包,背包能承受的最大重量是M,每件物品只能用一次,体积是vi,重量mi,价值是wi,求解将哪些物品装入背包可使这些物品的总和不超过背包容量与重量,且价值总和最大
解题
举一反三,这道题不难,回想一下我们最初的转移方程
dp[i][j][k]表示 只看前i个物品,总体积为j情况下,总价值最大是多少
那么该题的方程就是
dp[i][j][k],只看前i个物品,总体积为j,称重为k的情况下,总价值最大是多少
得出三维方程:dp[i][j][k] = max{ dp[i - 1][j][k],dp[i - 1][j - v[i]][k - m[i]] + w[i] }
优化后的方程:dp[j][k] = max{ dp[[j][k],dp[j - v[i]][k - m[i]] + w[i] }
代码
for(int i = 1; i <= N; ++i) {
int v = in.nextInt(), m = in.nextInt(), w = in.nextInt();
for(int j = V; j >= v; --j) {
for(int k = M; k >= m; --k) {
dp[j][k] = Math.max(dp[j][k], dp[j - v][k - m] + w);
}
}
}6. 分组背包
题目
有N件物品和一个容量为V的背包,每组物品有若干个,同一组内的物品最多只能选一个。每件物品的体积是 vij,价值是 wij,其中 i 是组号,j是组内编号。求解将哪些物品装入背包可使这些物品的总和不超过背包容量,且价值总和最大
解题
思考个问题:0-1背包是不是分组背包的一个特殊情况?
0-1背包实际上是分组背包,每组只有一件物品的特殊情况
所以我们再看0-1背包的转移公式
dp[i][j] = max{ dp[i - 1][j],dp[i - 1][j - v[i]] + w[i] }
结合分组背包,f[i][j]表示 只看前i个组,总体积为j情况下,总价值最大是多少,这里缺少的是每个组的选择,有 k + 1个选择情况(k为每个组物品个数)
所以dp[i][j] = max{dp[i-1][j], dp[i-1][j-v[0]] + w[0], ......,dp[i -1][j-v[k-1]]}
代码实现
// 组
for(int i = 1; i <= m; i++) {
// 每组s件物品
int s = in.nextInt();
int[] v = new int[s+1];
int[] w = new int[s+1];
for (int k = 0; k < s; k++) {
v[k] = in.nextInt();
w[k] = in.nextInt();
}
// 当前j体积
for(int j = n; j >= 0; j--) {
// 循环选择每件物品
for (int k = 0; k < s; k++) {
if (j >= v[k]) {
dp[j] = Math.max(dp[j], dp[j - v[k]] + w[k]);
}
}
}
}7. 求背包方案数
题目

这里“最优”出题者可能会分两种意思。
1.恰好装满背包,且价值最大
2.不必装满背包,且价值最大
解题
1再建一个数组,记录当前容量是j时候,方案数是多少 2看dp[j]和dp[j-v[i]]的大小,选的哪个取哪个的方案数。如果相等的话,方案数是两种方案数之和 3初始化两个数组 a将G[0] = 1 (方案数数组) 什么都不装是一种方案 其余G[1...n]为0 b如果最优为《恰好装满背包》,则将dp[0]设置为0,dp[1...n]设置为负无穷;如果为《不必装满背包》,则将dp[0...n]设置为0
为什么《恰好装满背包》就需要将dp[1...n]设置为负无穷,就可以保证“恰好装满”
解析:负无穷+常数=负无穷,所以状态方程只能从dp[0]做转移
| 0 | -INF | -INF | -INF | -INF | -INF | -INF |
假如将一个体积为3,价值为5的物品放入,得到数组,看体积4往上并没有将这个物品放入
| 0 | -INF | -INF | 5 | -INF | -INF | -INF |
再看如果初始化为0的情况得到的一维数组,但体积4往上默认把这个物品放入了
| 0 | 0 | 0 | 5 | 5 | 5 | 5 |
如果要的是恰好装满,但都初始化为0,这样算方案数的时候会把并没有装满的情况也算进来
代码
import java.util.Scanner;
public class Main {
public static void main(String[] args)
{
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int V = scan.nextInt();
int[] dp = new int[V + 1];
int[] cnt = new int[V + 1];
int v,w;
// 初始化 都为0的情况,不要求恰好装满
for(int i = 0;i <= V;i++)
{
dp[i] = 0;
}
// // 初始化为负无穷的情况,要求恰好装满
// for(int i = 1;i <= V;i++)
// {
// dp[i] = Integer.MIN_VALUE;
// }
cnt[0] = 1;
for(int i = 1;i <= n;i++)
{
v = scan.nextInt();
w = scan.nextInt();
for(int j = V,c,s;j >= v;j--)
{
c = Math.max(dp[j], dp[j - v] + w);
s = 0;
if(c == dp[j]) s += cnt[j];
if(c == dp[j - v] + w) s += cnt[j - v];
cnt[j] = s % 1000000007;
dp[j] = c;
}
}
int ans = 0,ma = 0;
for(int i = 0;i <= V;i++)
{
ma = Math.max(ma,dp[i]);
}
for(int i = 0;i <= V;i++)
{
ans += (dp[i] == ma ? cnt[i] : 0);
ans %= 1000000007;
}
System.out.print(ans);
}
}8. 求背包问题的方案
题目

解题
1字典序:两个数左对齐,从左到右每位数字依次比较,小的字典序小,如果相等继续比较下一位数字
eg: 13<14567 123235<23
2看物品是否选择,按照转移方程:dp[i][j] = max{ dp[i - 1][j],dp[i - 1][j - v[i]] + w[i] },看dp[i][j]和dp[i - 1][j],dp[i - 1][j - v[i]] + w[i]哪个相等,如果相等证明选择了当前i物品 3按字典序比较,说明如果总价值最大有1,那么最终输出必有物品1,也就是在看物品放没放要从1开始看
我们看下0-1背包完整的二维数组
数据:背包总重量:7

先看dp[3][7]=22,想知道物品3放没放,需要看dp[2][7] = 17和dp[2][2]+16 = 22。所以dp[3][7]是从dp[2][2]转移过来的,所以物品3是选择的
按照正序放物品,在分析时,是按照物品逆向顺序来分析的。所以在放物品时,需要反过来放
代码
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static int N = 1010;
static int[] v = new int[N];
static int[] w = new int[N];
static int[][] f = new int[N][N];
static int n;
static int m;
public static void main(String[] args) throws IOException{
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
String[] s1 = reader.readLine().split(" ");
n = Integer.parseInt(s1[0]);
m = Integer.parseInt(s1[1]);
for(int i = 1;i <= n;i++)
{
String[] s2 = reader.readLine().split(" ");
v[i] = Integer.parseInt(s2[0]);
w[i] = Integer.parseInt(s2[1]);
}
// 物品返着放
for(int i = n;i >= 1;i--)
{
for(int j = 0;j <= m;j++)
{
f[i][j] = f[i + 1][j];
if(j >= v[i])
{
f[i][j] = Math.max(f[i][j], f[i + 1][j - v[i]] + w[i]);
}
}
}
//f[1][m] 是最大值
int j = m;
for(int i = 1;i <= n;i ++)
{
//若当前有选该值则记录
if(j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
{
System.out.print(i + " ");
j -= v[i];
}
}
}
}9. 有依赖的背包问题(难)
题目
解题
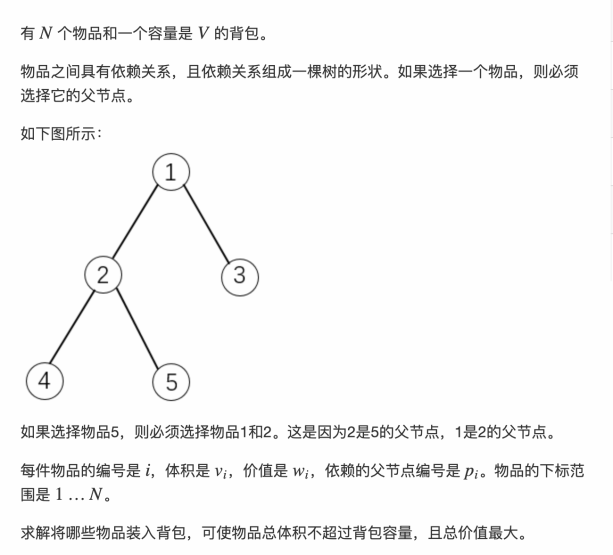
按图例节点结构所示
假如我们选择2,1也是必须要选上的;我们选择4,那么2、1节点也都要选上
反过来思考:从上往下看,首先根节点是必须选的,如果根节点不选,则说明背包过小,任何物品都放不进去。
1选了,然后在2子树和3子树做选择。看2子树或3子树是否放入,2子树可选择的情况是 {(空)、(2)、(2,4)、(2,5)、(2,4,5)},并且是从这几种情况中选择一个;以此类推,选择4子树,有两种情况{(空),(4)}
是不是和分组背包有些像,从分组里选择一个出来
当选择根节点时
从2子树和3子树(两个分组中),每个子树(分组)选择一种方案出来
当选择2节点时
从4、5子树中,每个子树选择一种方案出来
所以转换为分组背包问题
f[i][j] = max{f[i-1][j], f[i-1][j-v[0]] + w[0], ......,f[i -1][j-v[k-1]]}
i为当前选择的节点
j为当前背包容量为j
f[i][j]为当前的最优解
还有一个问题
当选2节点的时候,有这些可能性:{(空)、(2)、(2,4)、(2,5)、(2,4,5)}
这个如何构建呢,通过树的搜索算法。
选择2时的可能性 {(空),(2)}
选择4时的可能性为{(空),(4)}、选择5时的可能性为{(l空),(5)}
搜索递归的上层是根据更深的下层结果基础上计算的,所以算2的可能性时,是要把内部递归都考虑在内的,所以组合下可能性有:{(空)、(2)、(2,4)、(2,5)、(2,4,5)}
所以在考虑2时,只需要关注当层的2节点就可以了,并不需要构建2的所有可能性,2节点内部的递归就是在处理这个问题
代码实现
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N=110;
vector<int> son[N]; //用来存储每个节点的子节点
int v[N],w[N];
int f[N][N];
int n,m;
void dfs(int x){
//进行初始化,当体积小于v[x]的时候是0,大于等于v[x]的时候是w[x]
for(int j=v[x];j<=m;j++) f[x][j]=w[x];
//下面进行分组背包,从前i个子树中选,总体积不超过j的所有集合,属性max
for(int i=1;i<son[x].size();i++){
int u=son[x][i];
// 递归子节点
dfs(u);
//这里从v[x]开始,因为至少要包含x根节点,这里需要倒着枚举,因为减少了一维
for(int j=m;j>=v[x];j--){
//这里要k<=j-v[x]是因为根节点必须包含,要给根节点留空间
for(int k=0;k<=j-v[x];k++){
f[x][j]=max(f[x][j],f[x][j-k]+f[u][k]);
}
}
}
}
int main(){
cin>>n>>m;
int root;
for(int i=1;i<=n;i++) son[i].push_back(0); //将下标改成从1开始,方便后面运算
for(int i=1;i<=n;i++){
int p;
cin>>v[i]>>w[i]>>p;
if(p==-1) root=i;
else son[p].push_back(i);
}
dfs(root);
cout<<f[root][m]<<endl;
return 0;
}(该问题较难,没自己写java代码,从网上找的c的code)





















 7102
7102











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








