梯度下降基本概述

概述

梯度下降(Gradient Descent) 是机器学习中最核心的优化算法之一，其作用是通过迭代调整模型参数，逐步逼近目标函数(如损失函数)的最小值

它的数学基础是方向导数与梯度，通过负梯度方向更新参数，以最快速度降低函数值

作用

优化模型参数

在训练模型时，梯度下降通过最小值损失函数 J(θ)(如均方误差、交叉熵)，找到使预测误差最小的参数 θ (如权重 w, 偏置b)

全局/局部最优解搜索

对于凸函数（如线性回归的损失函数），梯度下降能收敛到全局最优解；对于非凸函数(如神经网络)，可能收敛到局部最优解

大规模数据高效处理

结合随机下降(SGD) 或小批量梯度下降(Mini-batch GD),梯度下降可高效处理海量数据

梯度下降的数学含义

梯度定义

梯度是一个向量，表示函数 J(θ) 在某点 θ 处增长最快的方向。数学表达式为

负梯度方向 −∇J(θ) 是函数值下降最快的方向

参数更新方式

梯度下降的更新规则为：

其中:

• η 是学习率(步长)，控制每次更新的幅度
• ∇J(θk) 是当前参数 θk 处的梯度

学习率的作用

• 太大(如 η = 1.0): 可能导致震荡甚至发散
• 太小(如 η = 0.01): 收敛速度慢，训练时间长
• 自适应调整: AdaGrad、Adam 等算法可动态调整学习率

梯度下降实例分析

案例1：简单二次函数的最小化

假设目标函数为 J(θ) = θ ^ 2, 其最小值在 θ = 0处。手动演示梯度下降的迭代过程

1. 计算梯度

2. 参数更新公式

3. 迭代过程(设初始值 θ0=3 ,学习率 η=0.1)

案例2：线性回归的参数优化

假设线性模型为 y = wx + b, 损失函数为均方误差(MSE):

其中m 是样本数量。通过梯度下降优化参数 w 和 b

1. 计算梯度

对 w 的偏导数:

对 b 的偏导数

2. 参数更新公式

3. 具体数据示例

假设训练数据如下：

真实模型 y = 2x, 初始参数 w = 0 ,b = 0, 学习率 η = 0.1

第1次迭代

1. 计算梯度
   

2. 更新参数
   

此时模型变成 y = 0.933x + 0.4。 损失值减小

第二次迭代

1. 计算新预测值
   

2. 计算梯度
   

3. 更新参数
   

经过多次迭代，w和b将逐渐逼近真实值 w = 2. b = 0

总结

1. 批量梯度下降(BGD): 使用全部数据计算梯度，计算慢但问题
2. 随机梯度下降(SGD): 每次随机选一个样本计算梯度，速度快但波动大
3. 小批量梯度下降(Mini-batch GD): 折中方案，常量批量大小 32 ~256

注意事项：

1. 学习率需合理设置（可通过网格搜索或自适应算法调整）
2. 特征标准化可加速收敛（如将输入数据缩放到均值为0，方差为1）
3. 监控损失函数曲线，判断是否收敛或过拟合

如何构造函数的梯度：详细步骤与示例

概述

梯度是多元函数在各变量方向上的偏导数组成的向量，用于描述在某点的最大增长方向及速率

构造梯度的核心是计算函数对每个自变量的偏导数

1. 梯度的数学含义

对于函数 f(x1, x2, x3, x4…, xn)， 其梯度 ∇f 为

每个分量是对应变量的偏导数，方向指向函数增长最快的方向

2. 手动构造梯度的步骤

以二元函数 f(x, y) = x ^ 2 + 3xy + y ^ 2 为例，演示梯度构造过程

1. 计算偏导数

偏导数描述的是函数在某一变量方向上的变化率，而将其他变量视为常数。具体来说

• 对x的偏导数: 固定y，仅考虑x变化时函数的变化率
• 对y的偏导数: 固定x，仅考虑y变化时函数的变化率

对 x 的偏导数
将 y 视为常数，逐项对 x 求导

1. x ^ 2 对 x 求导
   

2. 3xy 对 x 求导(y 是常数)
   

3. y^2 对x求导（y是常数，导数与x无关 ）：
   

4. 合并结果
   

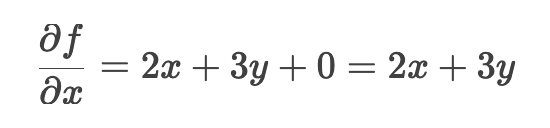
对y的偏导数
将x视为常数，逐项对y求导

1. x ^ 2 对 y 求导 (x 是常数)
   

2. 3xy 对 y求导 (x是常数)
   

3. y ^ 2 对 y求导
   

4. 合并结果
   

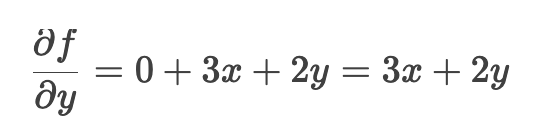
2. 构造梯度向量

案例

手动编码计算梯度

def f(x, y):
    return x**2 + 3*x*y + y**2
    
def gradient(x, y):
    df_dx = 2*x + 3*y  # 对x的偏导
    df_dy = 3*x + 2*y  # 对y的偏导
    return (df_dx, df_dy)
    

# 示例：计算点(1, 2)处的梯度
x, y = 1, 2
grad = gradient(x, y)
print(f"梯度在点({x}, {y})处为: ({grad[0]}, {grad[1]})")

结果：

梯度在点(1, 2)处为: (8, 7)

以点(1,2)为例，计算偏导数值:

1. 对 x 偏导
   

2. 对 y 偏导
   

梯度在点(1, 2)处为: (8, 7)

使用SymPy自动求导

from sympy import symbols, diff, Matrix

# 定义符号变量
x, y = symbols('x y')
f = x**2 + 3*x*y + y**2

# 计算梯度
gradient = Matrix([diff(f, x), diff(f, y)])
print("梯度表达式:")
print(gradient)

# 在点(1, 2)处代入数值
grad_at_point = gradient.subs({x: 1, y: 2})
print(f"\n点(1, 2)处的梯度: {grad_at_point}")

结果:

点(1, 2)处的梯度: Matrix([[8], [7]])

应用场景：梯度下降优化

梯度可用于寻找函数最小值。以优化问题为例，使用梯度下降法最小化 f(x,y)

import numpy as np

def f(x, y):
    return x**2 + 3*x*y + y**2

# 梯度下降参数
learning_rate = 0.1
epochs = 50
x_init, y_init = 5.0, -3.0  # 初始点

# 记录参数更新路径
path = [(x_init, y_init)]

# 执行梯度下降
x, y = x_init, y_init
for _ in range(epochs):
    df_dx = 2*x + 3*y
    df_dy = 3*x + 2*y
    x = x - learning_rate * df_dx
    y = y - learning_rate * df_dy
    path.append((x, y))
    
    
# 输出最终结果
print(f"最小值点近似值: ({x:.4f}, {y:.4f})")
print(f"函数值: {f(x, y):.4f}")

# 可视化优化路径
import matplotlib.pyplot as plt
path = np.array(path)
plt.plot(path[:, 0], path[:, 1], 'ro-', markersize=4)
plt.xlabel('x')
plt.ylabel('y')
plt.title('梯度下降路径')
plt.grid(True)
plt.show()