深蓝学院-视觉SLAM理论与实践-第十二期-第5章作业

已于 2022-03-01 01:44:26 修改
阅读量684 收藏 4
点赞数 1
分类专栏： SLAM 文章标签： 计算机视觉 opencv 自动驾驶
于 2022-02-27 22:34:22 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_40918019/article/details/123172041
版权

源代码gitee：https://gitee.com/sldwlk_admin/vslamlesson
欢迎收藏 ^ ^ 一起交流

ORB特征点

问题1：ORB提取

程序思路
  1. 判断是否在边界，如果在就跳过
  2. 计算图片在x、y方向的重心，这里要注意坐标原点时在局部图片的中心位置
  3. 用std::atan2计算重心夹角
核心代码
// compute the angle
void computeAngle(const cv::Mat &image, vector<cv::KeyPoint> &keypoints) {
  int half_patch_size = 8;
  for (auto &kp : keypoints) {
    // START YOUR CODE HERE (~7 lines)
	kp.angle = 0; 
    int cols = image.cols;
    int rows = image.rows;
	int u = kp.pt.x;
	int v = kp.pt.y;
    //边界判断
    if(u - 8 < 0 || v - 8 < 0 || u + 7 > cols - 1 || v + 7 > rows - 1)
		continue;
	//计算重心
	int m10 = 0;
	int m01 = 0;
	for(int i = u - 8; i < u + 8; i++)
	{
		for(int j = v - 8; j < v + 8; j++)
		{
			m10 += (i - u)*image.at<unsigned char>(j, i);
			m01 += (j - v)*image.at<unsigned char>(j, i);
		}
	}
    
    //计算角度
	kp.angle = std::atan2(m01, m10);
	kp.angle = kp.angle/3.1415926*180;

    
    // END YOUR CODE HERE
  }
  return;
}
CMake
find_package(OpenCV REQUIRED)
include_directories(${OpenCV_INCLUDE_DIRS})

add_executable(computeORB computeORB.cpp)
target_link_libraries(computeORB ${OpenCV_LIBRARIES})
运行结果

整体图

细节图，可以发现方向指向较亮位置

问题2：ORB描述

程序思路
  1. 计算旋转后的pq坐标
  2. 判断pq坐标是否越界
  3. 判断pq两点位置图像像素值大小设置描述符
核心代码
// compute the descriptor
void computeORBDesc(const cv::Mat &image, vector<cv::KeyPoint> &keypoints,
                    vector<DescType> &desc) {
  for (auto &kp : keypoints) {
    DescType d(256, false);
    for (int i = 0; i < 256; i++) {
      // START YOUR CODE HERE (~7 lines)
      int cols = image.cols;
      int rows = image.rows;
      float theta = kp.angle/180.0*3.1415926;
      int up = ORB_pattern[i*4 + 0];
      int vp = ORB_pattern[i*4 + 1];
      int uq = ORB_pattern[i*4 + 2];
      int vq = ORB_pattern[i*4 + 3];
      int up_ = up*cos(theta) - vp*sin(theta) + kp.pt.x;
      int vp_ = up*sin(theta) + vp*cos(theta) + kp.pt.y;
      int uq_ = uq*cos(theta) - vq*sin(theta) + kp.pt.x;
      int vq_ = uq*sin(theta) + vq*cos(theta) + kp.pt.y;
      if(up_ < 0 || up_ > cols - 1 || vp_ < 0 || vp_ > rows - 1 || uq_ < 0 || uq_ > cols - 1 || vq_ < 0 || vq_ > rows - 1)
      {
        d.clear();
        break;
      }

      if(image.at<unsigned char>(vp_, up_) - image.at<unsigned char>(vq_, uq_) < 0) 
      //前者小，记1
        d.at(i) = true;
      else
        d.at(i) = false;


      // END YOUR CODE HERE
    }
    desc.push_back(d);
  }

  int bad = 0;
  for (auto &d : desc) {
    if (d.empty())
      bad++;
  }
  cout << "bad/total: " << bad << "/" << desc.size() << endl;
  return;
}
运行结果

问题3：暴力匹配

程序思路
  1. 判断每个待查询的的描述符是否为空
  2. 为每个非空的待查询描述符遍历一遍另一个图像的所有非空描述符，得到距离最小的一个
    • 距离计算方法(汉明距离)：存在一个符号相反的二进制位，距离+1
  3. 距离如果小于阈值，则认为匹配成功，存入到结果中
核心代码
// brute-force matching
void bfMatch(const vector<DescType> &desc1, const vector<DescType> &desc2,
             vector<cv::DMatch> &matches) {
  int d_max = 50;

  // START YOUR CODE HERE (~12 lines)
  // find matches between desc1 and desc2.
  for(int i = 0; i < desc1.size(); i++)
  {
    DescType d1 = desc1[i];
    
    //判断此描述符是否为空
    if(d1.empty())
      continue;
	
    //寻找距离最短的匹配点
    int minDIst = d_max + 1;
    int minIndex; 
    for(int j = 0; j < desc2.size(); j++)
    {
      DescType d2 = desc2[j];
      int theDist = 0;
      if(d2.empty())
        continue;
      for(int i = 0; i < d1.size() && i < d2.size(); i++)
      { //计算汉明距离
        if(d1[i] != d2[i])
          theDist++;
      }
      if(theDist < minDIst)
      {
        minDIst = theDist;
        minIndex = j;
      }
        
    }
      
    //如果最小距离小于阈值，就把它加入进去
    if(minDIst <= d_max)
    {
      cv::DMatch theMatch;
      theMatch.distance = minDIst;
      theMatch.queryIdx = i;
      theMatch.trainIdx = minIndex;
      matches.push_back(theMatch);
    }

  }
  // END YOUR CODE HERE

  for (auto &m : matches) {
    cout << m.queryIdx << ", " << m.trainIdx << ", " << m.distance << endl;
  }
  return;
}
运行结果

问题4：多线程ORB

程序思路
  • 参照群里文件tbb+gcc.txt安装gcc11 g++11 tbb
  • 将原有单线程内容移植到foreach结构中
  • 对于ORB描述部分，由于多线程是无序的，因此不能使用vector的push_back函数，需要记录每个描述的关键点的index，并按位置放入到ORB描述的vector中
核心代码
//角度计算
void computeAngleMT(const cv::Mat &image, vector<cv::KeyPoint> &keypoints) {

  int half_patch_size = 8;
    
  //开启多线程，并行计算角度
  std::for_each(std::execution::par_unseq, keypoints.begin(), keypoints.end(),
                [&half_patch_size, &image](auto &kp) {
                  // START YOUR CODE HERE
                  kp.angle = 0; 

                  int cols = image.cols;
                  int rows = image.rows;
                  int u = kp.pt.x;
                  int v = kp.pt.y;
                  if(u - 8 < 0 || v - 8 < 0 || u + 7 > cols - 1 || v + 7 > rows - 1)
                  { //位于边界，直接跳过
                      
                      
                  }
                  else
                  {
                      int  m10 = 0;
                      int m01 = 0;
                      for(int i = u - 8; i < u + 8; i++)
                      {
                        for(int j = v - 8; j < v + 8; j++)
                        {
                          m10 += (i - u)*image.at<unsigned char>(j, i);
                          m01 += (j - v)*image.at<unsigned char>(j, i);
                        }
                      }
                      kp.angle = std::atan2(m01, m10);
                      kp.angle = kp.angle/3.1415926*180;
                  }
                  // END YOUR CODE HERE
                });
  return;
}

//特征描述
void computeORBDescMT(const cv::Mat &image, vector<cv::KeyPoint> &keypoints,
                      vector<DescType> &desc) {
    // START YOUR CODE HERE (~20 lines)
    //提前开辟特征描述数组容量
    desc.resize(keypoints.size());
    vector<int> kpIndexs;
    
    //记录每个特征点的下标
    for(int i = 0; i < keypoints.size(); i++)
      kpIndexs.push_back(i);
    //开启多线程，并行计算并存储特征描述
    std::for_each(std::execution::par_unseq, kpIndexs.begin(), kpIndexs.end(),
                [&desc, &image, &keypoints](auto &kpindex) {
                  // START YOUR CODE HERE
                  cv::KeyPoint kp = keypoints[kpindex];
                  DescType d(256, false);
                  //计算特征描述，保存在d中
                  for (int i = 0; i < 256; i++) {
                    int cols = image.cols;
                    int rows = image.rows;
                    float theta = kp.angle/180.0*3.1415926;
                    int up = ORB_pattern[i*4 + 0];
                    int vp = ORB_pattern[i*4 + 1];
                    int uq = ORB_pattern[i*4 + 2];
                    int vq = ORB_pattern[i*4 + 3];
                    int up_ = up*cos(theta) - vp*sin(theta) + kp.pt.x;
                    int vp_ = up*sin(theta) + vp*cos(theta) + kp.pt.y;
                    int uq_ = uq*cos(theta) - vq*sin(theta) + kp.pt.x;
                    int vq_ = uq*sin(theta) + vq*cos(theta) + kp.pt.y;
                    if(up_ < 0 || up_ > cols - 1 || vp_ < 0 || vp_ > rows - 1 || uq_ < 0 || uq_ > cols - 1 || vq_ < 0 || vq_ > rows - 1)
                    {
                      d.clear();
                      break;
                    }
                    if(image.at<unsigned char>(vp_, up_) - image.at<unsigned char>(vq_, uq_) < 0) 
                    //前者小，记1
                      d.at(i) = true;
                    else
                      d.at(i) = false;
                  }
                  //按照下标放入到数组中
                  desc[kpindex] = d;
                  // END YOUR CODE HERE
                });
    // END YOUR CODE HERE
}
运行结果

一些小问题

  1. 为什么说 ORB 是一种二进制特征？

​ 因为它的特征描述符是通过比较产生的，每一次比较对会产生一个二进制描述位(true或flase)

  1. 为什么在匹配时使用 50 作为阈值，取更大或更小值会怎么样？

​ 一共存在256个描述符，取50个作为阈值在一个合理的范围，可以过滤掉大部分误匹配，取更大的数值可能会增加误匹配的情况，取更小的数值则会减少正确的匹配数量。

  1. 暴力匹配在你的机器上表现如何？你能想到什么减少计算量的匹配方法吗？

​ 暴力匹配用时将近10s，如果图像位移不大，或者引入一个图像位姿移动的先验，降低在图片上暴力搜索的范围。

  1. 多线程版本相比单线程版本是否有提升？在你的机器上大约能提升多少性能？

​ 对于耗时较长的算法会有提升，在计算orb特征描述部分，速度提升了7倍，但是对于耗时较短的特征角度计算，速度没有提升。

从E恢复R，t

程序思路

将矩阵进行SVD分解后，按照求解公式解出R1 R2 t1 t2，任意两个Rt组合即为一组可能的解。

核心代码
#include <Eigen/Core>
#include <Eigen/SVD>
#include <Eigen/Geometry>
#include <iostream>

int main()
{
    Eigen::Matrix3d E;
    E << -0.0203618550523477, -0.4007110038118445, -0.03324074249824097 \
    , 0.3939270778216369, -0.03506401846698079, 0.5857110303721015 \
    , -0.006788487241438284, -0.5815434272915686, -0.01438258684486258;
    std::cout << "E = " << std::endl << E << std::endl;
    
    //SVD
    Eigen::JacobiSVD<Eigen::MatrixXd> svd(E, Eigen::ComputeThinU | Eigen::ComputeThinV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();
    Eigen::Matrix3d S = U.transpose()* E * V;
    std::cout << "S = " << std::endl << S << std::endl;
    //重新确定奇异值
    float s1 = (S(1,1) + S(2,2))/2;
    S << s1, 0, 0, 0, s1, 0, 0, 0, 0;
	
    //计算R1 R2 t1 t2
    Eigen::AngleAxisd rotZ(M_PI/2, Eigen::Vector3d(0, 0, 1));
    Eigen::AngleAxisd rotZ_(-M_PI/2, Eigen::Vector3d(0, 0, 1));
    Eigen::Matrix3d t1_M = U*rotZ.matrix()*S*U.transpose();
    Eigen::Matrix3d t2_M = U*rotZ_.matrix()*S*U.transpose();
    Eigen::Matrix3d R1_M = U*rotZ.matrix()*V.transpose();
    Eigen::Matrix3d R2_M = U*rotZ_.matrix()*V.transpose();
    Eigen::Vector3d t1(t1_M(2,1), - t1_M(2,0), t1_M(1,0));
    Eigen::Vector3d t2(t2_M(2,1), - t2_M(2,0), t1_M(2,0));
    std::cout << "t1 = " << std::endl << t1 << std::endl;
    std::cout << "t2 = " << std::endl << t2 << std::endl;
    std::cout << "R1 = " << std::endl << R1_M << std::endl;
    std::cout << "R2 = " << std::endl << R2_M << std::endl;
}
运行结果

使用G-N实现BA中的位姿估计

问题1：读取三维点和二维投影点

程序思路

​ 使用ifstream的>>运算符按行读取即可

核心代码
   // load points in to p3d and p2d 
    // START YOUR CODE HERE
    ifstream p2d_ifstream(p2d_file);
    ifstream p3d_ifstream(p3d_file);

    if(!p2d_ifstream.is_open() || !p3d_ifstream.is_open())
    {
        std::cout << "file open failed" << std::endl;
        return 1;
    }

    while(!p2d_ifstream.eof() && !p3d_ifstream.eof())
    {
        Eigen::Vector3d p3dSample;
        Eigen::Vector2d p2dSample;

        p2d_ifstream >> p2dSample(0) >> p2dSample(1);
        p3d_ifstream >> p3dSample(0) >> p3dSample(1) >> p3dSample(2);

        p3d.push_back(p3dSample);
        p2d.push_back(p2dSample);
    }
    // END YOUR CODE HERE
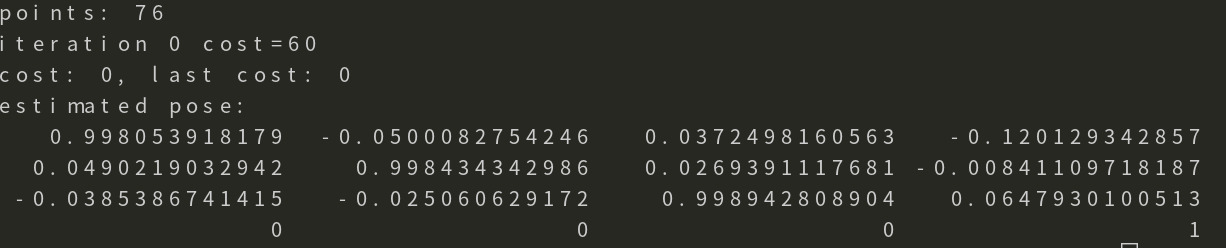
运行结果

​ 成功读取76个样本点

问题2：计算重投影误差及雅可比推导

数学推导

重投影误差： e = ∣ ∣ x − s K T c w P w ∣ ∣ e=||x-sKT_{cw}P_{w}|| e=∣∣x−sKTcw​Pw​∣∣

对模型施加左扰动，并对这个扰动求导：

核心代码
for (int i = 0; i < nPoints; i++) {
    // compute cost for p3d[I] and p2d[I]
    // START YOUR CODE HERE 
    // 计算损失
    Eigen::Vector2d e;
    Eigen::Vector2d p2d_c = p2d[i];
    Eigen::Vector3d p3d_w = p3d[i];
    Eigen::Vector3d p3d_c = T_esti*p3d_w;
    e(0) = p2d_c[0] - (fx*p3d_c[0]/p3d_c[2]+cx);
    e(1) = p2d_c[1] - (fy*p3d_c[1]/p3d_c[2]+cy);
    // END YOUR CODE HERE

    // compute jacobian
    Matrix<double, 2, 6> J;
    // START YOUR CODE HERE 
    Eigen::Matrix<double, 2, 3> J_e2Pc;
    Eigen::Matrix<double, 3, 6> J_Pc2Li;
    //重投影误差到TP的偏导
    J_e2Pc << -fx/p3d_c(2), 0, (fx*p3d_c(0))/(p3d_c(2)*p3d_c(2)), \
        0, -fy/p3d_c(2), (fy*p3d_c(1))/(p3d_c(2)*p3d_c(2));
    
    //TP到扰动李代数的偏导
    J_Pc2Li.block(0,0,3,3) = Eigen::Matrix3d::Identity(3, 3);
    J_Pc2Li.block(0,3,3,3) <<  0, p3d_c(2), -p3d_c(1), -p3d_c(2), 0, p3d_c(0), p3d_c(1), -p3d_c(0), 0; 
    //std::cout << std::endl << "J_Pc2Li = " << J_Pc2Li << std::endl;
    J = J_e2Pc*J_Pc2Li;
    // END YOUR CODE HERE

    H += J.transpose() * J;
    b += -J.transpose() * e;
}

问题3：扰动求解及李群更新

程序思路
  • 扰动求解：N-G中，由于H是半正定矩阵，因此可以采用choloesky分解的方法求解
  • 李群更新：由于采用的是左扰动模型，因此更新方式为 T = e x p ( δ Λ ) T T = exp(\delta^{\Lambda})T T=exp(δΛ)T
核心代码
// START YOUR CODE HERE 
dx = H.llt().solve(b);
// END YOUR CODE HERE

// update your estimation
// START YOUR CODE HERE 
T_esti = Sophus::SE3d::exp(dx)*T_esti;
// END YOUR CODE HERE
运行结果

一些小问题

  1. 如何定义重投影误差？

​ 重投影误差： e = ∣ ∣ x − s K T c w P w ∣ ∣ e=||x-sKT_{cw}P_{w}|| e=∣∣x−sKTcw​Pw​∣∣

  1. 该误差关于自变量的雅可比矩阵是什么？

对模型施加左扰动，并对这个扰动求导：

  1. 解出更新量之后，如何更新至之前的估计上？

由于采用的是左扰动模型，因此更新方式为 T = e x p ( δ Λ ) T T = exp(\delta^{\Lambda})T T=exp(δΛ)T

ICP实现轨迹对齐

程序思路

  1. 给每个坐标去除中心点
  2. SVD分解求R R = U V T R = UV^T R=UVT
  3. 求t t = p − R p ‘ t = p - Rp‘ t=p−Rp‘
源代码
#include <fstream>
#include <Eigen/Core>
#include <Eigen/SVD>
#include <sophus/se3.hpp>
#include <iostream>
#include <vector>
#include <pangolin/pangolin.h>
using namespace std;
void DrawTrajectory(vector<Eigen::Vector3d> points1, vector<Eigen::Vector3d> points2);
std::string filePath = "/home/sld/workspace/vslamLessonHomeWork/L5/project/data/compare.txt";
std::vector<Eigen::Vector3d> points1;
std::vector<Eigen::Vector3d> points2;
std::vector<Eigen::Vector3d> points1_;
std::vector<Eigen::Vector3d> points2_;
int main()
{
    std::ifstream file(filePath);
    if(!file.is_open())
        return 1;
    
    //数据读取
    while(!file.eof())
    {
        double time1, q11, q12, q13, q14, time2, q21, q22, q23, q24;
        Eigen::Vector3d p1;
        Eigen::Vector3d p2;
        file >> time1 >> p1[0] >> p1[1] >> p1[2] >> q11 >> q12 >> q13 >> q14 >> time2 >> p2[0]  >> p2[1]  >> p2[2]  >> q21 >> q22 >> q23 >> q24;
        points1.push_back(p1);
        points2.push_back(p2);
    }
	
    //数据点取均值
    Eigen::Vector3d p1Avg(0, 0, 0);
    Eigen::Vector3d p2Avg(0, 0, 0);
    for(int i = 0; i < points1.size(); i++)
    {
        p1Avg = p1Avg + points1[i];
        p2Avg = p2Avg + points2[i];
    }
    p1Avg = p1Avg/points1.size();
    p2Avg = p2Avg/points2.size();

    for(int i = 0; i < points1.size(); i++)
    {
        points1_.push_back(points1[i] - p1Avg);
        points2_.push_back(points2[i] - p2Avg);
    }
	
    //SVD分解求R
    Eigen::Matrix3d W;
    W << 0, 0, 0, 0, 0, 0, 0, 0, 0;
    for(int i = 0; i < points1_.size(); i++)
    {
        W = W + points1_[i]*points2_[i].transpose();
    }
	
    Eigen::JacobiSVD<Eigen::MatrixXd> svd(W, Eigen::ComputeThinU | Eigen::ComputeThinV);
    Eigen::Matrix3d U = svd.matrixU();
    Eigen::Matrix3d V = svd.matrixV();
    Eigen::Matrix3d S = U.transpose()* W * V;
    Eigen::Matrix3d R = U*V.transpose();
    //求t
    Eigen::Vector3d t = p1Avg - R*p2Avg;
	
    //坐标转换并显示
    for(int i = 0; i < points2.size(); i++)
    {
        points2[i] = R*points2[i] + t;
    }

    DrawTrajectory(points1, points2);
}
运行结果

评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值