拉格朗日乘子法和KKT 条件解析

最新推荐文章于 2024-04-30 18:18:03 发布

Wang CS

最新推荐文章于 2024-04-30 18:18:03 发布

阅读量1.3k

点赞数 2

文章标签：优化算法机器学习人工智能

本文链接：https://blog.csdn.net/weixin_41048094/article/details/94318957

版权

1.最优化问题

拉格朗日乘子法和KKT条件是求解最优化问题的重要方法，因此，在正式讲解二者之前，要先谈一谈最优化问题。

通常，需要求解的最优化问题分为3类：

1.1. 无约束优化问题:

$\min_{x}f(x)$

对于此类问题，可以通过求取优化函数的导数，使其为0即可。

1.2. 等式约束优化问题：

$\min_{x}f(x)$

$s.t.$ $h_{i}(x) = 0$ $i=1,2....m$

对于此类问题，通常利用拉格朗日乘子法，首先基于优化函数和约束条件构造拉格朗日函数，通过拉格朗日函数对各个变量求导，令导数为0，可求得候选值集合，然后验证可求最优值。具体步骤如下：

(1) 构造拉格朗日函数：

$L(x,\lambda ) = f(x)+\sum_{i=1}^{m}\lambda_{i} h_{i}(x)$

(2) 对各个变量求导并且使导数值为0：

$\triangledown_{x}L(x,\lambda) =0$

$\triangledown_{\lambda}L(x,\lambda) =0$

(3) 进行方程组联立,求解。

$\begin{cases} &\triangledown_{x}L(x,\lambda) =0 \\ & \triangledown_{\lambda}L(x,\lambda) =0 \end{cases}$

1.3.等式和不等式均有的优化问题：

$\min_{x}f(x)$

$s.t.$ $h_{i}(x) = 0$ $i=1,2....m$

$g(x)_{j}\leqslant 0$ $j=1,2....n$

对于此类问题，需要借助KKT条件，具体步骤如下：

(1) 构造拉格朗日函数：

$L(x,\lambda ) = f(x)+\sum_{i=1}^{m}\lambda_{i} h_{i}(x)+\sum_{j=1}^{n}\alpha _{j}g_{j}(x)$

(2) KKT条件：

$\begin{cases} & \triangledown _{x}L(x,\lambda,\alpha )=0 \\ & \alpha\cdot g(x)= 0 \\ & \alpha\geq 0 \end{cases}$

（3）联立KKT条件求解

$\begin{cases} & \triangledown _{x}L(x,\lambda,\alpha )=0 \\ & \alpha\cdot g(x)= 0 \\ & \alpha\geq 0 \\ &h(x)=0 \\ &g(x)\leq 0 \end{cases}$

2.拉格朗日乘子法和KKT条件能够得到最优值的原因

2.1 拉格朗日乘子法

从一个简单的二元函数来说明为什么拉格朗日乘子法works!
设定要优化的问题为：

$\min_{x}f(x) = x_{1}+x_{2}$

$s.t.$ $h(x)= x_{1}^2+x_{2}^2-2$

如图所示，斜线是目标函数的等值线，红色的圆圈代表约束条件。等值线与约束函数相交的点就是满足约束条件的点，在这些点中，需要找到使得目标函数取值最小的那个点（极值点）。这里可以直接给出一个结论：“极值点一定在等值线与约束函数曲线相切的地方取得”。因为如果在相交的地方取得，那么，沿着约束曲线往前或往后走，一定有其他相交的等值线，这样，函数会继续变大或变小，只有在切点处，继续往前和往后走，函数值才可能同时变大或变小。

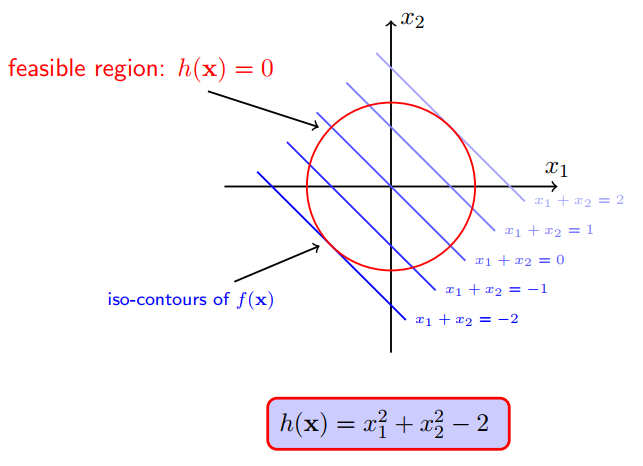
在切点处存在一个重要结论：目标函数和约束函数具有相同的切线，则相应的梯度在同一条直线上，可能是同向，也可能是反向，因为对于等式约束： $h(x)=0$ ，把 $h(x)$ 变成 $-h(x)$ 求解是一样的，但是此时梯度会反向。所以，在极小值 $x^{*}$ 处，存在如下等式：

${\color{Red} \triangledown f(x^{*}) = \lambda\triangledown h(x^{*})}$

即：

$\triangledown f(x^{*}) - \lambda\triangledown h(x^{*})=0$

此时，我们再回头看等式约束下所构造的拉格朗日函数：

$L(x,\lambda ) = f(x)+\sum_{i=1}^{m}\lambda_{i} h_{i}(x)$

对各个变量求导并且使导数值为0：

$\triangledown_{x}L(x,\lambda) =\triangledown f(x^{*})+\sum_{i=1}^{m}\lambda_{i}\triangledown h_{i}(x^*)=0$ 此式正是 $\triangledown f(x^{*}) = \lambda\triangledown h(x^{*})$ 的体现。

$\triangledown_{\lambda}L(x,\lambda) =\sum_{i=0}^{m}h_{i}(x^*)=0$ 此式正好迎合了等式约束 $h(x)=0$

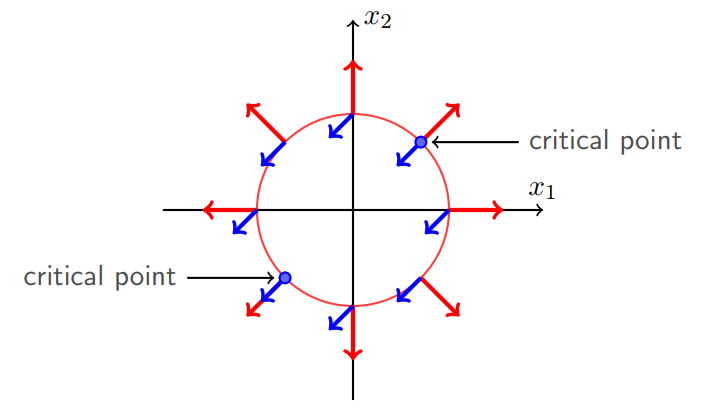
结论：综上所述，对于受等式约束的最优化问题，可以构建拉格朗日函数，并令函数对各个变量的梯度等于零，建立多个方程组，进行联立求解最优点，进而求得最优值，这种方法被称为拉格朗日乘子法，其中的 $\lambda$ 是拉格朗日乘子。

2.2 Karush-Kuhn-Tucker（KKT）条件

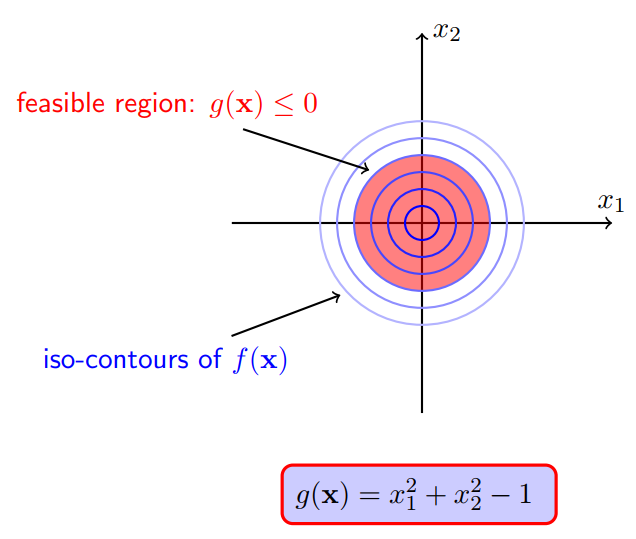
对于受不等式 $g(x)\leq 0$ 约束的最优化问题，把不等式形成的区域称为可行域。可以分两种情况对不等式约束的优化问题进行分析。

2.2.1 极值点落在可行域内（不包含边界）

考虑目标函数：

$\min_{x}f(x) = x_{1}^2+x_{2}^2$ ，

$s.t.$ $g(x) =x_{1}^2+x_{2}^2-1\leq 0$ ，

对应的拉格朗日函数：

$L(x,\lambda ) = f(x)+\sum_{j=1}^{n}\alpha _{j}g_{j}(x)$

很明显，目标函数的极值点就是原点，且该极值点在可行域内。因此，可以得出结论，如果极值点落在可行域以内，约束此时不起作用，可以像求解无约束问题一样，这时，相当于在拉格朗日函数中将系数 $\alpha$ 置零。

此时存在：

$g(x^*)<0$

$\triangledown _{x}f(x^*)=0$

对应KKT条件中的：

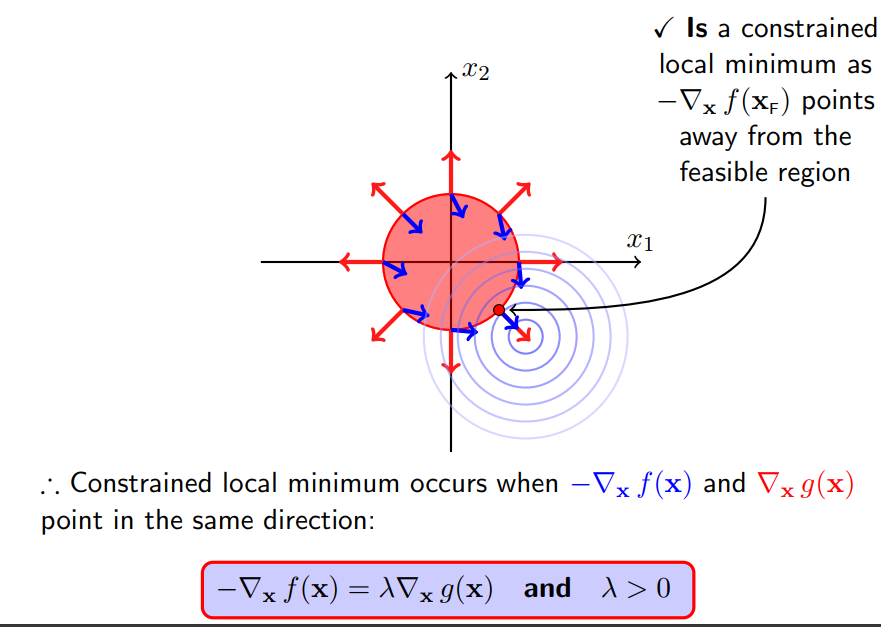
$\begin{cases} & \triangledown _{x}L(x,\alpha )=0 \\ & g(x)< 0\\ & \alpha= 0 \end{cases}$

2.2.2 极值点落在可行域外（包含边界）

目标函数：

$f(x)=(x_{1}-1.1)^2+(x_{2}+1.1)^2$

不等式约束：

$g(x) =x_{1}^2+x_{2}^2-1\leq 0$

很显然，极小值为（1.1，-1.1），落在了可行域外，这种情况下，约束起了作用，要去求解在可行域内的极小值而不是（1.1，-1.1）。对于目标函数而言，要沿着目标函数的负梯度方向，才能找到极小值，如图中蓝色箭头，这个时候约束函数的梯度往区域外发散，如图红色箭头。所以，与等式约束问题不同，在极小值点，目标函数以及约束函数的梯度反向，且极小值一定在边界上，所以有：

$g(x)=0$ 及 ${\color{Red} -\triangledown f(x^{*}) = \alpha\triangledown g(x^{*})}$ 其中， $\alpha>0$ (注意：下图中的 $\lambda$ 应该是 $\alpha$ )

对应KKT条件中的：

$\begin{cases}\ & \alpha> 0 \\ & g(x)=0 \end{cases}$

综合上述两种情况，在极值点在可行域内，有

$\begin{cases} & g(x)< 0\\ & \alpha= 0 \end{cases}$

极值点在边界上，有：

$\begin{cases}\ & \alpha> 0 \\ & g(x)=0 \end{cases}$

所以，提出第三个条件（互补松弛条件）：

$\alpha\cdot g(x)= 0$

总结以上两种情况，可以构造拉格朗日函数来转换求解问题。对于不等式约束的优化，需要满足三个条件，满足这三个条件的解x*就是极小值点。这三个条件就是著名的KKT条件，它整合了上面两种情况的条件。

$\begin{cases} & \triangledown _{x}L(x,\alpha )=0 \\ & \alpha\cdot g(x)= 0 \\ & \alpha\geq 0 \end{cases}$

特别注意：优化问题是凸优化的话，KKT条件就是极小值点（而且是全局极小）存在的充要条件。不是凸优化的话，KKT条件只是极小值点的必要条件，不是充分条件，KKT点是驻点，是可能的极值点。也就是说，就算求得的满足KKT条件的点，也不一定是极小值点，只是说极小值点一定满足KKT条件。

3.优化问题的总结

对于无约束的优化问题，直接令梯度等于0求解。

对于含有等式约束的优化问题，拉格朗日乘子法，构造拉格朗日函数，令偏导为0求解。

对于含有不等式约束的优化问题，同样构造拉格朗日函数，利用KKT条件求解。

对于含有约束的优化问题，还可以转化为对偶问题来求解。

Reference：

1. https://www.cnblogs.com/liaohuiqiang/p/7805954.html

2. https://www.cnblogs.com/WoodsWoods/p/3747274.html

Wang CS

关注

2
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
拉格朗日乘子法和KKT 条件解析

1.最优化问题拉格朗日乘子法和KKT条件是求解最优化问题的重要方法，因此，在正式讲解二者之前，要先谈一谈最优化问题。通常，需要求解的最优化问题分为3类：1.1. 无约束优化问题: 对于此类问题，可以通过求取优化函数的导数，使其为0即可。1.2. 等式约束优化问题：对于此类问题，通常利用拉格朗日乘子法，首先基于...
复制链接

扫一扫