计算机图形学线性代数基本知识
1. 向量
向量是有方向有大小的一个量
1.1 方向
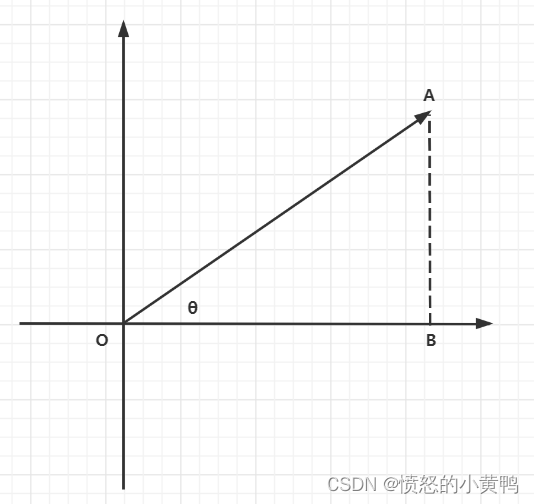
上图中假设点A为(3,2),则点A为一个标量,OA则可以用向量描述,记作
O
A
⃗
\vec{OA}
OA
向量的方向向量定义如下: 若存在向量 u ( x , y ) ,则其方向向量 w ( x ∣ u ∣ , y ∣ u ∣ ) 若存在向量u(x,y) ,则其方向向量w(\frac{x}{|u|},\frac{y}{|u|}) 若存在向量u(x,y),则其方向向量w(∣u∣x,∣u∣y)
1.2 大小
向量的大小被称之为向量的模,写作 ∣ ∣ u ⃗ ∣ ∣ ||\vec{u}|| ∣∣u∣∣。由上图可知 O A 2 = O B 2 + A B 2 {OA}^2={OB}^2+{AB}^2 OA2=OB2+AB2
1.3 向量的基本运算
1.3.1 加法

O
A
⃗
+
O
B
⃗
=
(
A
x
+
B
x
,
A
y
+
B
y
)
\vec{OA}+\vec{OB}=(A_x+B_x,A_y+B_y)
OA+OB=(Ax+Bx,Ay+By),在几何上的表现,如上图所示,将OB移动到OA的顶点,若平移后的顶点为C,则OC即为向量OA与向量OB相加的结果
1.3.2 减法
O
A
⃗
−
O
B
⃗
=
(
A
x
−
B
x
,
A
y
−
B
y
)
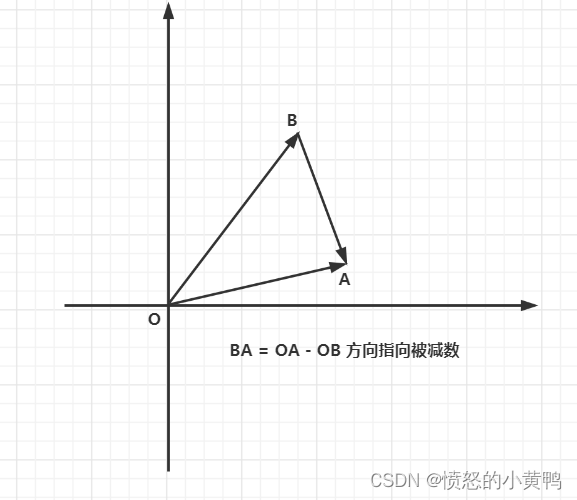
\vec{OA}-\vec{OB}=(A_x-B_x,A_y-B_y)
OA−OB=(Ax−Bx,Ay−By),在几何上的表现,如上图所示,将减数与被减数相连,且方向指向被减数,则BA即为向量OA与向量OB相减的结果
1.3.3 乘法
1.3.3.1 点乘(点积、内积、数量积)

定义OB与OA夹角为θ,且BC垂直于OA
点乘的公式:
O
A
⃗
⋅
O
B
⃗
=
∣
∣
O
A
⃗
∣
∣
⋅
∣
∣
O
B
⃗
∣
∣
c
o
s
(
θ
)
\vec{OA} · \vec{OB} = ||\vec{OA}||·||\vec{OB}||cos(θ)
OA⋅OB=∣∣OA∣∣⋅∣∣OB∣∣cos(θ)
O
A
⃗
⋅
O
B
⃗
=
A
x
⋅
B
x
+
A
y
⋅
B
y
\vec{OA} · \vec{OB} = {A_x}·{B_x} + {A_y}·{B_y}
OA⋅OB=Ax⋅Bx+Ay⋅By
点乘的几何意义,向量OA与OB的点乘可以看做是OB在OA上投影的长度
O
C
=
∣
∣
O
B
⃗
∣
∣
c
o
s
(
θ
)
OC = ||\vec{OB}||cos(θ)
OC=∣∣OB∣∣cos(θ) 与向量OA的乘积。这反映了两个向量在方向上的相似度,结果越大越相似。因此可以基于此判断,链各个向量是否垂直。
-
O
A
⃗
⋅
O
B
⃗
>
0
\vec{OA} · \vec{OB}>0
OA⋅OB>0方向基本相同,夹角在
0°到90° -
O
A
⃗
⋅
O
B
⃗
=
0
\vec{OA} · \vec{OB}=0
OA⋅OB=0相互垂直 ,夹角为
90° -
O
A
⃗
⋅
O
B
⃗
=
0
\vec{OA} · \vec{OB}=0
OA⋅OB=0方向基本相反 ,夹角在
90°到180°之间
参考
1.3.3.2 叉乘(向量积)
有关叉乘个人觉得【回归本源】1.3-向量叉乘这篇介绍蛮不错的,这里简单概述下结论。算是记录下:
- 叉乘的计算公式
v ⃗ ⋅ u ⃗ = ( v y ⃗ u z ⃗ − v z ⃗ u y ⃗ v z ⃗ u x ⃗ − v x ⃗ u z ⃗ v x ⃗ u y ⃗ − v y ⃗ u x ⃗ ) \vec{v}·\vec{u} = \left( \begin{array}{} \vec{v_y}\vec{u_z} - \vec{v_z}\vec{u_y}\\ \vec{v_z}\vec{u_x} - \vec{v_x}\vec{u_z}\\ \vec{v_x}\vec{u_y} - \vec{v_y}\vec{u_x}\end{array}\right) v⋅u=⎝ ⎛vyuz−vzuyvzux−vxuzvxuy−vyux⎠ ⎞
∣ v ⃗ ⋅ u ⃗ ∣ = ∣ v ⃗ ∣ ⋅ ∣ u ⃗ ∣ s i n ( θ ) |\vec{v}·\vec{u}|=|\vec{v}|·|\vec{u}|sin(θ) ∣v⋅u∣=∣v∣⋅∣u∣sin(θ) - 几何意义
叉乘的结果在几何上表示,垂直于$\vec{v}\vec{u}$平面的法向量
通常情况下,向量的叉乘公式比较难记,可以借助3阶行列式计算方式进行记忆,如下:
v
⃗
⋅
u
⃗
=
∣
i
⃗
j
⃗
k
⃗
v
x
v
y
v
z
u
x
u
y
u
z
∣
=
(
v
y
u
z
−
v
z
u
y
)
i
⃗
+
(
v
z
u
x
−
v
x
u
z
)
j
⃗
+
(
v
x
u
y
−
v
y
u
x
)
k
⃗
\vec{v}·\vec{u}= \begin{vmatrix} \vec{i}&\vec{j}&\vec{k}\\ v_x&v_y&v_z\\ u_x&u_y&u_z \end{vmatrix}=(v_yu_z-v_zu_y)\vec{i}+(v_zu_x-v_xu_z)\vec{j}+(v_xu_y-v_yu_x)\vec{k}
v⋅u=∣
∣ivxuxjvyuykvzuz∣
∣=(vyuz−vzuy)i+(vzux−vxuz)j+(vxuy−vyux)k
其中
i
⃗
=
(
1
0
0
)
\vec{i}=\left(\begin{array}{}1\\0\\0\end{array}\right)
i=⎝
⎛100⎠
⎞、
j
⃗
=
(
0
1
0
)
\vec{j}=\left(\begin{array}{}0\\1\\0\end{array}\right)
j=⎝
⎛010⎠
⎞、
k
⃗
=
(
0
0
1
)
\vec{k}=\left(\begin{array}{}0\\0\\1\end{array}\right)
k=⎝
⎛001⎠
⎞。观察其表达式可发现,叉乘的计算公式就是,小括号中的内容。
用矩阵则表示如下:
v
⃗
⋅
u
⃗
=
[
0
−
v
z
v
y
v
z
0
−
v
x
−
v
y
v
x
0
]
[
u
x
u
y
u
z
]
\vec{v}·\vec{u}= \begin{bmatrix} 0&-v_z&v_y\\ v_z&0&-v_x\\ -v_y&v_x&0 \end{bmatrix} \begin{bmatrix} u_x\\ u_y\\ u_z \end{bmatrix}
v⋅u=⎣
⎡0vz−vy−vz0vxvy−vx0⎦
⎤⎣
⎡uxuyuz⎦
⎤
参考
2. 矩阵
2.1 矩阵的本运算
- 矩阵的乘法
[ a 11 a 12 a 13 a 14 a 21 a 22 a 23 a 24 a 31 a 32 a 33 a 34 a 41 a 42 a 43 a 44 ] ⋅ [ b 11 b 12 b 21 b 22 b 31 b 32 b 41 b 42 ] = [ a 11 b 11 + a 12 b 21 + a 13 b 31 + a 14 b 41 a 11 b 12 + a 12 b 22 + a 13 b 32 + a 14 b 42 a 21 b 21 + a 22 b 21 + a 23 b 31 + a 24 b 41 a 21 b 22 + a 22 b 22 + a 23 b 32 + a 24 b 42 a 31 b 31 + a 32 b 21 + a 33 b 31 + a 34 b 41 a 31 b 32 + a 32 b 22 + a 33 b 32 + a 34 b 42 a 41 b 41 + a 42 b 21 + a 43 b 31 + a 44 b 41 a 41 b 42 + a 42 b 22 + a 43 b 32 + a 44 b 42 ] \begin{bmatrix} a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{33}&a_{34}\\ a_{41}&a_{42}&a_{43}&a_{44} \end{bmatrix} · \begin{bmatrix} b_{11}&b_{12}\\ b_{21}&b_{22}\\ b_{31}&b_{32}\\ b_{41}&b_{42} \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31}+a_{14}b_{41}&a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32}+a_{14}b_{42}\\ a_{21}b_{21} + a_{22}b_{21} + a_{23}b_{31}+a_{24}b_{41}&a_{21}b_{22} + a_{22}b_{22} + a_{23}b_{32}+a_{24}b_{42}\\ a_{31}b_{31} + a_{32}b_{21} + a_{33}b_{31}+a_{34}b_{41}&a_{31}b_{32} + a_{32}b_{22} + a_{33}b_{32}+a_{34}b_{42}\\ a_{41}b_{41} + a_{42}b_{21} + a_{43}b_{31}+a_{44}b_{41}&a_{41}b_{42} + a_{42}b_{22} + a_{43}b_{32}+a_{44}b_{42} \end{bmatrix} ⎣ ⎡a11a21a31a41a12a22a32a42a13a23a33a43a14a24a34a44⎦ ⎤⋅⎣ ⎡b11b21b31b41b12b22b32b42⎦ ⎤=⎣ ⎡a11b11+a12b21+a13b31+a14b41a21b21+a22b21+a23b31+a24b41a31b31+a32b21+a33b31+a34b41a41b41+a42b21+a43b31+a44b41a11b12+a12b22+a13b32+a14b42a21b22+a22b22+a23b32+a24b42a31b32+a32b22+a33b32+a34b42a41b42+a42b22+a43b32+a44b42⎦ ⎤
矩阵乘法中矩阵 A m × n A_{m×n} Am×n与矩阵 B k × l B_{k×l} Bk×l的n和k必须相等,其中mn和kl分别表示矩阵的行列数。最后的结果矩阵为 R m × l R_{m×l} Rm×l,可以看出结果矩阵的一个元素 R m l R_{ml} Rml就等于矩阵 A A A的第 m m m行与矩阵 B B B的第 l l l列对应元素分别相乘再相加的结果。 - 矩阵加/减法
[ a 11 a 12 a 13 a 21 a 22 a 23 ] ± [ b 11 b 12 b 13 b 21 b 22 b 23 ] = [ a 11 ± b 11 a 12 ± b 12 a 13 ± b 13 a 21 ± b 21 a 22 ± b 22 a 23 ± b 23 ] \begin{bmatrix} a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23} \end{bmatrix} \pm \begin{bmatrix} b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23} \end{bmatrix}= \begin{bmatrix} a_{11}\pm b_{11}&a_{12}\pm b_{12}&a_{13}\pm b_{13}\\ a_{21}\pm b_{21}&a_{22}\pm b_{22}&a_{23}\pm b_{23} \end{bmatrix} [a11a21a12a22a13a23]±[b11b21b12b22b13b23]=[a11±b11a21±b21a12±b12a22±b22a13±b13a23±b23]
矩阵加法或减法时矩阵的行列数必须相等
2.2 缩放
[ S 1 0 0 0 0 S 2 0 0 0 0 S 3 0 0 0 0 1 ] ⋅ [ x y z 1 ] = [ S 1 x S 2 y S 3 z 1 ] \begin{bmatrix} S_1&0&0&0 \\ 0&S_2&0&0 \\ 0&0&S_3&0 \\ 0&0&0&1 \end{bmatrix} · \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}= \begin{bmatrix} S_1x\\ S_2y\\ S_3z\\ 1 \end{bmatrix} ⎣ ⎡S10000S20000S300001⎦ ⎤⋅⎣ ⎡xyz1⎦ ⎤=⎣ ⎡S1xS2yS3z1⎦ ⎤
2.3 位移
[ 1 0 0 T x 0 1 0 T y 0 0 1 T z 0 0 0 1 ] ⋅ [ x y z 1 ] = [ x + T x y + T y z + T z 1 ] \begin{bmatrix} 1&0&0&T_x \\ 0&1&0&T_y \\ 0&0&1&T_z \\ 0&0&0&1 \end{bmatrix} · \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}= \begin{bmatrix} x+T_x\\ y+T_y\\ z+T_z\\ 1 \end{bmatrix} ⎣ ⎡100001000010TxTyTz1⎦ ⎤⋅⎣ ⎡xyz1⎦ ⎤=⎣ ⎡x+Txy+Tyz+Tz1⎦ ⎤
2.4 关于齐次坐标的解释
在缩放和位移矩阵中,可以看到明明是三维的(x,y,z)缺用四维矩阵和向量来表示和计算。
仔细观察位移的计算过程中如果使用三维的矩阵和向量来计算应该怎么处理?会发现好像很难处理甚至是不能处理,这个时候引入的解决方案就是齐次坐标,关于齐次坐标的核心介绍如下
齐次坐标是用N+1个维来表示N维坐标的一种方式,在计算机图形学中非常重要
如果一个向量的齐次坐标是0,这个坐标就是方向向量,这个向量是不能够位移的
2.5 旋转
关于旋转中角度与弧度的关系:
- 角度 = 弧度 * (180°/PI)
- 弧度 = 角度 * (PI /180°)
以下公式基于左手坐标系
- 绕X轴旋转
[ 1 0 0 0 0 c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 ] ⋅ [ x y z 1 ] = [ x c o s θ ⋅ y − s i n θ ⋅ z s i n θ ⋅ y + c o s θ ⋅ z 1 ] \begin{bmatrix} 1&0&0&0\\ 0&cosθ&-sinθ&0\\ 0&sinθ&cosθ&0\\ 0&0&0&1 \end{bmatrix} · \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} x\\ cosθ·y - sinθ·z\\ sinθ·y + cosθ·z\\ 1 \end{bmatrix} ⎣ ⎡10000cosθsinθ00−sinθcosθ00001⎦ ⎤⋅⎣ ⎡xyz1⎦ ⎤=⎣ ⎡xcosθ⋅y−sinθ⋅zsinθ⋅y+cosθ⋅z1⎦ ⎤ - 绕Y轴旋转
[ c o s θ 0 s i n θ 0 0 1 0 0 − s i n θ 0 c o s θ 0 0 0 0 1 ] ⋅ [ x y z 1 ] = [ c o s θ ⋅ x + s i n θ ⋅ z y − s i n θ ⋅ x + c o s θ ⋅ z 1 ] \begin{bmatrix} cosθ&0&sinθ&0\\ 0&1&0&0\\ -sinθ&0&cosθ&0\\ 0&0&0&1 \end{bmatrix} · \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} cosθ·x + sinθ·z\\ y\\ -sinθ·x + cosθ·z\\ 1 \end{bmatrix} ⎣ ⎡cosθ0−sinθ00100sinθ0cosθ00001⎦ ⎤⋅⎣ ⎡xyz1⎦ ⎤=⎣ ⎡cosθ⋅x+sinθ⋅zy−sinθ⋅x+cosθ⋅z1⎦ ⎤ - 绕Z轴旋转
[ c o s θ − s i n θ 0 0 s i n θ c o s θ 0 0 0 0 1 0 0 0 0 1 ] ⋅ [ x y z 1 ] = [ c o s θ ⋅ x − s i n θ ⋅ y s i n θ ⋅ x + c o s θ ⋅ y z 1 ] \begin{bmatrix} cosθ&-sinθ&0&0\\ sinθ&cosθ&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{bmatrix} · \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} cosθ·x - sinθ·y\\ sinθ·x + cosθ·y\\ z\\ 1 \end{bmatrix} ⎣ ⎡cosθsinθ00−sinθcosθ0000100001⎦ ⎤⋅⎣ ⎡xyz1⎦ ⎤=⎣ ⎡cosθ⋅x−sinθ⋅ysinθ⋅x+cosθ⋅yz1⎦ ⎤ - 绕任意轴旋转
[ c o s θ + R x 2 ( 1 − c o s θ ) R x R y ( 1 − c o s θ ) − R z s i n θ R x R z ( 1 − c o s θ ) + R y s i n θ 0 R y R x ( 1 − c o s θ ) + R z s i n θ c o s θ + R y 2 ( 1 − c o s θ ) R y R z ( 1 − c o s θ ) − R x s i n θ 0 R z R x ( 1 − c o s θ ) − R y s i n θ R z R y ( 1 − c o s θ ) + R x s i n θ c o s θ + R z 2 ( 1 − c o s θ ) 0 0 0 0 1 ] \begin{bmatrix} cosθ+{R_x}^2(1-cosθ)&R_xR_y(1-cosθ)-R_zsinθ&R_xR_z(1-cosθ)+R_ysinθ&0\\ R_yR_x(1-cosθ)+R_zsinθ&cosθ+{R_y}^2(1-cosθ)&R_yR_z(1-cosθ)-R_xsinθ&0\\ R_zR_x(1-cosθ)-R_ysinθ&R_zR_y(1-cosθ)+R_xsinθ&cosθ+{R_z}^2(1-cosθ)&0\\ 0&0&0&1 \end{bmatrix} ⎣ ⎡cosθ+Rx2(1−cosθ)RyRx(1−cosθ)+RzsinθRzRx(1−cosθ)−Rysinθ0RxRy(1−cosθ)−Rzsinθcosθ+Ry2(1−cosθ)RzRy(1−cosθ)+Rxsinθ0RxRz(1−cosθ)+RysinθRyRz(1−cosθ)−Rxsinθcosθ+Rz2(1−cosθ)00001⎦ ⎤
其中 R R R为单位化的旋转轴
常见的旋转表述方式还有欧拉角、四元数






















 761
761











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








