Bayesian Flow Networks（BFN）合集3

这里与大家探探 BFN 在面对离散化数据时是怎么玩的，详解离散化数据概念以及实现离散化过程。详解贝叶斯流网络在离散化数据场景下的实现

前面解析了 BFN 在连续(continuous)数据场景下的具体实现后，本文紧接着来与大家探探 BFN 在面对离散化数据时是怎么玩的。离散化数据是比较有个性的，虽然它是个名词，但其实蕴含着一个过程，具有动词的属性。具体如何，接下来会在正文中详细说到。

本文会首先介绍离散化数据的概念，并进一步列出其与最易混淆的离散数据之间的区别；接着，CW 会介绍作者是如何对数据实现离散化的，同时一并介绍其在离散化数据场景下的一些框架设置；然后，就开始步入正题—— BFN 在离散化数据场景下的数学实现；最后谈了谈离散化可能产生的利弊 和 BFN 在此场景下实现的伪代码。另外，和前面的文章一样，关于文中所引用到的数学结论的证明，CW 都放在附录中了，感兴趣的可以扫一扫~

什么是离散化(discretised)数据

何谓离散化数据？这名字可能会有误导性，让你下意识以为它是离散型(discrete)数据。然而，离散化数据的意思是将连续型(continuous)数据转换为离散型数据的过程或结果，其中隐含着一个转换过程。通常可以将连续数值划分为多个等长的数值区间，然后将位于同一区间内的连续数值都使用同一个离散数值(或类别)来表示。

离散化数据 vs 离散数据

为了让大家更清楚地了解离散化数据，CW 觉得有必要在此列举一下它与离散化数据的区别：

• 离散数据是数据的一种类型，而离散化数据更多地代表着数据的一种处理方式；
• 离散数据它本身就长那样，不是由某某转换而来；而离散化数据的“根”是连续数据、是可还原的；
• 离散数据的数值只能是整数，而离散化数据的数值可以是任意的。

如何实现离散化

(你看, 是不是真的可以考虑让你们上中学的弟弟妹妹教你。你也不用怕丢脸, 待他/她答出来后你就说这是你故意考他/她的)

在离散化场景下的一些设置

由于离散化数据就是在原本连续数值的基础上划分区间，因此 BFN 在离散化场景下的实现大多沿用了在连续数据场景下的实现，主要的不同在于对输出分布进行了离散化，而输入分布、发送者分布仍保持为连续的。

作者说之所以这样选择，一方面是因为数学上更易实现(贝叶斯更新面对离散化的分布会很复杂)，另一方面是他觉得 BFN 以连续的输入分布参数作为输入会更好地“消化与吸收”，相比于以离散的概率值作为输入会更易学到数据的规律。

输出分布

如果把 BFN 在离散化数据场景下的实现看作是一首歌，那么其中的副歌部分(通常是一首歌的高潮部分)就是输出分布，因为其余部分的实现都直接“白嫖”自连续型数据场景。

在上一篇文章中，你们已经了解到：在连续型数据场景下，输出分布被建模为单点分布。而在本文的离散化数据场景中，数据的表示被分割为有限个数值区间，所有的数值可能性都被“囊括”在这些区间里，每个连续值都唯一地属于一个区间，属于同一个区间的连续值都会被无差别对待，相当于对连续值进行了分类，每个区间就代表一个类别。所以输出分布理应为每个区间都赋予一定概率，于是就建模为 分类分布(categorical distribution)。

OK，了解大体思想后，现在来讲下具体做法。

以上结果是网络对于原来连续(离散化之前)数据分布的估计，它依然是连续的高斯分布，而我们的目标是能够输出各区间概率的离散型分布。那么兄弟们，该如何完成 KPI 呢？

可以这么考虑：每个区间都有左右两个端点，对于上面估计出来的连续型分布，将数据小于等于右端点的概率减去小于等于左端点的概率，就得到了位于左右端点之间的概率，也就是位于对应区间内的概率。

而在分布中，小于等于某点的概率可以用 累积分布函数(CDF) 来表示，于是输出分布赋予某个区间的概率就是：网络估计出来的(连续型)分布的累积分布函数在对应区间右端点的函数值减去在左端点的函数值。

(具体推导过程请见附录)

以下展示的是将网络估计出来的连续型分布离散化至各区间概率的示意图。可以看到，由于前面提到的对 CDF 的截断操作，原本连续型分布的长尾部分都被集中在首尾区间，因此首尾区间的概率会有不服从于原来连续曲线的现象。

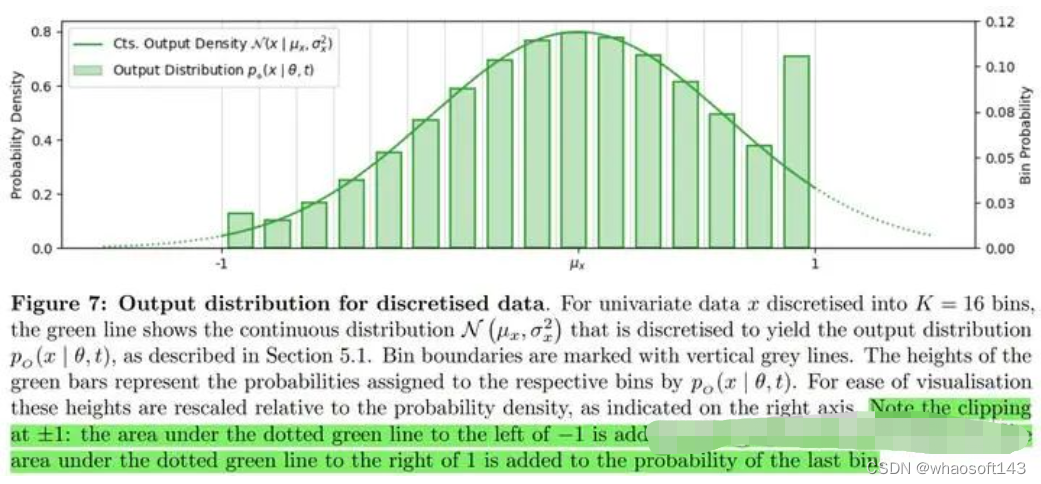
接收者分布

接收者分布中的数据由采样自输出分布的数据加噪而来，加噪方式如同发送者分布，于是接收者分布就是发送者分布在输出分布上的期望(有疑惑的请复习本系列前面两篇文章)。

由此可知，接收者分布依然是连续型分布，而且它在每一维实质上是 混合高斯分布(GMM)。

重构损失

与上一篇文章的连续数据不同，在这里，数据是离散化的，重构它不会存在“无限精度”的问题(具体可回顾上一篇文章中“重构损失”那章)。于是，重构损失就如本系列首篇文章中所说的，是：最后时刻的负对数似然在贝叶斯流分布上的期望：

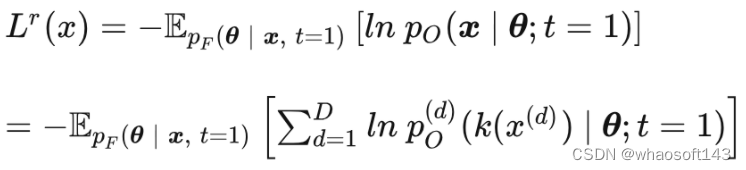
同样，与前面几篇文章中所说的一样，重构损失是不用于训练的。

离散时间的损失函数

也就是说，在计算发送者分布和接收者分布之间的 KL 散度时，先从发送者分布中采样，然后再利用采样结果去计算两者的对数概率密度差(根据定义，发送者分布和接收者分布的 KL 散度就是它们的对数概率密度差在发送者分布上的期望)。

连续时间的损失函数

在本系列的首篇文章中已说过，在连续时间的情况下，作者提出发送者分布和接收者分布之间的 KL 散度拥有以下泛化形式：

“福利”与“麻烦”

关于 BFN 在离散化数据场景的主要实现 CW 已经基本讲完了，现在我们不妨来思考下离散化有什么好处或不便，想一想离散化操作有没有为网络的训练和性能带来福利或麻烦。

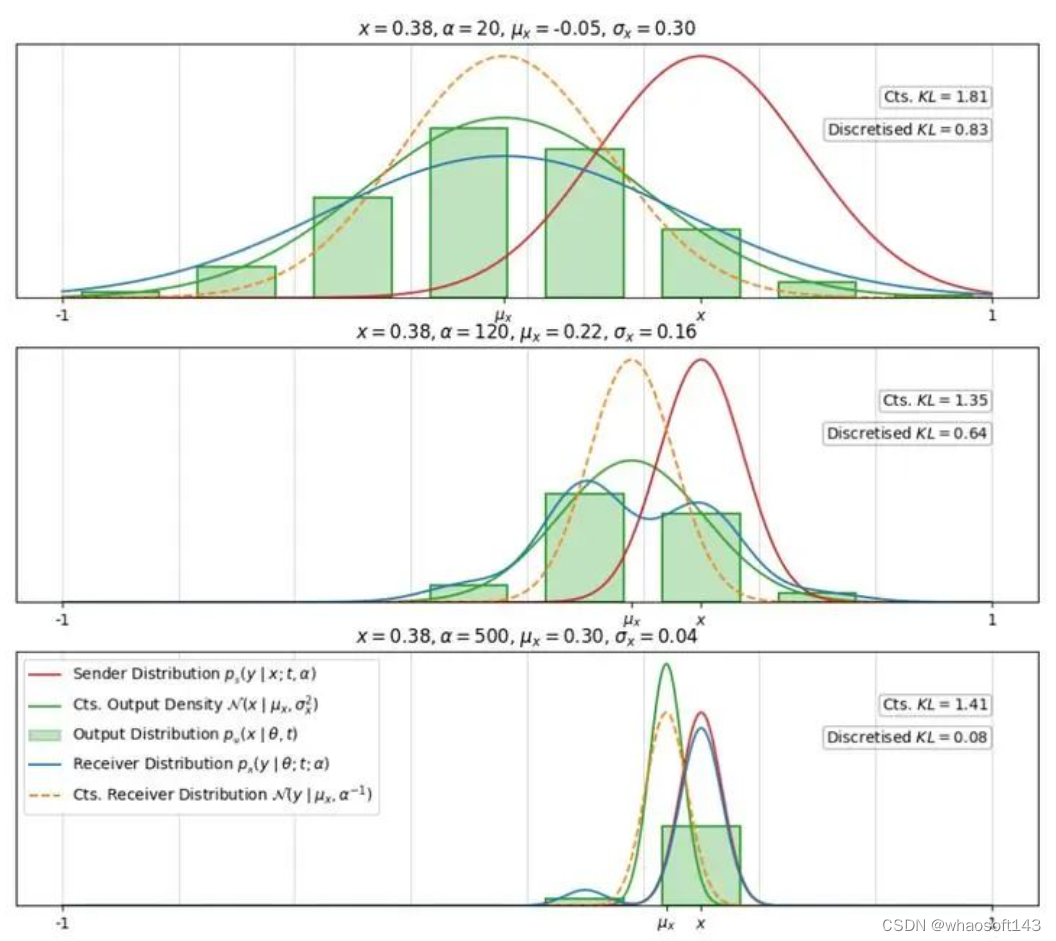
上图的红色曲线代表发送者分布、绿色曲线代表网络估计的连续分布、绿色柱状条代表其经过离散化后的输出分布、蓝色曲线是对应的接收者分布，而橙色虚曲线是在原来网络估计出的连续分布上加噪而形成的接收者分布。

注意，以上图示的数据是已经过离散化的。从中可以看出，发送者分布和在离散化的输出分布基础上形成的接收者分布之间的 KL 散度，比起连续的接收者分布之间的会更小。 这是因为，离散化会将一段范围内的连续值都“集中”至一点，相对没有那么“发散”，在网络训练得当的情况下，会使得接收者分布更“靠近”发送者分布，因为在这里，数据已经过离散化。

由此可以大致推测，与连续数据场景下相比，在离散化的情况下，接收者分布通常更易拟合发送者分布，因为离散化的数据更为“集中”，而连续数据实际上是不可能“定位”至具体某点的。

随着 KKK 的增加，计算复杂度会随之变高，但同时数据的表示精度又会更加精确(区间的长度越小，越接近于连续数据)，从这个角度看，又有点博弈的味道~

伪代码

前面都是在吹水，是时候给点真材实料了！这样才能让大家看到实操的可能性。虽然所谓的真材实料在这里其实也不是实打实的，毕竟是“伪”代码，但起码也是能给到你们一些实际感，相对不会那么空洞。

离散化的累积分布函数

CDF 没啥好说的，对照前文解释即可秒懂，就酱~

首先根据输出分布计算出从第一个区间至最后一个的累积概率，然後使用随机数生成算法生成一個 0~1 的随机数，看这个数落在哪个累积概率区间，最终就以对应区间的索引作为采样结果。

另外，如上一篇文章中所述：在推理过程中，由于每一步网络生成的样本都是变化的，因此需要显式地根据当前的生成结果来构造观测样本，从而实现贝叶斯(后验)更新(而不能像训练时那样直接通过贝叶斯流分布实现)。

附：标准正态分布的累积分布函数与误差函数之间的关系推导

在这部分，CW 就和大家一起齐心协力(配合下嘛~)地推导下如何通过误差函数 erf 来计算标准正态分布的 CDF。

首先，明确下误差函数的数学定义：

或许你们会好奇到：误差函数 erf 的值又该如何计算呢？毕竟它也没有解析形式。

OK，那么 CW 就顺带将这个问题也展开讲一下(又能愉快地吹水了，耶~！)。

误差函数 erf 的计算方法有多种，常见的有采用 数值方法 来近似计算。在这里，CW 介绍下另一种——使用 泰勒展开式 来近似计算。

如果照这么玩下去，你会发现：

现在, 将上述结果代入到泰勒展开式中, 最终得到:

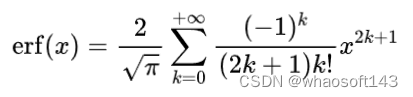
至于上式具体要展开到多少阶，就取决于你的心情了~

原创作者: whaosoft 转载于: https://blog.51cto.com/whaosoft/11638022