矩阵分解技术

矩阵分解技术是一种将一个复杂矩阵分解为若干更简单、更易于处理的矩阵的方法。这种技术在现代科学和工程领域中扮演着重要角色，尤其是在数据分析、机器学习、信号处理等领域中具有广泛应用。

常见的矩阵分解方法

1. 特征值分解（EVD） ：适用于方阵，通过将矩阵分解为特征向量和特征值的集合，可以用于数据压缩和降维。
   

2. 奇异值分解（SVD） ：适用于任何矩阵，将矩阵分解为三个正交矩阵的乘积，即 $ A = UΣV^T $，其中 $ U $ 和 $ V $ 是正交矩阵，$ Σ $ 是对角矩阵。SVD在数据压缩、图像处理和推荐系统中应用广泛。
   

3. QR分解：将矩阵分解为一个正交矩阵 $ Q $ 和一个上三角矩阵 $ R $，适用于求解线性方程组和最小二乘问题。
   

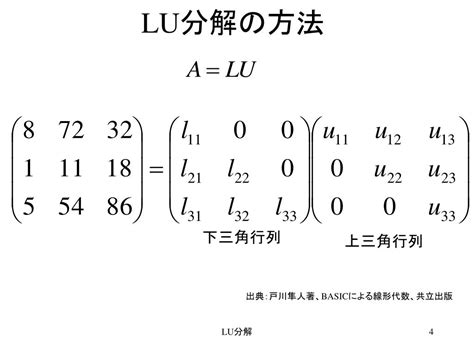
4. LU分解：将矩阵分解为一个下三角矩阵 $ L $ 和一个上三角矩阵 $ U $，常用于解线性方程组和计算矩阵的逆。
   

5. 非负矩阵分解（NMF） ：将矩阵分解为两个非负矩阵的乘积，常用于数据降维和特征提取。
   

矩阵分解的应用

• 推荐系统：通过矩阵分解，可以预测用户对物品的评分，从而实现个性化推荐。